L'urée,
Concours interne ingénieur de l'industrie et des mines 2017 .
|
|
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
L'urée ( (NH 2) 2CO est soluble danqs l'eau à hauteur de 119 g pour 100 g d'eau à 25°C. A. Structure.
A.1. Donner la formule de Lewis de l'urée. Justifier la bonne solubilité de l'urée dans l'eau.
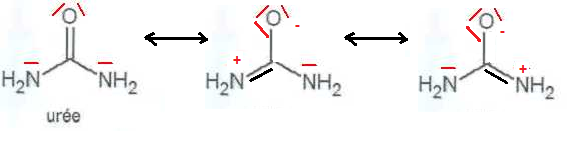
L'urée, molécule polaire, est soluble dans un solvant polaire, comme l'eau.
A.2. Quelle est la
valeur de l'enthalpie de formation de l'urée solide dans les conditions
standard, que l'on peut calculer en utilisant la loi de Hess ?
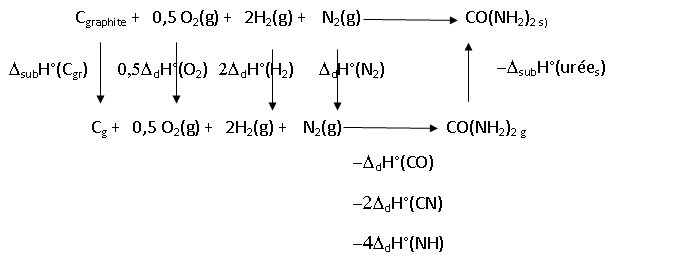 Df
DfH°(urée(s)) = DsubH°(C(gr)) +0,5 DdH°(O2)+2 DdH°(H2) + DdH°(N2) - DdH°(CO)- 2DdH°(CN)-4 DdH°(NH)-DsubH°(urée(s)).
DfH°(urée)=720 +0,5 x494 +2 x431 +946 -735-2 x293-4x389-110 = -212 kJ / mol.
A.3. L'enthalpie de
formation de l'urée solide est -333,2 kJ / mol. Quelle raison
structurelle explique la différence avec la valeur calculée ?
Le
calcul à partir des énergies de liaisons ne prend pas en compte
l'énergie de résonance créée par la délocalisation électronique.
B. Synthèse de l'urée.
2NH3(g) +CO2(g) = OC(NH2)2 (s) +H2O(l). R.
B.1. Calculer l'enthalpie standard ainsi que l'entropie standard de la réaction (R) à 298°K et commenter les signes obtenus.
DrH° =DfH°(urée(s)) +DfH°(H2O(l))-DfH°(CO2(g))-2 DfH°(NH3(g)).
DrH° = -333,2 +(-285,8) -(-393,5) -2 x(-46,1) = -133,3 kJ / mol.
Cette valeur étant négative, la réaction est exothermique.
DrS° =S°(urée(s)) +S°(H2O(l))-S°(CO2(g))-2 S°(NH3(g)).
DrS° = 104,6 +69,9 -213,6 -2 x192,3 = -423,7 J / mol.
Il y a trois molécules de gaz parmi les réactifs et un solide + un liquide parmi les produits.
Le désordre diminue au cours de la réaction, il y a baisse de l'entropie ( ce qui se traduit par le signe négatif).
Ces deux valeurs seront supposées constantes sur l'intervalle de température [280 K ; 350 K].
|
....
.....
|
B.2. Calculer l'enthalpie libre standard de la réaction à 298 K et en déduire la constante d'équilibre correspondante.
DrG° =DrH° -T DrS° = -133,3 -298 (-0,4237) = -7,04 kJ /mol.
DrG° = -RT ln K ; ln K = 7,04 103 /(8,31 x298) =2,8.
K = 16,4
B.3. Calculer la température d'inversion Ti, température pour laquelle DrG° est nulle. Quel est l'effet d'une augmentation de température sur l'équilibre étudié ?
-133,3 -Ti (-0,4237) =0 ; Ti = 133,3 /0,4237 ~315 K.
La réaction étant exothermique, à pression constante, une augmentation de température déplace l'équilibre dans le sens indirect.
On part d'un mélange contenant initialement 5 moles d'ammoniac et 2 moles de dioxyde de carbone à 323 K.
B.4. Calculer la constante d'équilibre à 323 K.
DrG° =DrH° -T DrS° = -133,3 -323 (-0,4237) = 3,55 kJ /mol.
DrG° = -RT ln K ; ln K = -3,55 103 /(8,31 x323) =-1,32.
K = 0,267.
B.5. Exprimer cette
constante d'équilibre en fonction de l'avancement de la réaction x et
de la pression totale P. En déduire la pression initiale du mélange
pour obtenir un rendement de 90 %.
Etat
|
Avancement (mol)
|
2NH3(g) |
+CO2(g) |
= OC(NH2)2 (s) |
+H2O(l). |
initial
|
0
|
5
|
2
|
0
|
0
|
final
|
x
|
5-2x
|
2-x
|
x
|
x
|
Nombre total de moles : 5-2x +2-x = 7-3x.
Pression partielle de l'ammoniac PNH3 = (5-2x) / (7-3x) P.
Pression partielle de CO2 : PCO2 = (2-x) / (7-3x) P.
K=1 / (P2NH3 PCO2) =(7-3x)3 / ((5-2x)(2-x)P3).
Rendement 90 % : x = 2 x0,9 =1,8 ; 0,267 = (7-3 *1,8)3 / ((5-2*1,8)(2-1,8)P3).
0,267 = 4,0967 / (1,4*0,2 P3).
P3 =14,63 / 0,267 = 54,79 ; P ~3,8 bar.
..
|
|
|
C. Décomposition de l'urée dans l'eau.
Vers 80°C, l'urée se décompose dans l'eau via l'ion cyanate en ammonium et CO2 selon :
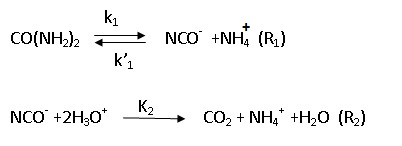
C.1. Exprimer la vitesse de formation de CO2 en fonction des concentrations en urée (notée u), en ammonium ( noté n) et en H+ ( noté h).
v = d[CO2] / dt = k2 [NCO-] [H3O+]2 = k2 [NCO-] h2 .
Approximation d'état quasi-stationnaire appliquée au cyanate :
d[NCO-] / dt = 0 = k1 u - k'1[NCO-] [NH4+] - k2 [NCO-] h2 .
[NCO-] = k1 u / ( k'1 [NH4+] + k2 h2 ).
v = k2 k1 u h2 / ( k'1 [NH4+] + k2 h2 ) .
v = k2 k1 u h2 / ( k'1 n + k2 h2 ) .
|
|
|
|
Dans
un réacteur fermé, on chauffe 950 mL d'une solution de chlorure
d'ammonium à 0,8 mol / L à une température de 85°C. On met en route une
burette automatique qui permet de maintenir le pH à une valeur de 3,8
par ajout d'une solution très concentrée en HCl. On introduit alors 50
mL d'une solution d'urée de concentration 0,2 mol/L préchauffée à une
température où la dissolution de l'urée est quasi nulle, et on
suit au cours du temps l'évolution du volume d'acide ajpouté.
C.2. Montrer que ce protocole permet de considérer que n et h sont constantes.
L'acide HCl ajouté étant très concentré, le volume de la solution est à peu près constant, égal à 1 L.
Le pH est maintenu constant : h = constante.
Le chlorure d'ammonium étant en large excès ( 0,8 x0,95 mol >> 0,2 x0,05 mol) , "n" est constant.
On admet que les valeurs des pKa sont inchangées à la température de l'expérience.
C.3. Exprimer la concentrtion en CO2 dissous ( notée c) en fonction de u, n, h et du temps t.
d[CO2] / dt = k2 k1 u h2 / ( k'1 n + k2 h2 ) = Ku avec K = k2 k1 h2 / ( k'1 n + k2 h2 ) = constante.
d[CO2] = Ku dt
Conservation de l'élément carbone : c +u = u0, avec u0, concentration initiale en urée.
d[CO2] = d c= K(u0-c) dt ; dc / (c-u0) = -K dt.
ln (u0-c) = -Kt + cste.
A t=0, c = 0 : ln u0 = cste ; ln ((u0-c) / u0) = -Kt..
1-c / u0 = exp(-Kt) ; c =u0 (1-exp(-Kt)).
c =u0(1-exp( -k2 k1 h2 / ( k'1 n + k2 h2 ) t).
C.4. Exprimer la concentration en acide ajouté haj
( c'est à dire la concentration qu'aurait l'acide ajouté dans le
réacteur s'il n'avait pas été consommé) en fonction de la concentration
en CO2.
D'après (R2) haj = 2 c.
C.5. Expliquer comment on peut alors déterminer k1 et le rapport k'1 / k2.
haj = [HCl] vajouté / (V+vajouté) ~[HCl] vajouté /V.
haj est proportionnel au volume d'acide ajouté.
ln( 1-haj / (2u0)) = k2 k1 h2 / ( k'1 n + k2 h2 ) t.
ln( 1-haj / (2u0)) = k1 / ( k'1 /k2 ( n / h2) + 1 ) t.
t / ln( 1-haj / (2u0)) =( k'1 /k2 ( n / h2) + 1 ) / k1.
|
|