Injection de
médicaments ou de sang par perfusion et transfusion.
Concours général 2017.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Dans
cette partie, les techniques de la perfusion et de la transfusion sont
étudiées à l’aide des modèles de l’hydrostatique et de l’hydrodynamique
des fluides.
Lors d’une perfusion (ou transfusion), la solution passe du flacon dans
le vaisseau sanguin sous l’effet de la gravité. Le dispositif comprend
généralement une roulette permettant le réglage du débit, un tuyau et
un cathéter (aiguille). Les flacons en verre présentent l’avantage
d’une excellente innocuité chimique mais nécessitent la mise en place
d’une entrée d’air. Il faut que la pression à la sortie du cathéter
soit suffisante pour réaliser la perfusion ou la transfusion, d’où
l’intérêt de suspendre le bocal (ou la poche) à une certaine hauteur.
Il est aussi important que le débit soit bien adapté.
Le système sanguin ou appareil cardiovasculaire est un type de système circulatoire en circuit
fermé qui assure le transport du sang du coeur vers les extrémités et les divers organes, et en
retour de ceux-ci vers le coeur. Le sang est expulsé par le coeur dans l’artère
aorte avec une pression relative moyenne de Prelative = 13 kPa pour un sujet en position horizontale. Cette pression est mesurée par rapport à la pression atmosphérique Patm :
Prelative = Psang – Patm.
Après passage dans la grande circulation (ventricule gauche – aorte – artères – artérioles -
veinules – valvules – veines - veine cave -oreillette droite), le sang revient par la veine cave.
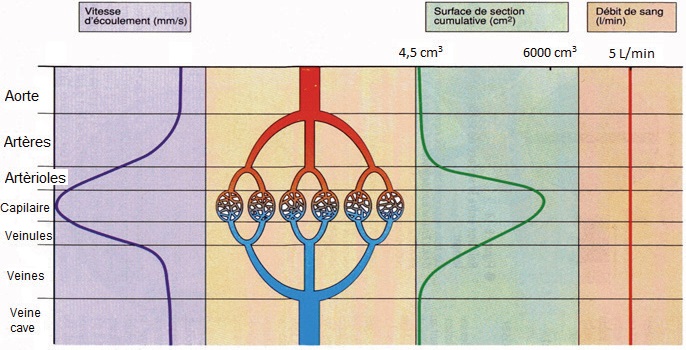
B1. Débit sanguin dans la grande circulation.
24. À partir des documents fournis, donner la valeur du débit volumique sanguin Qv dans la grande
circulation et l’exprimer en mL.s-1.
5 L min-1 ou 5000 / 60 =83,3 mL s-1.
25. Proposer une explication au fait que la section cumulée des capillaires est différente de celle de
l’aorte.
Le débit volumique est constant ; la vitesse du sang dans les capillaires est faible. Or Qv
= v S, avec v vitesse d'écoulement et S section. La conservation du
débit volumique impose une section de l'ensemble des capillaires
supérieure à celle de l'aorte.
Les capillaires étant très nombreux, leur surface cumulée est supérieure à celle de l'aorte.
26. Le débit
volumique sanguin peut être exprimé en fonction de la vitesse v du sang
et de la section S du vaisseau. Identifier la bonne relation parmi les
propositions suivantes et justifier votre réponse.
Relation 1 : Qv = v×S ; Relation 2 : Qv = v / S ; Relation 3 : Qv = S /v.
Débit : m3 s-1 ; vitesse m s-1 ; S : m2. Seule la relation 1 est homogène vis à vis des unités.
27. Un cycle
complet de la grande circulation dure environ 0,85 s et permet au sang
expulsé dans l’aortede revenir par la veine cave.Présenter un
raisonnement argumenté permettant d’interpréter les courbes « surface
de section cumulative » et « vitesse d’écoulement » fournies dans le
schéma de la grande circulation ci-dessus. Calculer les valeurs
maximale et minimale des vitesses d’écoulement.
Qv = v×S = constante. Si v diminue alors S augmente et réciproquement.
Vitesse du sang dans l'aorte : Qv = 5 10-3 / 60 = 8,3 10-5 m3 s-1. S = 4,5 10-6 m3.
v=Qv / S = 8,3 10-5 / 4,5 10-6 =18,4 m s-1.
Vitesse du sang dans les capillaires : Stotale =6 10-3 m3.
v = 8,3 10-5 / 6 10-3 =1,38 10-2 m s-1.
B2. Hauteur de la poche de sang lors d’une transfusion sanguine.
La pression sanguine au niveau de la sortie du coeur est donnée dans le document portant sur
l’appareil circulatoire sanguin 13 kPa. On se place dans un contexte hydrostatique, c’est-à-dire en
considérant le sang au repos.
28. Pour un sujet
allongé, calculer la hauteur à laquelle doit être placée une poche de
sang lors d’une transfusion implantée au niveau de l’artère aorte.
rsang g h >13 103 ; h > 13 103 / (rsang g) ;
h > 13 103 / (1,06 103 x9,81) ; h > 1,24 m.
9. Que se passerait-il si le flacon se trouvait à une hauteur inférieure à la valeur calculée
précédemment ?
Ce n'est pas le liquide de la perfusion qui s'écoulerait dans le sang, mais l'inverse.
|
|
|
B3. Risques encourus lors d’une transfusion sanguine.
L’embolie gazeuse.
Les techniques de voies d’accès au sang par perfusion des grosses veines du cou (veine jugulaire
interne) ou du haut du thorax (veine sous-clavière) ont largement bénéficié des progrès réalisés en
matière de matériaux et de kits prêts à l’emploi. Comme tout acte
médical, ces actes présentent des risques qu’il faut maitriser. Parmi
ces risques, l’embolie gazeuse (ou passage dans le sang d’un gaz,
leplus souvent de l’air), est une complication possible.
Une relation de la dynamique des fluides : l’équation de Bernoulli.
Le théorème de Bernoulli, qui a été établi en 1738 par Daniel Bernoulli, physicien et mathématicien
suisse, est la formulation mathématique du principe de Bernoulli : pour
un fluide en mouvement, une accélération s’accompagne toujours d’une
diminution de la pression du fluide.
Cette relation caractérise aussi la conservation de l’énergie pour un fluide en mouvement.
Pour un écoulement d’un fluide parfait incompressible et en négligeant les transferts thermiques :
½ρ×v2 + ρ×g×h + P = constante
Avec P pression en un point du fluide (en Pa)
ρ masse volumique du fluide (en kg.m-3)
v vitesse du fluide en ce point (en m.s-1)
g accélération de la pesanteur (en N.kg-1 ou m.s-²)
h altitude de ce point du fluide (en m).
Pour simplifier l’étude, on suppose dans un premier temps que le cathéter a le même
diamètre que le tuyau et que la sortie du cathéter est dans l’air. Ce dernier n’est donc
pas implanté dans la veine du patient. L’aérateur permet de maintenir
une pression égale à la pression atmosphérique dans le flacon en
permettant le contact en entre l’air ambiant et l’air dans le flacon.
Q.30. Le sang s’écoule à travers le tuyau. En utilisant l’équation de Bernoulli, établir la
relation P(h) = Patm - ρ×g×h, relation entre la pression P(h) dans le tuyau à une hauteur
quelconque h et la pression atmosphérique Patm.
Le tuyau et le cathéter ayant la même section, la vitesse est constante dans le tyau et le cathéter.
On écrit la relation de Bernoulli entre la sortie du cathéter( h=0) et un point situé à une hauteur h du tuyau.
ρ×g×h + P(h) = Patm ; P(h) = Patm - ρ×g×h.
Q.31. Comment varie la pression le long du tuyau ? Expliquer comment peut survenir une
embolie gazeuse lors d’une transfusion.
P(h) diminue si h augmente. Patm > P(h), l'air peut donc entrer dans le tuyau.
|
|
|
|
32. On appelle h1, la hauteur entre la surface libre du sang et le cathéter.
Écrire l’équation de Bernoulli en considérant les points d’altitude h = 0 et h = h1.
Expliquer pourquoi on peut négliger la vitesse du sang au niveau de la surface libre du sang dans le flacon.
En déduire la relation : Qv = Stuyau× (2g×h1)½.
La surface du flacon est très supérieure à celle du tuyau ; la
conservation du débit conduit à négliger la vitesse du sang au niveau
de la surface libre du sang dans le flacon.
La relation de Bernoulli s'écrit :
ρ×g×h1 + Patm = ½rv2 +Patm ; v2 = 2gh1 ; v = ( 2gh1)½.
Qv = Stuyau× v =Stuyau× (2g×h1)½.
33. D’après la
relation précédente, il est possible d’agir sur deux paramètres pour
accroître le débit volumique du sang au cours de la transfusion. En
argumentant, indiquer le moyen à privilégier pour accroître le débit
tout en limitant le risque d’embolie gazeuse.
Augmenter la surface du tuyau ou la hauteur h1.
On limite le risque d'embolie gazeuse en augmentant la surface du tuyau et en gardant h1 constant.
B4. Prise en compte de la viscosité du fluide transfusé.
Dans un contexte dynamique, en raison des frottements du fluide sur les
parois du tuyau dans lequel il s’écoule, la pression du fluide diminue
au fur et à mesure de sa progression. La loi de Hagen Poiseuille donne
l’expression de cette variation de pression :
ΔP =8×η×L /(π×r4 )×Qv.
ΔP est la variation de pression entre les deux extrémités du tuyau (en Pa), L est la longueur du
tuyau (en m), r son rayon (en m), η la viscosité du fluide (exprimée en Poiseuille Pl ou Pa.s) et
Qv le débit volumique du sang exprimé en m 3.s-1.
La viscosité est une grandeur indiquant le degré de fluidité d'un fluide et donc sa capacité à s’écouler.
Plus la viscosité est importante, plus le fluide est épais et plus il
s’écoule difficilement ; plus la viscosité est faible, plus il s’écoule
facilement. La viscosité s’exprime en Pa.s ou Pl (Poiseuille).
Données : viscosité du sang
ηsang = 1,5 10-3 Pl ; ρsang = 1,06 x 103 kg.m-3 ; g = 9,81 m.s-2.
34. Le sang revient
dans le coeur par la veine cave. La pression relative dans la veine
cave est égale à 1,3 kPa alors que dans l’artère aorte la pression
relative est 13 kPa. Justifier cette baisse de pression.
En raison des frottements du sang sur les parois des veines dans lequel
il s’écoule, la pression dusang diminue au fur et à mesure de sa
progression.
35. On considère un
cathéter de longueur L = 5,0 cm de diamètre intérieur d = 1,0 mm,
calculer la différence de pression entre l’entrée et la sortie de ce
cathéter pour un débit volumique de transfusion de valeur Qv = 1,0 mL.s-1.
ΔP =8×η×L /(π×r4 )×Qv = 8 x1,5 10-3 x0,05 x1,0 10-6 / (3,14 x(5 10-4)4) =3,06 103 Pa.
36. On s’intéresse
à une transfusion dans la veine cave. En négligeant la variation de
pression dans le tuyau, déterminer la valeur de la hauteur minimale à
laquelle doit être accrochée la poche de sang pour que la transfusion
soit effectuée dans de bonnes conditions.
rsang g h >1,3 103 ; h > 1,3 103 / (rsang g) ;
h > (1,3 103 + 3,06 103) / (1,06 103 x9,81) ; h > 0,42 m.
La loi de Haguen Poiseuille peut se mettre sous la forme ΔP = R x Qv, R étant la résistance à l’écoulement.
37. Comparer
qualitativement la résistance à l’écoulement à travers le cathéter à
celle à travers le tuyau. Argumenter soigneusement votre réponse.
La section du tuyau est bien supérieure à celle du cathéter ; de plus la perte de charge DP
est inversement proportionnelle au rayon à la puissance 4. La
résistance à l'écoulement à travers le tuyau est très inférieure à
celle à travers le cathéter.
38. Justifier l’approximation faite à la question 36.
A une faible résistance à l'écoulement correspond une faible perte de charge DP.
|
|
|
|