Coulomb et les
lois du frottement solide
Concours général 2017.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
1.A Coulomb et le frottement statique.
Nous avons fait construire une table très solide sur laquelle on a posé
deux poutres de bois de chêne AB et A'B'. A l'extrémité BB' des pièces
de bpois, l'on a placé, dans le vide qui les sépare, une poulie en bois
: sous cette poulie l'on a creusé un puits pour pouvoir y laisser
descendre le plateau P.
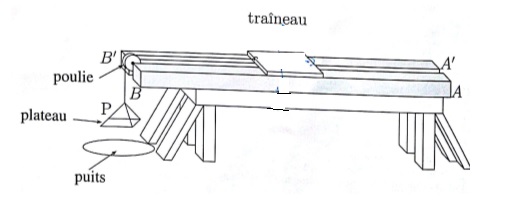
L'on a fait successivement glisser sur les pièces de bois de chêne un
traineau. Lorsqu'on veut diminuer les surfaces en contact, on cloue
sous le traineau des règles de différentes largeurs. Un crochet fixé à
une extrémité du traîneau sert à attacher une corde qui passe par la
poulie, et porte le plateau P.
Extrait adapté des pages 5 à 7 de la théorie des machines simples.
Il est usuel de décomposer la force exercée par le support ( ici, les
poutres) sur le traîneau à l'aide de deux composantes : l'une
tangentielle ( parallèle ) au support et notée T, l'autre normale au
plan du support et notée N.
Le système étudié est le traîneau.
1. Représenter les forces auquelles le traîneau est soumis.
Le traîneau est soumis à son poids P, à l'action du support et à l'action de la corde notée F.

2. Justifier
l'orientation ( direction et sens) du vecteur N. relier N, la masse m
du traîneau éventuellement chargé et g l'intensité de la pesanteur.
A l'équilibre le vecteur N est opposé au vecteur poids du traîneau. ce
vecteur N est vertical, dirigé vers le haut, de norme N = mg.
3.4.5. Justifier l'orientation du vecteur T.
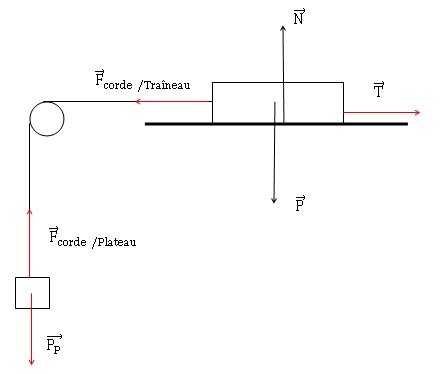
Les frottements s'opposent au déplacement.
A l'équilibre les vecteurs Fcorde/traîneau et T sont opposés. Le vecteur T est horizontal, dirigé vers la droite, de norme T = mP g avec mP masse du plateau et de son chargement..
6. Calculer le rapport T / N pour les expériences suivantes.
l'on veut déterminer le frottement après un certain temps de repos, sous différents poids.
Expérience 1. le traîneau pesant 74 livres, n'est pas chargé ; il a fallu une traction de 30 livres pour vaincre le frottement.
T / N = 30 / 74 ~0,41.
Expérience 2.
le traîneau chargé, son propre poids compris, pèse 874 livres ; il a
fallu une traction de 406 livres pour vaincre le frottement.
T / N = 406 / 874 ~0,46.
Expérience 3.
le traîneau chargé, son propre poids compris, pèse 2674 livres ; il a
fallu une traction de 1116 livres pour vaincre le frottement.
T / N = 1116 / 2674 ~0,42.
Une des lois du frottement solide, énoncée par Coulomb, stipule qu'il existe un coefficient statique µs indépendant de m, tel que T < µs N tant qu'il n'y a pas glissement.
7. Expliquer comment les expériences précédentes on conduit Coulomb à formuler cette loi.
Les trois expériences indiquent que le rapport T / N , à la limite du glissement, est à peu près constant, indépendant de la masse du chariot chargé ou non.
A la limite du glissement T = µs N.
Tant qu'il n'y a pas glissement, T < µs N.
8. Estimer la valeur du coefficient µs pour le frottement chêne / chêne étudié.
µs = (0,41 +0,42 +0,46 ) / 3 ~0,43.
Sous le
traineau de 15 pouces de longueur, j'ai fait clouer deux petits prismes
triangulaires de bois de chêne de 15 pouces de longueur, mais dont
l'angle qui portait sur les poutres AB et A'B' était arrondi.
4è expérience
: le traîneau chargé, son poids compris, a une masse de 250 livres.
l'on trouve que la traction nécessaire pour vaincre le frottement est
de 106 livres.
5è expérience
: le traîneau chargé, son poids compris, a une masse de 450 livres.
l'on trouve que la traction nécessaire pour vaincre le frottement est
de 186 livres.
6è expérience
: le traîneau chargé, son poids compris, a une masse de 856 livres.
l'on trouve que la traction nécessaire pour vaincre le frottement est
de 356 livres.
Extrait adapté de la page 10 de la théorie des machines simples.
9.
En s'appuyant sur des évaluations quantitatives et éventuellement un
schéma, expliquer ce qu'apportent les expériences 4 à 6 par rapport aux
expériences 1 à 3.
Expérience 4 :T / N = 106 / 250 ~0,42 ; expérience 5 : T / N = 186 / 450 ~ 0,41 ;
expérience 6 : T / N = 356 / 856 ~042.
Le coefficient µs ne dépend pas de l'aire de la surface de contact, mais de la nature des matériaux, de leur rugosité et de la lubrification.
|
|
|
I.B Coulomb et le frottement dynamique.
Dans
les expériences suivantes, les mesures sont effectuées sur une distance
parcourue par le traîneau de 4 pieds ( environ 1,20 m ). On étudie une
phase de glissement. Coulomb fait relever la durée Dt1 de parcours des 2 premiers pieds, puis celle notée Dt2 des deux derniers.
La durée des mouvements s'observait au moyen d'un pendule qui battait les demi-secondes.
Expérience
|
Masse du traîneau
chargé ( livres)
|
Masse du plateau
chargé ( livres)
|
Dt1 (s) |
Dt2 (s) |
Dt2 /Dt1 |
Surface de contact
(pouces carré)
|
1
|
47
|
9
|
1,5
|
0,5
|
0,33
|
36
|
2
|
1647
|
162
|
14
|
6
|
0,43
|
36
|
3
|
1647
|
166
|
5,5
|
2,5
|
0,45
|
36
|
4
|
1647
|
172
|
4,5
|
2
|
0,44
|
36
|
5
|
874
|
105
|
3
|
1,5
|
0,5
|
432
|
6
|
2474
|
270
|
4
|
2,5
|
0,62
|
432
|
10. Discuter de la qualité des résultats expérimentaux.
Les durées inférieures à 2,5 s sont très imprécises, le pendule battant la demi-seconde.
L'incertitude relative sur la durée dépasse 20 %.
On note d la distance qui
sépare deux points éloignés de 2 pieds et a l'accélération du traîneau
lors du mouvement. Coulomb fait l'hypothèse que le mouvement du
traîneau est uniformément accéléré.
11. Exprimer Dt1 en fonction de d et a.
Pour les deux premiers pieds : d =½a Dt12.
Pour les deux pieds suivants : 2d = ½a ( Dt1+Dt2 )2.
12. En déduire que Dt2 = a Dt1 où a est un nombre à déterminer.
2(½a Dt12)=½a ( Dt1+Dt2 )2 ; 2 Dt12=( Dt1+Dt2 )2 ; 1,414 Dt1= Dt1+Dt2 ; Dt2 =0,414 Dt1.
13.
Cette valeur est-elle en accord avec les résultats de Coulomb ? En
déduire qu'aux incertitudes de mesures près, le mouvement est
effectivement accéléré.
Pour l'expérience 1, l'incertitude sur Dt2 est trop grande.
La principale incertitude concerne la mesure du temps, le pendule battant la demi-seconde.
La valeur trouvée est
en bon accord avec les expériences 2, 3 et 4, l'hypothèse d'un
mouvement uniformément accéléré est confirmée.
14.
Comment améliorer le dispositif de Coulomb, en utilisant du matériel
moderne, pour pouvoir trancher sur le caractère uniformément accéléré
du mouvement ?
Utiliser un banc à coussin d'air, les capteurs, fourches optiques,
étant reliés à une interface, reliée elle-même à un ordinateur.
15 Montrer que la norme de l'accélération du plateau est égale à celle du traîneau au cours du mouvement.
Hypothèses : fil inextensible de masse négligeable devant les masse du traîneau et du plateau chargé.
Masse de la poulie négligeable devant celles du traîneau et du plateau chargé.
Avec ces hypothèses, le traîneau et le plateau ont la même accélération.
|
|
|
|
il est usuel d'introduire un second coefficient de frottement, noté µd et appelé coefficient de frottement dynamique, qui relie N et T lorsqu'il y a glissement, et tel que T = µd N.
16. La valeur de a dépend-elle des coefficients de frottement ?
Non, a, rapport de deux durées, est indépendant de l'accélération.
17. Exprimer µd en fonction de Dt1, d, g, m et mP.
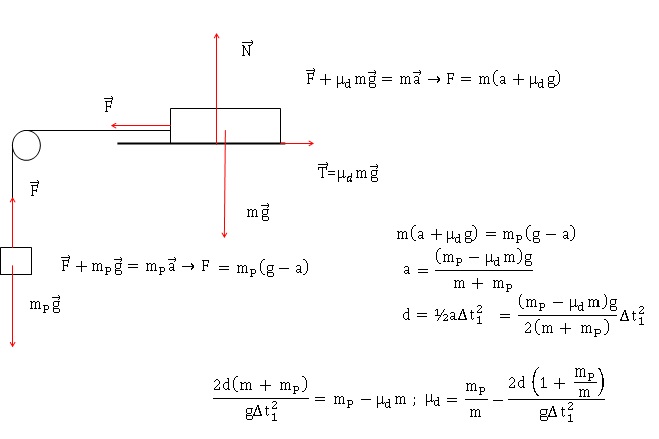
18. Calculer la
valeur du coefficient µd pour chaque ligne du tableau. Commenter les résultats obtenus. En déduire une estimation du coefficient µd pour le frottement chêne /chêne. d ~0,30 m.
Expérience
|
m ( livres)
|
mP ( livres)
|
mP / m
|
Dt1 (s) |
µd |
Surface de contact
(pouces carré)
|
1
|
47
|
9
|
0,1915
|
1,5
|
0,159
|
36
|
2
|
1647
|
162
|
0,09836
|
14
|
0,098
|
36
|
3
|
1647
|
166
|
0,1008
|
5,5
|
0,0986
|
36
|
4
|
1647
|
172
|
0,1044
|
4,5
|
0,101
|
36
|
5
|
874
|
105
|
0,1201
|
3
|
0,112
|
432
|
6
|
2474
|
270
|
0,1091
|
4
|
0,105
|
432
|
µd ~0,11.
19. Comparer µd et µs. Commenter qualitativement ce résultat
µd < µs.
La force nécessaire pour entretenir le glissement est inférieure à la force limite d'adhérence.
20. La valeur de µd dépend-elle de l'aire des surface en contact ?.
Non, elle dépend de la nature et de la rugosité des surface en contact.
Initialement, Coulomb avait envisagé de laisser le traîneau
avancer sur 12 pieds ( au lieu de 4), mais il s'est rapidement
rendu compte qu'au bout d'une telle distance parcourue, l'expérience
devenait dangereuse.
21. Estimer la
vitesse atteinte par le traîneau chargé, de masse totale environ 800
kg, au bout de 3,0 m de course ( avec une vitesse initiale négligeable
et un plateau chargé d'environ 90 kg ). Commenter le résultat.
a = 9,81(90-0,11 x800) / 890=0,022 m s-2.
v2 = 2 a d =2 x0,022 x3 = 0,132 ; v =0,36 m s-1.
Energie cinétique finale du traîneau : 0,5 x800 x0,132 ~53 J.
( le danger n'est pas lié à l'énergie cinétique, mais à la chute éventuelle du traîneau massif arrivé en bout de table ).
I. C. Version moderne de l'expérience de Coulomb.
A l'aide d'un banc d'essai, on peut estimer les
coefficients de frottement pour le contact papier / papier entre deux
feuilles de papier.
L'appareil est composé d'une table qui se déplace par rapport au sol, le long d'un axe, et d'un traîneau ( de masse 1,0 102
g) qui est maintenu fixe par rapport au sol, par une plaque munie d'un
capteur de force. Une pince maintient une première bande de papier sur
une surface adhérente en caoutchouc, solidaire de la table. Une seconde
bande de papier est fixée sur la face inférieure du traîneau au moyen
d'un dispositif de serrage. Au début d'une mesure, le traîneau est
abandonné sans vitesse sur la table d'essai. On pousse alors lentement
la table. Le capteur de force enregistre la courbe suivante en fonction
du temps.
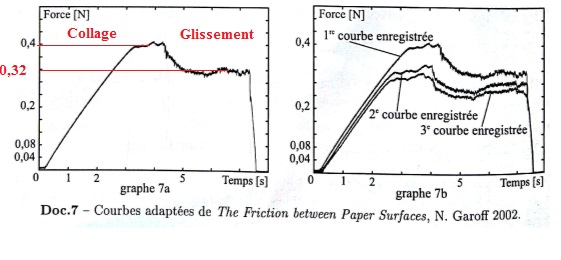
On s'intéresse d'abord au graphe 7a. Durant la phase de glissement, la table a une vitesse d'environ 20 mm s-1, alors que dans la phase de collage sa vitesse est d'environ 60 µm s-1.
22. Le capteur de force qui équipe le banc permet-il de mesurer T ou N ?
Le capteur de force mesure T.
23. Situer sur le graphe a les phases de glissement et de collage.
24. A partir du graphe, estimer les valeurs des coefficients de frottement statique et dynamique.
N ~0,1 *9,8 ~1 N ; µs = T / N =0,4 / 1 = 0,4 ; µd =0,32.
25. Retrouve t-on la même inégalité entre les coefficients µs et µd pour le contact papier / papier que pour le contact chêne / chêne ?.
Oui, µd < µs.
26. Estimer la taille minimale à prévoir pour le banc d'essai pour réaliser cette expérience.
Durée de la phase de collage : 4 s ; vitesse 60 µm s-1. Disatnce parcourue : 60 x4 = 240 µm ou 0,24 mm.
Glissement : durée : 5 s ; vitesse 20 mm s-1, distance parcourue : 20 x5 = 100 mm ; total ~10 cm.
Pour plusieurs expériences successives, la longueur du banc est de quelques dizaines de centimètres.
Le graphe 7b représente trois courbe enregistrées successivement (
toujours pour un même sens de déplacement de la table): d'abord le
première, puis la seconde, puis la troisième.
27. Quelle propriété remarquable ce graphe fait-il ressortir ? Comment expliquer ce phénomène ?
Les coefficients de frottement diminuent d'environ 10 % entre la
première expérience et la seconde, beaucoup moins entre la seconde et
la trosième. Lors de la première expérience, il y a eu usure des
surfaces de papier.
On fournit habituellement un intervalle de valeurs pour chaque coefficient de frottement.
28. Le graphe 7b permet-il de comprendre ce choix ? Proposer un intervalle de valeurs pour les coefficients de frottements étudiés.
µs est compris entre 0,3 et 0,4 ; µd est compris entre 0,24 et 0,3.
Coulomb n'indique pas s'il a pris soin de vérifier l'horizontalité des faces supérieures des pièces de bois AB et A'B'.
29. Une parfaite
horizontalité est-elle essentielle au vu des résultats de cette étude ?
On attend des élément de raisonnement quantitatif.
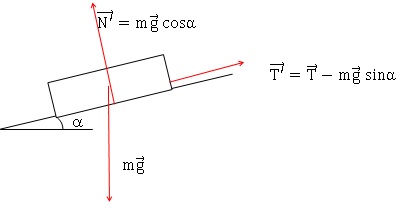
Pour a de l'ordre de 5 °, cos 5 ~0,996 : N' ~N.
sin 5 ~0,087 : T' ~ T.
Une parfaite horizontalité n'est pas essentielle au regard de la précision sur la mesure des durées.
I.D. Quelle meilleure stratégie pour faire glisser une caisse ?
Un déménageur cherche à déplacer une caisse en bois remplie, posée sur un parquet. Il veut la faire glisser en la tirant.
30. Comment doit-on
tirer la caisse pour exercer la force la plus faible possible :
horizontalement, verticalement, à l'oblique. Dans ce dernier cad, on
précisera l'angle. Ce résultat dépend-il de la nature du revêtement au
sol ?
Pousser la caisse demande moins d'effort que pour la tirer puisqu'on utilise son propre poids pour aider au déplacement.
Pour faciliter le glissement, placer des patins en téflon autocollants
sous la caisse, le coefficient de frottement statique sera plus faible..
Quand il n'est pas possible de pousser ou de placer les patins :
- Exercer une force verticale vers le haut, ne fera pas glisser la caisse.
- Exercer une force horizontale : F > µbois / bois mg.
Pour une caisse de masse m = 20 kg ; µbois / bois mg = 0,4 x10 x20 = 80 N. F > 80 N.
- Exercer une force oblique F.
La force nécessaire pour entretenir le glissement est inférieure à la force limite d'adhérence.
On se place à la limite du cône d'adhérence.
Exercer une force oblique vers le haut, dont la direction fait un angle a avec la verticale, égal à l'angle limite du cône d'adhérence.
Dans le cas chêne / chêne : µs ~0,4 ; tan a ~0,4 et a ~22°.
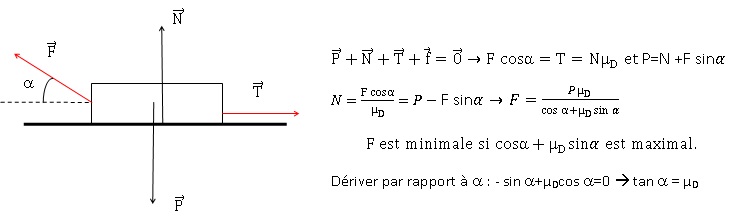
Pour a = 22° et m = 20 kg, on trouve F ~74 N, valeur inférieure à 80 N.
|
|
|
|