Ester,
échographie, thermique, mécanique.
Concours Geipi Polytech 2017.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Exercice
1.
Le formiate d’éthyle (noté E) est un composé chimique à l’odeur de
framboise.
On étudie la saponification du formiate d’éthyle par la soude :
HCOOCH 2CH 3 + HO - → HCOO - +
CH 3CH 2OH
Masse volumique du formiate d’éthyle : rE = 918 g.L -1.
Conductivités ioniques molaires des ions en S.m2.mol-1 :
l(Na +)
= 5,0.10 -3 ; l(HO-) = 19,9.10-3 ; l(HCOO-) = 5,5.10-3 .
I-1- Donner le nom
de E en nomenclature systématique.
Méthanoate d'éthyle.
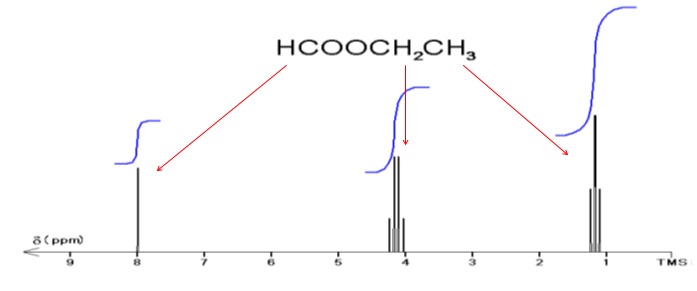
I-2- Entourer les
différents groupes de protons de la molécule E puis relier par une
flèche
chacun des groupes au signal qui lui correspond sur le spectre RMN 1H.
On prépare V s =200mL de solution aqueuse S de soude de
concentration c Soude = 5,0.10 -2 mol.L -1.
I-3- Donner
l’expression puis calculer la masse de soude qu’il a fallu dissoudre
dans l’eau pure
pour obtenir la concentration souhaitée.
n soude = V s c soude ; m = Vs csoude
m(NaOH) = 0,200 x5,0 10-2 x40 =0,40 g.
I-4- Calculer le pH
de la solution de soude.
pH = 14 + log (5 10 -2) = 12,7.
La solution de soude est introduite dans un réacteur muni d’une sonde
conductimétrique reliée à
un conductimètre ainsi que d’un système d’agitation mécanique.
On rappelle que la conductivité G d’une
solution ionique s’écrit G = k x
S li
C i.
I-5- Connaissant la
constante de cellule k = 0,01 m, déterminer l’unité de G dans le système
d’unité international (S.I.). Calculer alors la valeur théorique de la
conductivité G 0 à t = 0.
G s'exprime en : m S.m2.mol-1
mol m-3 soit S.
La concentration des ions s'exprime en mol /m3 soit 5,0 10-2
x1000 = 50 mol m-3.
G = k (l(Na+) + l(HO-) = 0,01 x (5,0.10-3 +
19,9.10-3 ) x 50=0,0125 S.
On introduit à t = 0, n Eo = 5,0 mmol de l’ester E.
I-6- Donner
l’expression puis calculer le volume V E de E qu’il faut
introduire.
nEo M(E) / rE =5,0 10-3 x 74 / 918 =
4,0 10-4 L = 0,40 mL.
Ce volume sera négligé devant V s et on considérera le volume
total V = 200 mL dans toute la suite
du problème.
I-7- Choisir parmi
les 6 graphiques du document réponse la forme de courbe qui donne
l’évolution de la conductance mesurée G en fonction du temps.
Du point de vue de la conductivité, tout ce passe comme si on
remplaçait l'ion HO - par l'ion formiate, de conductivité
molaire ionique moindre. La conductance diminue donc puis est constante
en fin d'hydrolyse basique.
 I-8
I-8- Dans les
conditions dans laquelle elle est menée, la réaction peut être
considérée comme totale. Compléter le tableau d’avancement.
|
HCOOCH2CH3
|
+
HO- |
→
HCOO- |
+
CH3CH2OH |
tinitial
|
5,0
|
200 x0,05=10
|
0
|
0
|
tfinal
|
0
|
5,0
|
5,0
|
5,0
|
On déduit de la mesure de G la variation de la variable d’avancement x
en fonction du temps.
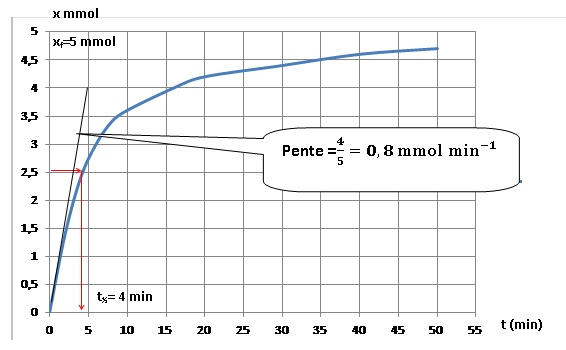
I-9- A partir de la
courbe x = f(t) ci-après, déterminer la vitesse initiale v 0
de la réaction et le temps t ½ de demi réaction.
La vitesse initiale est égale à la pente de la tangente à l'origine.
A t ½, l'avancement est égal à la moitié de l'avancement
final soit 2,5 mmol.
|
|
|
Exercice 2.
L’échographie est une technique médicale permettant de détecter la
présence de calculs rénaux en utilisant une sonde à ultrasons. Les
sondes ultrasonores sont des céramiques piézoélectriques fonctionnant
successivement en émission et en réception.
Propagation d’une onde ultrasonore dans l’air.
II-1- Quelle est la
grandeur physique qui varie dans une onde ultrasonore ?
La pression.
II-2- Donner les
caractéristiques d’une onde ultrasonore.
Onde mécanique progressive longitudinale transportant de l'énergie.
II-3- Quelle est la
fréquence minimale des ultrasons ?
20 kHz.
Propagation d’une onde ultrasonore dans les tissus.
La vitesse de propagation des ultrasons est :
dans le tissu vtissu = 1400 m.s-1, dans le rein vrein
= 1500 m.s-1, dans le calcul rénal vcalcul =
1540 m.s-1.
On suppose que dans le tissu, le rein ou le calcul, la vitesse de
l’onde ultrasonore est indépendante de la fréquence.
II-4-
Comment qualifie-t-on ces milieux ?
Ces milieux sont non dispersifs.
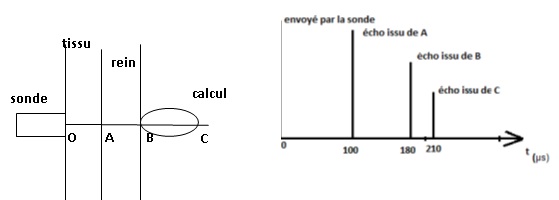
Une onde
ultrasonore incidente est émise à l'instant t=0 au point O. On donne
l’enregistrement des échos
renvoyés par les surfaces de séparation des différents milieux : sur le
rein en A, sur le calcul
rénal en B puis en C.
II-5- A quelle distance OA de la surface de la
peau est située la surface du rein ?
1400 x100 10-6 /2= 0,07 m = 7 cm.
II-6- La résolution
spatiale est de l’ordre de grandeur de la longueur d’onde. Donner
l’expression
puis calculer la longueur d'onde l1 des ultrasons
dans le rein pour une fréquence de f1 = 3.5 MHz puis l2 pour f2 =10 MHz.
l1
= 1500 / (3,5 106)=4,3 10-4 m ; l2
= 1500 / (10 106)=1,5 10-4 m .
II-7- Calculer la longueur BC du
calcul rénal.
1540 x(210-180)10-6 / 2 = 0,023 m = 2,3 cm.
Les ondes émises par la sonde ont un niveau d'intensité ultrasonore L1
= 100 dB.
II-8- Que vaut
l’intensité I1 correspondante en W.m-2 ?
I1 = I0 100,1 L = 10-12 x 1010
= 10-2 W
m-2.
L'atténuation de l'intensité suit la loi Itransmise =I exp(-ax)
avec x, l’épaisseur du milieu et a son coefficient d’atténuation qui croît avec
la fréquence des ultrasons. L’atténuation est
approximativement de
1dB/cm/MHz.
II-9- Justifier pourquoi pour
étudier un rein situé à plus de 5 cm de la peau, on utilise un émetteur
ultrason à 3.5 MHz
plutôt qu’à 10 MHz ?
L'atténuation à 3,5 MHz est égale à 5x2 x3,5 = 35 dB ; l'atténuation à 10 MHz est égale à 5 x2
x10 = 100 dB ;
l'onde réfléchie ne peut pas être détectée.
II-10-
Justifier pourquoi pour étudier une thyroïde située à moins de 2 cm de
la peau, on utilise un
émetteur ultrason à 10 MHz plutôt qu’à 3.5 MHz ?
L'atténuation
à 3,5 MHz est égale à 2x2 x3,5 = 14 dB et la résolution
spatiale est de 4,3 10-4 m = 0,43 mm ; l'atténuation à 10 MHz est égale à 2 x2
x10 = 40 dB mais la
résolution spatiale est meilleure de l"ordre de 1,5 10-4
m = 0,15 mm.
|
|
|
|
Exercice 3.
Charles a l’habitude de prendre son café bien chaud. Il utilise un
gobelet en verre contenant un volume V = 300 mL de café, initialement à
une température de T1= 66 °C. Il laisse son gobelet dans son
salon qui est à une température de T2=18 °C.
Progressivement, la température du café
diminue pour finalement se stabiliser à la température de la pièce. Au
cours de cette transformation thermodynamique, l’énergie interne du
café varie. On considère la masse volumique du café rc= 1,00 kg/L et
la capacité calorifique massique du café cc=4 200 S.I.
III-1- De manière
générale, quel est l’origine microscopique de la variation d’énergie
interne ?
L'énergie interne est égale à la somme des énergies cinétique et
potentielle microscopiques.
III-2- Rappeler
l’expression du premier principe de la thermodynamique dans le cas d’un
tel système.
DU =
W+Q.
III-3- Durant cette
transformation, le travail est reçu par le café, perdu par le café ou
nul ?
Le gobelet ne se déforme pas, le travail est donc nul.
III-4- Dans le cas
de cette transformation, la quantité de chaleur est reçue par le café,
perdue par le café ou nulle ?
Le café chaud cède de l'énergie au milieu extérieur. La quantité
de chaleur est perdu par le café.
III-5- Donner
l’expression de la variation d’énergie interne du café ΔU en fonction
des températures T1 et T2.
DU = rc Vc cc(T2-T1).
III-6- Quelle est
l’unité de la capacité calorifique massique ?
J kg-1 K-1.
III-7- Calculer la
variation d’énergie interne ΔU.
DU =103
x 300 10-6 x 4200 (66-18)= -60480 ~ -6,0 104 J.
Charles se rend compte que le café est trop froid, et n’est plus à son
goût. Il décide de le réchauffer cette fois-ci en utilisant son four à
micro-ondes. Pour cela, il le règle sur la position 3 et durant 30
secondes. Le café atteint une température T3=39,5 °C.
III-8- Quel est le
type de transfert thermique réalisé entre le four et le café ?
Transfert par énergie rayonnante.
On rappelle que la relation entre la quantité de chaleur Q et la
puissance thermique P lorsque celle-ci est constante s’écrit : |Q| = P
. Δt
III-9- Donner
l’expression puis calculer la quantité de chaleur échangée entre le
four et le café.
DU =103
x 300 10-6 x 4200 (39,5-18)= +27090 ~ +2,7 104 J.
III-10- Durant
cette transformation, la quantité de chaleur est reçue par le café, perdue par le
café ou nulle ?
III-11- À quelle
puissance thermique correspond la position 3 du four ?
P = Q / Dt =27090
/ 30 = 903 W.
Lorsque Charles s’empare du gobelet en verre avec sa main, il est
brûlant. Par manque d’attention, Charles a réglé la minuterie à 1
minute, de sorte que la température du café dans le gobelet est
finalement de 60 °C (T4)
On rappelle que : Rth = e /(lS) et F = DT / Rth.
III-12- Quelle est
la nature du transfert thermique à travers la paroi du gobelet en verre
?
Transfert thermique par conduction.
La paroi du gobelet a une épaisseur de e1=1,5 mm. La surface
S du gobelet est égale à 250 cm2.
On mesure le flux thermique à travers la paroi de verre Φv= 70 W.
On donne la conductivité du verre : λv=1,0 W.m-1·K-1.
III-13- Que vaut la
résistance thermique Rv du gobelet ?
Rv = 1,5 10-3 /(1,0 x250 10-4)=0,06 K W-1.
III-14-
Que vaut la différence de température |ΔT| entre la paroi intérieure et
la paroi extérieure du gobelet ?
|ΔT| =0,06 x70 = 4,2°C.
Charles décide de changer de gobelet et d’en utiliser un de la même
forme mais d’une épaisseur e2 plus grande. La température de
la paroi du gobelet atteint finalement T5=35 °C. On admet
que le flux thermique reste inchangé (Φv= 70 W).
III-15- Donner
l’expression littérale de l’épaisseur e2 du gobelet en verre
en fonction de la conductivité λv, la surface S, le flux thermique Φv
et la différence de température |ΔT| entre la paroi extérieure et la
paroi intérieure du gobelet. Calculer l’épaisseur e2 du
gobelet en verre ?
Rv = e2 /(λvS) ; Φv
= DT / Rv = DT λvS /e2 ; e2
= DT λvS / Φv .
DT =
60-35 =25°C.
e2 =25 x 1,0 x 250 10-4 / 70 =8,9 10-3
m=8,9 mm.
|
Exercice 4.
Lors de son record du monde (Berlin 2009) Usain Bolt (h = 194 cm, m =
86 kg) en 41 foulées a couru la distance de 100 m en 9,58s. Pour
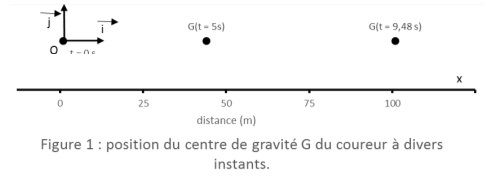
étudier cette course, le coureur est réduit à
une masse ponctuelle située en son centre de gravité, se déplaçant à
hauteur constante dans la direction (Ox) : l’origine O du référentiel
est le centre de gravité du coureur au départ, l’axe (Ox) est dirigé
dans la direction de la piste et dans le sens de la course. l'axe (Oz)
est vertical et dirigé vers le haut.
xG(t) est la position du centre de gravité dans la direction
(Ox) à l’instant t, T est le temps officiel du chronométrage, t est la durée de réaction
(0,14s) l’intervalle de temps entre le
déclenchement du chronomètre et la mise en mouvement du coureur, le
temps t = T- t est
le temps depuis la mise en mouvement, c’est le temps utilisé dans les
modèles suivants.
IV-1- Calculer la valeur moyenne de la vitesse du coureur sur cette course en m.s-1, en km.h-1 et en foulées.min-1.
100 / 9,58 = 10,4 m s-1 ou 10,2 x3,6 = 37,6 km h-1 ; 41 / 9,58 x60 =257 foullées min-1.
La poussée horizontale Fp est la force initiale exercée par le coureur sur les starting-blocks. La poussée de Usain Bolt vaut FO= 685 N.
IV-2- Représenter
sur le document réponse la poussée et la force qui propulse le coureur.
Quel est le nom du principe ou de la loi à l’origine de la force de
propulsion ?
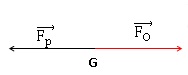 3è loi de Newton. 3è loi de Newton.
On considère que le coureur soit capable de maintenir durant toute la course une force résultante horizontale FO= 685 N.
IV-3- Donner l’expression de l’accélération a du coureur en fonction de Calculer a.
a = FO / m = 685 /86 =7,97 m s-2.
IV-4- Quel est le type de ce mouvement ?
Ce mouvement est rectiligne uniformément accéléré.
IV-5- Quelle est la relation entre l’accélération a(t) et la vitesse v(t) ?
v(t) = a t + Constante ou a = dv /dt.
Quelle est la relation entre la vitesse v(t) et la position instantanée xG(t) ?
v(t) = dxG /dt.
IV-6- Démontrer que la position du centre de gravité du coureur s’écrit xG =3,98 t2.
v = 7,97 t, la vitesse initiale étant nulle.
xG = 7,97 / 2 t2 = 3,98 t2, la position initiale étant l'origine du repère.
IV-7- D’après ce modèle, en combien de temps le coureur parcourt-il les 100 m de la course ?
t = (100 /3,98)½ =5,0 s.
IV-8- Quelle serait la vitesse du coureur à la fin de la course ?
v =7,97 x5 =39,9 m /s.
Le modèle précédent donne des résultats incohérents. Il peut être
amélioré si l’on considère que le coureur rencontre une résistance
proportionnelle à sa vitesse de déplacement. Les forces
responsables du mouvement s’écrivent alors : 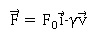
L’équation différentielle du mouvement s’écrit alors ma(t) = FO-g v(t) . La solution de cette équation est v(t) = FO / g(1-exp(-gt / m)).
avec g =55,7 kg s-1 et FO = 685 N
IV-9- Calculer la vitesse v final puis la force Ffinal et enfin l’accélération a final en fin de course pour t = 9,44 s. Que peut-on dire du mouvement en fin de course ? Justifier.
vfinal = 685 / 55,7 (1-exp(-55,7 x9,44 / 86))=12,271 ~ 12,3 m s-1.
vfinal est constante le terme en exponentielle est proche de zéro. Le mouvement est rectiligne uniforme.
Ffinal = FO-g v(t) =685-55,7 x12,271 = 1,5 N.
afinal =Ffinal / m = 1,5 / 86 = 0,018 m s-2.
IV-10- Calculer le travail W de la force FO sur les 100 mètres de la course. Calculer l’énergie cinétique Ec finale du coureur. Calculer en pourcentage, le rendement énergétique du coureur.
W = 100 x 685 =6,85 104 J. Ec finale = ½mv2finale =0,5 x86 x12,2712= 6,475 103 J.
Ec finale / W = 6,475 / 68,5 = 0,094 ( 9,4 %).
.
|
|