Mathémmatiques,
Concours EMIA 2017.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
|
Exercice 1. Exprimer à l'aide de ln 2 et ln 3 :
A = ln 96 =ln (3 x 2 5) = ln3 + 5 ln2.
B = ln(6 5) = 5 ln6 = 5(ln2+ln3).
C= 1 / ln12 = 1/ ln12 =1 / ln(2 2x3) = 1 / (2ln2+ln3).
D = ln (1/12) = -ln12 = -(2ln2 +ln3).
E = ln(18 x36) = ln (3 4 x2 3)= 4 ln3 +3 ln2.
F = ln (12+36) = ln 48 = ln(2 4 x3) = 4 ln2 + ln3.
Exercice 2.
Simplifier les expressions suivantes.
 Exercice 3.
Exercice 3.
Résoudre dans R les inéquations suivantes : e x-1 >1 ; x-1 > ln1 ; x-1 >0 ; x >1. ln(2-x) > 0 ; 2-x > e 0 ; 2-x > 1 ; x < 1.
De plus 2-x > 0 ; x < 2.
|
|
|
|
Exercice 4.
Soit E et F deux points du plan d'affixe respective zE et zF. Que représente |zE-zF| ?
|zE-zF| représente la distance EF.
{M(z) /P} désigne l'ensemble des points M d'affixe z vérifiant la
propriété P. Interpréter géométriquement les ensembles de points du
plan suivants :
A = {M(z) / |z+i+1 | < 2}
z= x +iy ; z+i+1 = x+1 +i(y+1).
|z+i+1|2 = (x+1)2 +(y+1)2 < 4.
Il s'agit de l'ensemble des points contenu à l'intérieur d'un
cercle ( circonférence comprise ) de rayon R = 2 et centré au
point de coordonnées (-1 ; -1).
B = {M(z) / |z-1+2i| =|z+2-i|}.
|z-1+2i| 2= (x-1)2 +(y+2)2 ; |z+2-i| 2= (x+2)2 +(y-1)2 ;
(x-1)2 +(y+2)2 = (x+2)2 +(y-1)2 ;
(x-1)2- (x+2)2 =(y-1)2 -(y+2)2 ; -3 -6x= -3 -6y soit la droite d'équation y = x.
C = {M(x) / |z-i| = -1}.
|x+i(y-1|)| = -1.
|z-i| doit être positif. Donc ensemble vide.
Exercice 5.
1. Soit fla fonction définie sur ]-1 ; +oo[ par f(t) = ln(1+t) -2t /(1+t).
Etudiier le sens de varaiation e f sur [1 ; +oo( et justifier qu'il existe un seul réel a >1 tel que f(a) =0.
Dérivée de ln(1+t) : 1 / (1+t).
Dérivée de -2t /(1+t) en posant u = -2t et v = 1+t ; u' = -2 ; v' = 1.
(u'v-v'u/ / v2 = (-2(t+1) +2t) /(1+t)2= -2 /(1+t)2.
f '(t) = 1/(1+t) - 2 /(1+t)2 = (1+t-2) / (1+t)2 = (t-1) / (1+t)2.
f '(t) est positive sur [1 ; +oo[ ; f(t) est strictement croissante sur cet intervalle.
f '(t) est négative sur ]-1 ; 1 [ ; f(t) est strictement décroissante sur cet intervalle.
f '(x) = 0 pour x = 1 ; f(t) présente un minimum pour x = 1.
f(1) = ln2- 1 <0 ;d'après le corrolaire du théorème des valeurs intermédiaires, il existe un seul réel a >1 tel que f(a) =0.
2. Déterminer le domaine de définition de la fonction g définie par g(x) = e-x ln(1+e2x).
Exprimer g '(x) en fonction de f et justifier que le maximum de g est égal à 2 a½ / (1+a).
e-x est définie sur R ; e2x est positif ou nul ; ln(1+e2x ) est définie sur R. Donc g(x) est définie sur R.
Calcul de g'(x) en posant u = e-x et v = ln(1+e2x).
u' = -e-x ; v' = 2e2x /(1+e2x).
u'v +v'u = -e-x ln(1+e2x) + 2ex /(1+e2x) = -e-x( ln(1+e2x) -2 e2x /(1+e2x)).
En posant t = e2x : g'(t) = -f(t) / t½.
g'(t) s'annule pour f(t)=0 soit t = a soit x = ln a / 2.
Maximum de g : exp(-ln a / 2) ln(1+exp(ln a)) = exp(-ln a½ ) ln(1+ a) = exp(ln a-½ ) ln(1+ a) =ln(1+ a) / a½.
|
|
|
|
Exercice 6.
Calculer les dérivées de :
(x2+1)½. On pose u = 1+x2 ; u' = 2x ; dérivée de u½ = ½u-½ u' =x (x2+1)-½..
ln[ x+(x2+1)½] : on pose u = x+(x2+1)½ ; u'= 1+x (x2+1)-½..
Dérivée de ln u : u' / u = [ 1+x (x2+1)-½] / [x+(x2+1)½] = (x2+1)-½.
En intégrant par partie, déterminer I.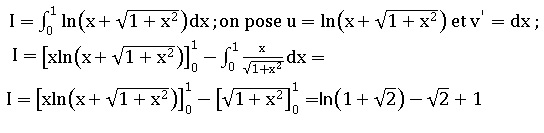
Exercice 7.
On considère un espace de probabilité et deux événements A et B.
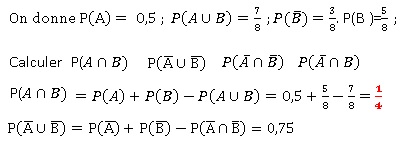
|
|
Exercice 8.
5 % de la population a été vacciné contre une maladie contagieuse. Au
cours d'une épidémie, on constate que la proportion de vaccinés parmi
les malades est de 15 %.. De plus, il y avait une proportion de 30 %
malades parmi les vaccinés.
On considère les événements M =" l'individu est malade" et V=" l'individu est vacciné".
1. Exprimer en langage probabiliste les données de l'énoncé.
La probabilité d'être vacciné est de 5 % : P(V) = 0,05.
PV(M) = 0,30 ; PM(V) = 0,15.
2. Quel est le pourcentage de personnes malades qu cours de cette épidémie ?
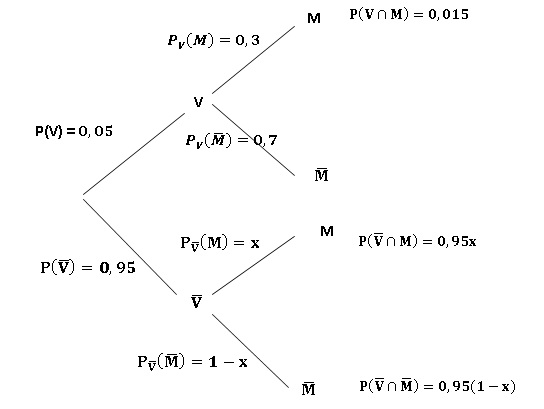
Malades : 0,015 + 0,95 x ;
proportion de malades parmi les vaccinés : 0,015 / (0,015 +0,95x) =
0,15 ; 0,1 = 0,015 +0,95 x soit x = 0,085/0,95 =17 /190 ~0,089 (8,9 %).
3. Quelle est la
probabilité de tomber malade pour une personne non vaccinée ? Exprimer
le résultat sous forme d'une fraction irréductible.
0,95 x = 0,95 * 17 /190 =17 / 200 ~0,085 ( 8,5 %).
4. Le vaccin est-il efficace ?
Non, la probabilité de tomber malade en étant non vacciné est du même
ordre de grandeur que la probabilité de tomber malade en étant vacciné.
Exercice 9.
Possédant au départ un couple de lapins, combien de couples de lapins
obtient-on en douze mois si chaque couple engendre tous les mois un
nouveau couple à compter du second mois de son existence ?
Soit un le nombre de couple au bout du nième mois.
1. Justifier que u1 = u2 = 1 et montrer que pour tout entier naturel n >2 : un+1 = un +un-1.
Au bout d'un mois, on possède toujours un couple, si le couple initial était agé d'un mois : u1 = 1.
Au bout du deuxième mois, le couple initial ne s'est pas encore reproduit : u2 = 1.
Initialisation : au bout du troisième mois, le couple initial donne naissance à un nouveau couple : u3 = 2 =u1 + u2.
Hérédité : on suppose que up+1 = up +up-1 est vraie.
Au cours du mois qui suit, le couple initial donne naissance à un autre couple ainsi que les couples nés au
|
|