Effet de Coriolis,
osillateurs électriques, champ électrostatique
Concours EMIA 2017.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
|
Effet de Coriolis. On désire évaluer l'influence de l'effet de Coriolis sur un point M en mouvement à la surface de la terre.
On définit : R g le repère absolu, le repère géocentrique dans cet exercice.
R t : le repère relatif, repère terrestre dans l'exercice.
1. Rappeler les caractéristiques d'un vecteur.
Un vecteur est caractérisé par son point d'application, sa direction, son sens et sa norme.
On choisit de définir le repère terrestre centré sur le point M étudié
à la surface de la terre. On note l la latitude du point M étudié ( 0°
à l'équateur et 90° au pôle ).
L'axe Mx indique le sud, l'axe My indique l'est et l'axe Mz pointe selon la verticale du lieu et droit vers le ciel.
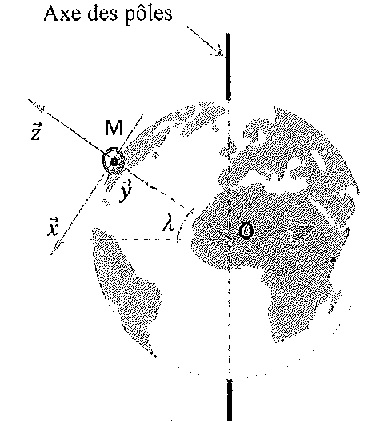
2. Exprimer le vecteur rotation instantané du repère terrestre par rapport au repère géocentrique en fonction de W et l.
Ce vecteur représente la rotation propre de la terre autour de l'axe des pôles.
Coordonnées de ce vecteur ( W cos l ; 0 ; W sin l).
3. Le vecteur vitesse du point M par rapport au repère terrestre a pour coordonnées : Vx, Vy, 0. Justifier la forme de ce vecteur.
Ce vecteur est contenu dans le plan défini par les axes Ox et Oy. Le véhicule reste à la surface de la terre.
4. Déterminer l'expression de l'accélération de Coriolis subie par M en fonction de W, Vx, Vy et l.
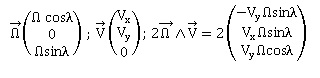
5.
M est situé à 45° de latitude Nord et se déplace à la surface de la
terre à 300 km /h en direction du nord. Evaluer l'accélération de
Coriolis de ce point. Comparer cette valeur à l'accélération de la
pesanteur. Conclure.
Déplacement vers le nord : Vy = 0 ; Vx = V=300 /3,6 =83,3 m/s.
W = 2p / (24 x3600) = 7,26 10-5 rad /s.
ac=2 W V sin l= 2 x7,26 10-5 x83,3 xsin 45 ~8,6 10-3 m s-2.
L'accélération de Coriolis est négligeable devant g = 9,8 m s-2.
|
|
|
|
Oscillateurs électriques.
Le premier circuit étudié comprend un générateur de courant idéal délivrant une intensité i0
= 5 mA, un condensateur de capacité C = 5 µF, une bobine d'inductance L
= 50 mH et de résistance r = 5 ohms et un interrupteur à deux positions.
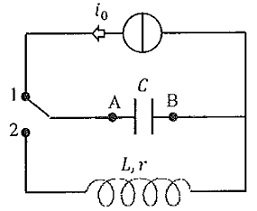
1. L'interrupteur est fermé en position 1 à un instant initial ( origine des temps ) pendant une durée t= 50 ms.
1.1. le condensateur est initialement déchargé. Donner l'expression de la charge qA(t) du condensateur pour la durée de fermeture de l'interrupteur.
qA(t) = i0 t.
1.2. Calculer qA(t) pour t = 50 ms.
qA(t) = 5 10-3 x 50 10-3 = 2,5 10-4 C.
2. Le condensateur ayant la charge calculée à la question précédente, on bascule l'interrupteur en position 2.
2.1. Donner l'équation différentielle vérifiée par qA(t).
Tension aux bornes du condensateur : uAB = qA(t) / C.
Tension aux bornes de la bobine : uAB = Ldi/dt +ri.
i = dqB(t) / dt = -dqA(t) /dt ; di/dt = -d2qA(t) /dt2.
qA(t) / C = Ldi/dt +ri.
qA(t) / C + Ld2qA(t) /dt2 +rdqA(t) /dt =0.
d2qA(t) /dt2 +r /L dqA(t) /dt + qA(t) / (LC)=0.
2.2. Faire un schéma de l'allure de la fonction qA(t) sachant que la décharge du condensateur est pseudo-périodique.

2.3. Comment faudrait-il modifier le circuit pour obtenir une décharge apériodique ?
Mettre en série avec la bobine une résistance suffisamment grande.
3. Pour entretenir les oscillations on réalise un second circuit,
comprenant en plus du condensateur et de la bobine décrits
précédemment, un amplificateur opérationnel idéal et des résistances.
L'amplificateur opérationnel est supposé en fonctionnement linéaire.
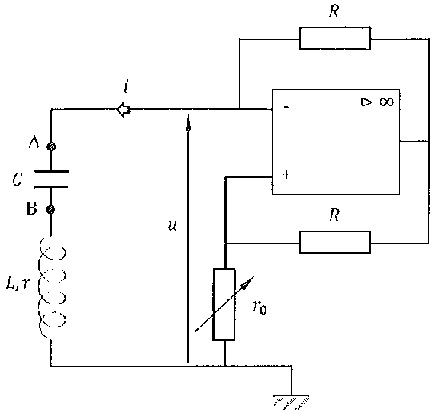
3.1. Montrer que la relation entre la tension u et l'intensité i du courant dans le circuit s'écrit : u = r0 i.
En régime linéaire, les deux entrées de l'amplificateur opérationnel sont au même potentiel.
L'intensité du courant est nulle dans les entrées de l'amplificateur opérationnel.
On note i, l'intensité du courant traversant r0 et R.
Par suite u = r0 i.
3.2. Ecrire l'équation différentielle vérifiée par qA(t).
qA(t) / C +Ldi / dt + ri =r0i =u.
qA(t) / C +Ldi / dt +( r -r0 ) i =0.
3.3. Théoriquement pour quelle valeur de r0 les oscillations ne sont-elles pas amorties dans le circuit ?
r = r0.
3.4. Quelle est alors la période des oscillations ? Faire une application numérique.
T = 2 p( LC)½= 2 x3,14 (0,050 x 5 10-6)½ =3,14 10-3 ~3,1 10-3 s.
|
|
|
|
Champ électrostatique.
Déterminer
en tout point M de l'espace le champ électrostatique créé par un
cylindre infini de rayon r et uniformément chargé avec une densité
volumique de charge noté r.
On distinguera le cas où le point M est à l'extérieur du cylindre et le cas où le point M est à l'intérieur du cylindre.
Justifier chaque étape de votre raisonnement.
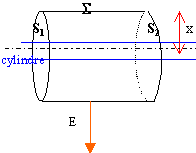
flux
de E à travers S.
En tout point de la surface
latérale
S, par raison de
symètrie, le champ est radial et a même module.
Le flux de ce vecteur à travers la surface
latérale de longueur h
est E
2pxh.
En tout point de S1 ou
S2 le vecteur E est normal au vecteur surface :
le flux de E est nul à travers les 2
bases.
Charge intérieure au cylindre S
de rayon x :
x < r :
Q=px²hr.
x >= r :
Q=pr²hr.
th
de Gauss :
E
2prh
= Q/e0.
x < r : E=
xr
/
(2e0)
x >= r :
E=
r²r
/
(2e0x)
|
|
|