Balistique,
datation potassium argon, masse de Jupiter, ondes
Concours EMIA 2017.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
|
|
Balistique.
Etude
du mouvement d'une bille tirée d'un fusil à air comprimé doté d'un
dispositif hop up annulant les effets de la gravité sur la bille.en
vol. La trajectoire de la bille est rectiligne et horizontale.
1. Enoncer la
seconde loi de Newton.
Dans
un référentiel galiléen, la somme vectorielle des forces extérieures
appliquées au système est égale au produit de la masse du solide par
l'accélération de son centre d'inertie G.
La bille sera donc soumise à une seule force, la résistance de l'air,
colinéaire à la vitesse de la bille, de sens contraire, de norme :
T = ½r S Cx
V2.
r
masse volumique de l'air en kg m-3 ;
S surface qui fait front à l'écoulement, pour une bille de diamètre D,
S = pD2/4
en m2 ;
Cx coeficient de traînée supposé constant.
V vitesse de la bille en m s-1.
2. Donner la
dimension de Cx.
Cx = 2T/ (rSV2)
rSV2 s'exprime en
kg m s-2 ;
T s'exprime en N soit kg m s-2 ; Cx est
donc sans dimension.
3. Montrer que le
mouvement de la bille, sur sa trajectoire horizontale, est régit par
une équation de la forme -dV / V2 = Kdt où K est une
constante à déterminer.
Sur un axe horizontal, orienté dans le sens du mouvement, la seconde
loi de Newton s'écrit :
-
½r S Cx
V2 = m dV /dt.
-dV / V2 =
½r S Cx
/ m dt avec K = ½r S Cx / m.
m =0,2 g ; D = 7,2 mm ; r =
1,225 kg m-3 ; Cx = 0,5 ; vitesse initiale
de la bille en sortie de canon horizontal V0 =120 m /s.
K = 0,5 x1,225 x3,14 x(7,2 10-3)2 x 0,5 / (4 x2 10-4)=6,23 10-2 m-1.
4.
La législation française impose une énergie cinétique de la bille
propulsée inférieure à 2 J pour que ce fusil soit considéré comme une
réplique et non comme une arme. Cette réplique respecte-t-elle la
législation ?
La vitesse , donc l'énergie cinétique de la bille, est maximale en
sortie de canon et vaut :
½mV02 = 0,5 x2 10-4 x1202 =1,44 J.
Cette valeur étant inférieure à 2 J, la réplique du fusil respecte la
législation.
5. Déterminer la
vitesse résiduelle de la bille au bout de 0,1 s de vol.
-dV
/ V2 = Kdt ; une primitive de -1/V2 est 1/V.
1 / V = Kt + constante.
A t = 0, la vitesse vaut V0 ; 1/V0 = constante.
1/V-1/V0 = Kt ; 1 /V -1/120 = 0,0623t.
A t = 0,1 s : 1 / V = 1/ 120 +0,0623 x 0,1 =0,00833 +0,00623 = 0,01456
; V ~ 68,7 m s-1.
6. Déterminer alors
la distance parcourue par la bille dans l'air, toujours en 0,1 s.
La distance est une primitive de la vitesse.
1/V=1/V0
+ Kt ; V = dx/dt = V0 / (1+V0Kt).
Une primitive de 1 /
(1+V0Kt) est
ln
(1+V0Kt) / ( V0K ).
x
= ln
(1+V0Kt) / K + constante.
A t =0, la bille est à l'origine de l'axe.
A t = 0,1s : x = ln(1+120 x0,0623 x0,1) / 0,0623 =8,96 m ~9 m.
|
|
|
|
Datation par la méthode potassium-argon.
Le potassium 4019K est radioactif. Il se
désintègre en donnant de l'argon 4018Ar.
1. Ecrire
l'équation de cette réaction nucléaire.
4019K
---> 4018Ar
+ AZX.
Conservation de la charge : 19 = 18 +Z soit Z = 1.
Conservation du nombre de nucléons : 40 = 40 +A soit A = 0.
4019K
---> 4018Ar + 01e.(
positon).
La période radioactive du potassium 40 est de 1,25 109 ans.
2. Définir la
période radioactive d'un nucléide.
La période radioactive T est la durée au bout de laquelle l'activité
initiale est divisée par deux.
3. Exprimer, en
fonction du temps, le nombre d'atomes de potassium 40 ( nK)
et le nombre d'atomes d'argon ( nAr) présents à une date t
dans un échantillon ne contenant initialement que du potassium 40 ( n0).
nK = n0 exp(-lt) avec lT = ln2.
nAr = n0-nK = n0(1- exp(-lt)).
4. Représenter sur
un même graphique, en fonction du temps, nK et nAg.
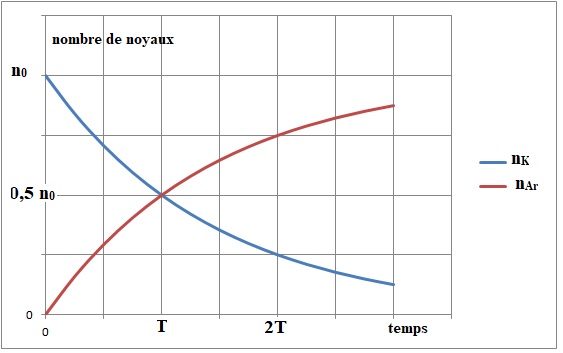
Certaines roches volcaniques contiennent du potassium dont une partie
très faible est du potassium 40 ( 0,01 % du potassium total ).
5. Comment
nomme-t-on les deux autres atomes de potassium, autres que le potassium
40, présents dans la roche sachant qu'ils contiennent respectivement 20
et 22 neutrons ?
Des atomes qui ne diffèrent que par leur nombre de neutrons sont isotopes.
Un géologue analyse un échantillon de ce type de roche et constate la
présence de deux fois moins d'atomes d'argon 40 que de potassium 40. On
suppose qu'au moment de sa formation, cette roche ne contenait pas
d'argon 40.
6. Quel est l'âge
de cette roche ?
nAr /
nK =0,5 =(1- exp(-lt)) / exp(-lt)= 1 / exp(-lt)-1= exp(+lt) -1.
exp(+lt) =1,5 ; t = ln(1,5) / l.
l
= ln2 / T = ln2 /(1,25 109) ~ 5,545 10-10 an-1.
t = ln(1,5) / ( 5,545 10-10
) =7,31 108 ans.
|
|
|
|
Jupiter et un de ses
satellites : Callisto.
Callisto ( diamètre 4820 km, masse m =1,07 1023
kg ) tourne autour de Jupiter sur une orbite supposée circulaire de
rayon r = 1,9 106 km en 16,7 jours.
1. Comment construire un référentiel adapté à l'étude des
mouvements du satellite Callisto ? Justifier.
L'étude est simplifiée dans un référentiel Jupitéro-centrique.
L'origine du repère est le centre de Jupiter et les axes pointent vers
des étoiles lointaines fixes.
2. Si on néglige
l'action des autres astres que Jupiter sur son satellite Callisto,
montrer que la vitesse de Callisto sur son orbite circulaire ne dépend
que de la masse de Jupiter notée M, de la constante de gravitation
universelle et du rayon de l'orbite du satellite.
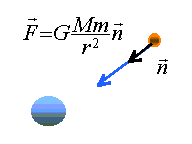 |
Ecrire
la seconde loi de Newton dans le référentiel Jupitero-centrique.
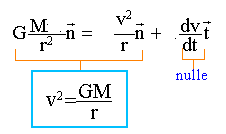
|
3. Après
avoir exprimé la vitesse de Callisto sur son orbite, à partir
de sa définition et en fonction de sa période de révolution
autour de Jupiter, retrouver une formulation de la troisième loi de
Kepler.
période
: durée pour décrire la
circonférence à la vitesse v, norme constante.
2pr = vT.
Elever au carré,
puis remplacer v2 par l'expression ci dessus.
4p2 r2
=GM / r T2.
ou T2 =4p2
/(GM) r3. ( 3 ème loi de
Kepler).
4. En déduire la masse de Jupiter.
T = 16,7 j = 16,7 x 24 xx 3600 = 1,44 106 s ; T2
= 2,082 1012 s2.
r =1,9 109 m ; r3 = (1,9 109)3
=6,86 1027 m3.
T2 / r3 =3,035 10-16 = 4 p2 /(GM).
M = 4 x3,142 / (6,67 10-11 x3,035 10-16)
= 1,95 1027 kg.
Ondes.
1. Donner un exemple d'onde mécanique transversale.
La houle à la surface de l'océan.
2. Donner un exemple d'onde méca,ique longitudinale.
L'onde sonore.
3. Grace à un
vibreur électromécanique fixé à l'extrtémité d'une corde tendue
mesurant 20 m de longueur, on étudie la propagation d'une onde
sinusoïdale le long de cette corde. Le vibreur est alimenté par un GBF
et on admet que les oscillations mécaniques se font à la même
fréquence. Pour tester le dispositif, on débranche le vibreur. On créé
alors manuellement une perturbation à l'extrémité de la corde. On
constate que cette perturbation se déplace le long de la corde tendue
et ayyeint l'autre extrémité au bout de 1,6 s.
3.1. Calculer la célérité de l'onde.
v = L / Dt = 20 / 1,6 =12,5 m /s.
3.2. On admet que
cette célérité est la même pour toutes les fréquences utilisées pour
les expériences, comment qualifie-t-on le milieu de propagation ?
Le milieu de propagation n'est pas dispersif.
3.3.. La fréquence du GBF est réglée sur 40 Hz, calculer la longueur d'onde.
l = v / f = 12,5 / 40 = 0,3125 ~0,31 m.
4. La lumière est-elle une onde mécanique ?
Non, c'est une onde électromagnétique.
5. Décrire une expérience simple permettant de mettre en évidence le caractère ondulatoire de la lumière.
On
réalise une expérience d'interférences lumineuses avec les fentes de
Young éclairées perpendiculairement à leur plan par un faisceau laser
de longueur d'onde l. Les deux fentes fies F1 et F2
sont séparée d'une distance "a". On observe la figure d'interférences
dans un plan parallèle au plan des fentes et situé à une distance D
>>a. On observe une alternance de raies sombres et
brillantes sur l'écran. La raie centrale est brillante.
Un faisceau laser monochromatique de longueur d'onde dans le vide l0=532
nm et se propageant dans l'air, est dirigé vers un tamis à maille
carrée de côté a. On observe sur un écran une figure de diffraction. La
tache centrale est un carré de côté L = 2,66 cm.

|
|
|