Une moto et son
conducteur.
Concours commun polytechnique 2013.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
|
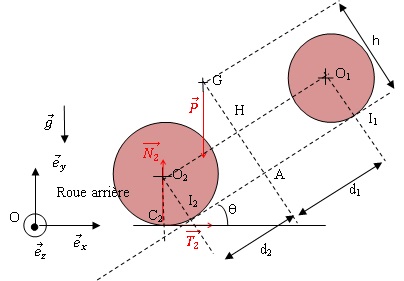
On va étudier quelques mouvements
d’une motocyclette (moto) et de son conducteur. On suppose l’existence
d’un référentiel galiléen auquel est associé un repère orthonormé
direct Oxyz ; la direction Ox est supposée horizontale. L’accélération
due à la pesanteur est notée (pour simplifier les calculs, on pourra
prendre g=10 m s -2). L’ensemble moto + conducteur est de
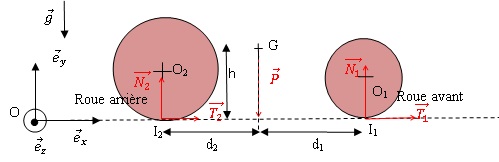
masse M=300 kg, la position du barycentre de cet ensemble est
caractérisée par les distances d 1=0,7 m, d 2=0,4 m
et h=1 m (voir figure ). La roue avant, pneu inclus, de centre O 1,
possède un rayon r 1=0,5 m et un moment d’inertie,
relativement à son axe J 1 =6 kg m 2. La roue
arrière, pneu inclus, de centre O 2, possède un rayon r 2=0,52
m et un moment d’inertie, relativement à son axe J 2 = 10 kg m 2.
Lorsque la moto se déplace, les deux roues en contact avec la chaussée
supposée horizontale, les points de contact des roues avant et arrière
sont notés I 1 et I 2. Les réactions du sol sur les
roues sont respectivement 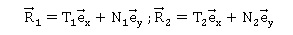 . Le
coefficient de frottement des roues sur le sol es f=0,8 ; il ne sera
pas fait de distinction entre le coefficient de frottement statique et
le coefficient de frottement dynamique. A un instant donné quelconque,
la vitesse instantanée de l’ensemble est v (on se limitera au
cas v >0). De même, on note w1 et w2 , les vitesses de rotation
instantanées des roues avant et arrière. On supposera toujours que les
roues roulent sans glisser sur le sol. De plus, pour les questions
allant de 1.1 à 1.14, on négligera l’action de l’air ambiant sur la
moto et son conducteur. (il peut s’agir, par exemple, d’une phase de démarrage pour laquelle la vitesse n’est pas élevée).
 1.1
1.1 Ecrire les relations de non glissement des roues sur le sol ; en déduire les expressions de w1 et w2 en fonction de v, r 1 et r 2.
Soient I1S un point de la roue au voisinage de I1
et I1R
un point du sol au voisinage de I1. En absence de
glissement les points I1S et I1R
ont la même vitesse. Dans le référentiel du laboratoire :
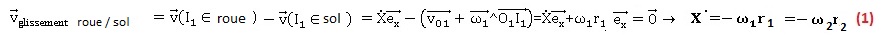 1.2 1.2 On note s1(O 1) et s2(O2), les moments cinétiques en O 1 et O 2 des roues avant et arrière (il s’agit de moments pour un observateur du repère Oxyz). Donner leurs expressions en fonction de J 1, J2, w1 et w2.Les moments cinétiques en O1 et O2 des roues sont les moments cinétiques barycentriques des roues.
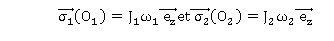 (2)
1.3 (2)
1.3 Montrer que le moment cinétique s(G)
de l’ensemble moto + conducteur relativement au point G, moment pour un
observateur du repère Oxyz, se limite à la somme des moments précédents
(on pourra utiliser le théorème de Koenig faisant référence au repère
barycentrique
Le moment cinétique en G du système moto +conducteur +roues est la
somme des moments cinétiques de trois solides distincts ( roues et moto
+ conducteur, noté sous-système 3). Le moment cinétique barycentrique de la moto +
conducteur de masse m 3 est nul, cet ensemble ne tournant pas.
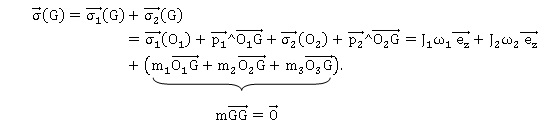 1.4
1.4 En utilisant le théorème de la résultante dynamique, donner deux expressions liant N 1, N 2, T 1, T 2, M, g et v' (accélération instantanée).
On note A 1 et A 2 les actions des axes des roues.
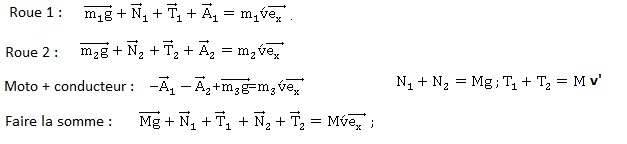 (3)
1.5 (3)
1.5 En utilisant le théorème du moment cinétique, donner une expression liant N1, N2, T1, T2, J1, J2, r1, h, r2, d1, d2 et v'.
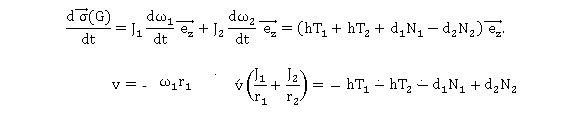 (4) (4)
|
|
|
|
1.6 En appliquant le théorème du moment cinétique à la roue avant, établir une relation entre T1, J1, r1
et v'. (il est à noter que l’articulation de cette roue sur le reste de
la moto est supposée parfaite et que cette roue n’est soumise à aucun
couple).
Le
moteur exerce un couple sur la roue arrière noté G <0
puisqu’il s’agit du couple moteur ; il n’y a pas de couple exercé sur
la roue avant).
Les moments des forces N1, A1 et du poids de la roue, par rapport à O1 sont nuls.
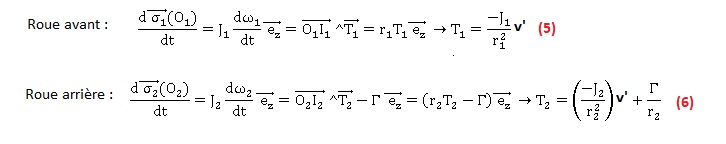
1.7 A partir des relations obtenues, écrire N1, N2, T1, T2 en
fonction de v'.
(3) donne T2 = Mv' -T1 ; T2 = (M+ J1 / r12)v'.
(3) donne N1 = Mg -N2.
Repport dans (4) : v '(J1 /r1 +J2 /r2) = -h Mv ' -d1(Mg-N2) +d2N2 .
N2 = [Mgd1+v '(J1 /r1 +J2 /r2+ h M)] / (d1+d2).
Par suite : N1 = [Mgd2 -v '(J1 /r1 +J2 /r2+ h M)] / (d1+d2).
1.8 Pour une accélération telle que v' / g = 0,1,
montrer que les roues ne décollent pas du sol.
Seule la roue avant peut décoller. Calculons N1 :
J1 /r1 +J2 /r2+ h M =6 /0,5 +10 /0,52 +300 x1 ~331.
N1 = [ 300 x10 x0,4-331] / (0,4 +0,7) ~786 N.
N1 étant positive, la roue avant ne décolle pas du sol.
1.9 De même, montrer
qu’il n’y a pas glissement sur le sol, pour cette accélération.
On calcule |T1| / N1 et on le compare au coeficient de frottement f = 0,8.
T1 = -6 /0,52 = -24 N ; |T1| / N1=24 / 786 = 0,03, valeur inférieure au coefficienr de frottement : il n'y a pas glissement.
1.10 Par application du moment cinétique à la roue
arrière, expliciter la relation liant le couple et l’accélération.
Voir relation (6) ci-dessus.
1.11
On suppose le couple constant, ce qui correspond à une accélération
constante. Exprimer la puissance instantanée P transmise par le moteur
à la roue arrière motrice.
P = -G w2.
Le couple est constant ; w2 est une fonction linéaire ; P croît de manière linéaire.
|
|
|
|
Pour
les questions 1.12 à 1.14, on suppose que le pilote parvient à soulever
du sol la roue avant de son véhicule et on notera θ l’angle
d’inclinaison de O1O2 par rapport à l’horizontale.
1.12 En supposant
négligeable la vitesse de rotation de la roue avant, exprimer le moment
cinétique en G de l’ensemble (il s’agit du moment cinétique pour un
observateur du repère Oxyz).
q est supposé constant, la roue 1 ne tourne pas, la moto et le conducteur ne tourne pas.
Le moment cinétique en G de l'ensemble est celui de la roue arrière.
1.13 Déterminer le moment en G des forces s’appliquant à l’ensemble moto + conducteur.
Le système est soumis à son poids et à l'action du sol sur la roue arrière. Le moment en G du poids est nul.
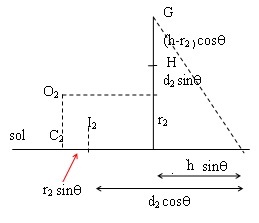
Le bras de levier est d2 cos q+r2 sin q - h sin q sur l'horizontale
et r2 +d2 sin q +(h-r2)cos q sur la verticale.
Somme des moments en G des forces : M= T2 (r2 +d2 sin q +(h-r2)cos q)- N2 (d2 cos q+r2 sin q - h sin q).
1.14 D’après les
deux questions précédentes, donner une équation permettant le calcul de
l’angle θ. Donner la valeur numérique de cet angle, pour v' /g =
0,2 en utilisant le graphe suivant.
Le théorème du moment cinétique conduit à : M= -J2 / r2 v ' = -10 / 0,52 x2 = -38,5 N m.
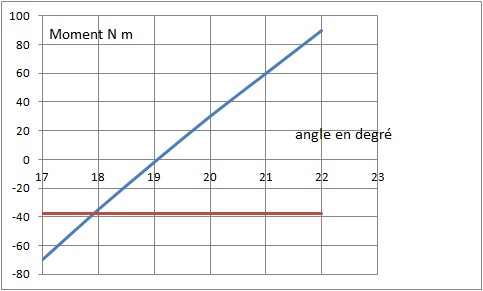 q ~ 18°. q ~ 18°.
|
|
1.15
A partir de cette question, on suppose que la moto roule de nouveau sur
ses deux roues, le moteur exerçant un couple constant sur la seule roue
arrière, couple noté G
< 0. Comme on s’intéresse à une phase où la vitesse v peut être plus
grande que celles des questions précédentes, il est maintenant
nécessaire d’introduire une force supplémentaire de freinage, due à
l’environnement de l’ensemble. Cette force s’écrira 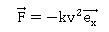 et l’on supposera, pour simplifier, que sa ligne d’action horizontale
passe par le point G. Etablir l’équation différentielle pour v .
et l’on supposera, pour simplifier, que sa ligne d’action horizontale
passe par le point G. Etablir l’équation différentielle pour v .
1.16 Montrer qu’il existe, pour la vitesse v, une valeur limite vl dont on donnera l’expression en fonction du couple moteur et des autres paramètres.
1.17 Montrer que l’équation précédente peut s’écrire sous la forme v ' +av2 = avl2. On précisera l’expression de la constante a en fonction de k, M, J1, J2, r1 et r2.
1.18
En supposant que la vitesse est nulle à l’instant 0,=t établir la
solution de l’équation précédente. Pour cela, on pourra introduire le
changement de fonction suivant :
u =vl / (vl-v) .
La relation (3) conduit à : N1 +N2 = Mg.
T1+T2-kv2 =Mv '.
Le moment en G de cette force de frottement horizontale est nul. Les relations (5) +(6) donnent :
T1+T2 = -[J1 / r12 +J2 / r22] v ' +G / r2.
-[J1 / r12 +J2 / r22] v ' +G / r2 = Mv ' +kv2.
G / r2 -kv2=M [1 +J1 / r12 +J2 / r22] v ' .
G /(k r2 ) =v2+M / [k [1 +J1 / r12 +J2 / r22]] v ' .
On pose a = k / [M [1 +J1 / r12 +J2 / r22]].
a G /(k r2 ) =av2+v '.
S'il existe une vitesse limite, la dérivée par rapport au temps de la vitesse limite est nulle.
G / r2 -kvl2=0 ; vl = [G /(r2k)]½.
L'équation devient : v ' +av2 = avl2.
v ' + a(v2-vl2) =v' + avl2( v2/ vl2-1) On pose u = v / vl.
u ' +avl2(u2-1)=0 ; u' /u2-1)+avl2 =0
1/ (u2-1) =0,5 / (u-1) -0,5 / (u+1).
0,5du /(u-1)-0,5 du /(u+1) = -avl2 dt.
0,5ln(u-1) - 0,5ln(1+u) = -avl2t + Constante.
- arcth u= -avl2t + Constante.
u = th( avl2t + Constante).
La vitesse initiale étant nulle, la constante d'intégration est nulle.
u = th( avl2t) ; v = vl th(avl2t).
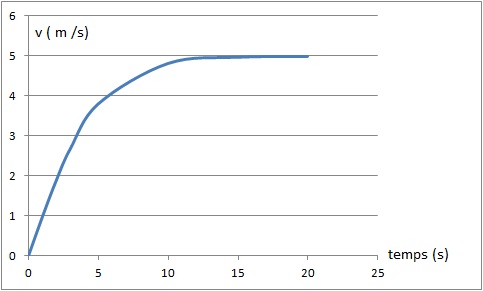
La résolution de l'équation différentielle conduit à l'existence d'une vitesse limite.
|
|