Les ponts : oscillations, dilatation thermique, corrosion , BTS travaux publics 2017.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.



. .
.
.


Oscillations d'un pont.
A. Etude du comportement d'un système oscillant.
Lorsqu'on met en oscillation un système solide-ressort horizontal à l'aide d'un banc à coussin d'air et qu'on enregistre l'amplitude du mouvement à l'aide d'un sytème informatisé, on constate que l'amplitude ne semble pas varier sur une durée de 0,80 s.
1. Qualifier le type de régime oscillatoire associé à cet enregistrement. Donner l'allure de l'enregistrement sur une durée beaucoup plus longue.
Mouvement oscillatoire libre non amorti. Oscillations sinusoïdales.
Sur une durée plus longue, du fait d'un faible amortissement, l'amplitude diminue.
Un variateur électroniquepermet de faire varier le débit d'air.
2. Sur quel paramètre du banc à coussin d'air faut-il agir pour conduire à cet enregistrement ?
Un variateur électronique permet de faire varier le débit d'air. Si celui-ci est important, l'oscillateur est très peu amorti.

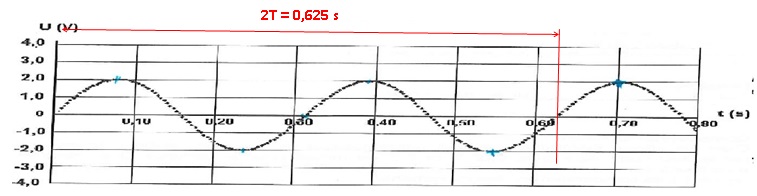
 3. Déterminer la valeur de la période propre T0 de cet oscillateur.
2T0 ~0,625 s ; T0 ~0,312 s.
On réalise l'expérience suivante : on accroche deux pendules simples à un fil tendu horizontalement entre deux points fixes M et N. Le pendule 1 a une longueur fixe L0 = 20 cm et la longueur du pendule 2 est variable.

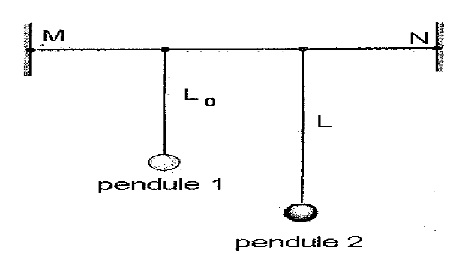
On met en mouvement le pendule 2 et on constate que le pendule 1 se met à osciller. On répète l'expérience en modifiant la longueur L du pendule 2 et on mesure l'amplitude angulaire maximale am du pendule 1. Le graphe ci-dessous reproduit l'allure de l'évolution de l'amplitude du pendule 1 lorsqu'on fait varier la longueur du pendule 2.


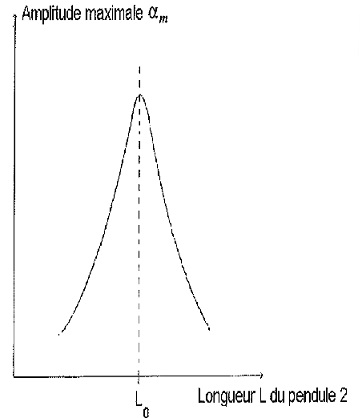4. Une montre battant la seconde serait-elle adaptée pour vérifier la période propre du pendule 1 ? Si oui, détailler le protocole à suivre, sinon expliquer pourquoi.
La période du pendule 1 est de l'ordre de  :
2 p (L0/g)½ = 2 x3,14 (0,20 /9,8)½~0,9 s. Une montre battant la seconde est adaptée.
Utilisercette montre et mesurer la durée de 10 périodes par exemple.
5. Dans l'expérience précédente, identifier l'excitateur et le résonateur.
Excitateur : pendule 2, de longueur variable.
Résonateur : pendule 1 de longueur fixe.
6. Expliquer en quoi cette expérience illustre le phénomène de résonance mécanique.
Lorque la fréquence de l'excitateur est proche de celle du résonateur ( pendules de même longueur ), l'amplitude angulaire du résonateur est maximale et très grande si l'amortissement est faible.

B. Oscillations du pont de Tacoma.
Le tablier du pont effectuait des oscillations de torsion avec une période de l'ordre de 5 s. Une des hypothèses émises pour expliquer sa destruction a été un phénomène de résonance entre le pont et les tourbillons d'air créés dans le sillage du tablier. Pour vérifier cette hypothèse, une expérience  a été conduite sur une maquette.
Paramètres
 Pont de Tacoma
 Maquette
Vitesse du vent U
 19 m /s
 A définir
Largeur du pont B
 12,2 m
 6,1 cm
Période d'oscillation du pont T
 5,0 s
 0,094 s
7. Calculer la vitesse réduite dans le cas du pont de Tacoma ppuis montrer que pour respecter les règles de similitudes, il faut régler la souflerie de manière à obtenir un vent de vitesse 5 m/s pour que la maquette simule la destruction du pont.
Ur = T U/ B =5,0 x 19 / 12,2 =7,8.
L'expérience avec la maquette doit avoir la même vitesse réduite que dans le cas réel de destruction du pont.
7,8 = 0,094 Usoufflerie / 0,061 ; Usoufflerie =7,8 x0,061 / 0,094 ~5,0 m /s.
Les toutbillons qui se forment dans le tablier ont une période donnée par le nombre de Strouhal St qui dépend de la forme du tablier.
St = 0,11 dans ce cas. St = D / (UT) avec D épaisseur du pont en mètre, U, vitesse du vent en m/s et T la période d'oscillation en seconde.
Sachant que la maquette a une épaisseur de 1,2 cm, montrer que la période des tourbillons d'air ne perment pas l'entrée en réssonance de la maquette, ne confirmant pas l'hypothèse émise pour expliquer la destruction du pont.
T = D / (StU) = 0,012 / (0,11 x 5) ~0,022 s, 4 fois moins que la période de la maquette.
Pour qu'un phénomène de résonance se produise, il faut que la période propre des oscillations du pont soit voisine de la période des tourbillons de vent. L'hypothèse du phénomène de résonance est a rejeter.
8. Une autre hypothèse explicative de l'accident propose une mise en résonance du tablier lié à un changement d'inclinaison du vent. Expliquer pourquoi cette hypothèse semble cohérente.
Le vent souflant sur le tablier créé des tourbillons au dessus et au dessous de celui-ci. Ces tourbillons engendrent des pressions sur le tablier qui s'annulent sur une structure immobile.
Par contre sur un pont mis en mouvement par les tourbillons, les pressions ne s'annulent plus et ont tendance à tordre la structure. Cette torsion modifie davantage l'écoulement du vent autour du pont, ce qui amplifie la torsion et ainsi de suite jusqu'à l'effondrement.
..


La dilatation thermique des tabliers.
10. Expliquer dilatation linéaire d'un matériau.
La dilatation est l'augmentation de volume d'un corps lorsque sa température croît. Si le corps est long, sa dilatation sera surtout visible dans le sens de la longueur, on parle de dilatation linéaire.
11. Que pourrait-il se passer pour le béton, armé d'armatures en acier, si les coefficients de dilatation du béton et de l'acier  étaient très différents.
Les allongements ou rétractations de l'acier et du béton seraientt très différents, ce qui entrainerait des fissures du béton armé.
12. Dans quelles conditions de températures le tablier du pont va t-il se rétracter ou se dilater ?
Quand la température augmente, le pont se dilate ; quand la température diminue, le pont se rétracte.
13. En supposant le tablier du pont comme constitué d'un matériau uniforme, calculer la variation de longueur pour les conditions extrèmes de températures dans le cas du viaduc de Millau. On prendra comme coefficient de dilatation a = 1,2 10-5 °C-1.
Teùmpérature la plus basse enregistrée -17,5°C, température la plus haute 37,5°C. Longueur du tablier L0 =2460 m
DL = a L0DT = 1,2 10-5 x2460 x(37,5 +17,5) ~1,6 m.
14. Justifier l'intérêt de la pose de joints de dilatation entre la route sur les collines et le tablier.
Ces joints  évitent un effort trop important entre la route et le tablier en début de colline.
Parmi les modèles de joints suivants, c'est le modèle B qui a été choisi.

15. Donner un argument justifiant ce choix.
Le pont peut également se dilater en largeur. Le modèle B permet une dilatation en longueur et en largeur.


Corrosion des structures métalliques.
16. Pourquoi l'huile se dispose-t-elle au dessus de l'eau ?
L'huile et l'eau ne sont pas miscible et l'huile est moins dense que l'eau.
17. Au vu des expériences proposées, quels sont les facteurs qui ont une influence sur la formation de la rouille ?
Des clous en acier sont dégraissés et placés dans différentes boîtes de Pétri.
Boîte 1 : on ajoute quelques cristaux de chlorure de calcium anhydre qui ont la propriété d'absorber la vapeur d'eau. Au bout de 24 heures, aucun changement n'est observé.
Boîte 2 : on recouvre les clous avec de l'eau bouillie ( pour la désaérer)  et de l'huile qui forme une  couche au dessus de l'eau empéchant le contact avec l'air. Au bout de 24 h, des taches brunes de rouille sont visibles.
Boîte 3 : on recouvre les clous avec de l'eau déminéralisée. Au bout de 24 h, des taches brunes de rouille sont encore plus visibles.
L'eau et le dioxygène sont donc des facteurs favorisant la formation de la rouille.
18. Quelles sont les dispositions prises sur le viaduc qui permettent de limiter la formation de la rouille ?
La structure du caisson est peinte et munie d'un système de ventilation d'air sec. Un système récupère les eaux de ruissellement.
19. Ecrire la demi-équation électronique du couple Fe2+ / Fe. Préciser quelle est l'espèce oxydante et l'espèce réductrice.
Fe2+  2e- = Fe.
Fe2+ gagne des électrons, c'est l'oxydant du couple.
Fe cède des électrons, c'est l'espèce réduite du couple.
L'oxydation du fer met en jeu trois réactions.
Formation d'ion fer (II) avec dégagement de dihydrogène.
Oxydation des ions fer (II) par le dioxygène de l'air et formation d'hydroxyde de fer (III) Fe(OH)3.
Transformation de Fe(OH)3 en Fe2O3.
20. Indiquer dans l'ordre les équations bilans des trois réactions mises en jeu dans la corrosion du fer.
Fe + 2H+ --> Fe2+ +H2.
4Fe2+ +4O2+10H2O --> 2Fe(OH)3 +6H+.
2Fe(OH)3 --> Fe2O3 +3H2O.
Certaines peintures anti-corrosion contiennent du minium de plomb Pb3O4.
21. Dans les conditions de pH de la peinture, les couples mis en jeu sont Pb3O4 / PbO et FeO/Fe, expliquer la formation d'une couche protectrice constituée d'oxyde de plomb PbO et d'oxyde de fer FeO.
Oxydation du réducteur le plus fort, le fer : Fe +H2O --> FeO +2H++ 2e-.
Réduction de l'oxydant le plus fort Pb3O4 : Pb3O4 +2H++2e- --->3 PbO + H2O.
Bilan : Fe + Pb3O4 --->FeO + 3 PbO.

 .


  

menu