Les matériaux à
changement de phase.
BTS Travaux Publics 2016.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Les matériaux à changement de phase (MCP) ont la capacité de stocker de
la chaleur avant de la
restituer.
Thermique (A)
Les matériaux à changement de phase
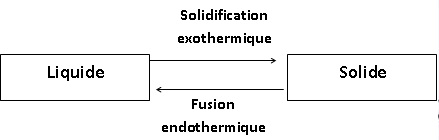
1) Sur le schéma ci-dessous faire figurer au-dessus de chaque
flèche le nom des changements d’état. Indiquer lequel correspond à un
changement d’état exothermique et lequel correspond à un
changement d’état endothermique.
2) Pourquoi l’eau à
la pression atmosphérique ne peut-elle pas être utilisée comme MCP pour
la
régulation thermique des bâtiments ?
La température de changement d'état des MPC doit se situer entre 19 et
27°C. La température de changement d'état de l'eau est trop basse.
Détermination de caractéristiques
thermiques du béton
On suit le protocole suivant avec un béton de masse volumique rb = 2400 kg.m-3.
- Introduire une masse me d’eau dans le calorimètre.
- Mesurer la température qi
de l’ensemble.
- Introduire dans le calorimètre un morceau de béton de masse m
préalablement placé dans un bain marie à la température q.
- A l’équilibre thermique, relever la température finale qf de l’ensemble.
Dans des ouvrages spécialisés, on trouve que pour cette formulation du
béton, la valeur de la capacitéthermique massique du béton attendue se
situe autour de c = 980 J.kg-1.K-1.
L’exploitation des mesures expérimentales obtenues avec le protocole
conduit à une valeur assez
différente.
3) Expliquer sans
calcul d’où peut provenir cet écart.
Le calorimètre n'est pas parfaitement adiabatique : il y a des échanges
de chaleur entre le calorimètre et l'extérieur.
Détermination de la conductivité thermique.
On suit maintenant le protocole expérimental suivant pour déterminer la
conductivité thermique d’un bloc de béton de masse volumique rb = 2400 kg.m-3,
de surface S et d’épaisseur e.
- L’échantillon de
béton est placé entre deux plaques d’aluminium dans une enceinte isolée
partiellement de l’extérieur.
- Une face de ce matériau est chauffée par effet Joule à l’aide d’une
résistance chauffante.
- Cette énergie électrique est transférée à l’échantillon de béton.
- L’autre face est refroidie grâce à une cellule Peltier.
- Deux sondes thermométriques repèrent la température de chaque face du
béton.
- Le ventilateur permet d’évacuer la chaleur dissipée par la cellule
Peltier.
- Une fois le régime stationnaire établi les températures q1 de la face
chaude et q2
de la face froide
du béton sont relevées.
- On note R la résistance thermique de cet échantillon de béton.
4)
Quel mode de transfert thermique est mis en jeu dans le bloc de béton ?
La conduction.
5) Rappeler la
relation liant le flux thermique F et la différence de température Dq
dans le cas d’une paroi plane, en précisant les unités des grandeurs
utilisées.
F = Dq / R avec R = e / (lS).
F :
watt ; Dq : K ; R = K
W-1. e : épaisseur (m) ; S : surface (m2) ;
l
conductivité thermique ( W K-1 m-1)
6) Expliquer soigneusement pourquoi
ce dispositif expérimental permet d’accéder à la mesure de la
résistance thermique du béton.
En régime permanent la puissance électtrique P=UI est connue ( mesure
de U et de I à l'aide respectivement d'un voltmètre et d'un ampèremètre
). La différence de température est également déterminée.
7) A partir des des
données expérimentales suivantes, justifier que le flux thermique a
pour valeur F = 6,00 W.
U(V)
|
I(A)
|
S(cm2)
|
q1 °C
|
q2 °C |
e(mm)
|
12,00
|
0,500
|
64,0
|
29,7
|
27,5
|
5,00
|
F = UI = 12,00 x0,500=6,00
W.
8) Montrer que les
mesures expérimentales précédentes permettent de retrouver une valeur
de la
conductivité thermique, l,
du béton, proche de celle proposée dans les données.
l = e F / (Dq S) = 5,0010-3
x6,00 / (2,2 x64,0 10-4)=2,13
W K-1 m-1.
Etude d’une association MCP-béton.
(Ajout d’un panneau de MCP sur un mur)
On s’intéresse à un mur composé pour grande partie de béton et de
coefficient de transmission thermique U = 0,660 W.m-2.K-1.
9) Rappeler la
relation liant la résistance thermique surfacique rmur et le
coefficient de transmission
thermique.
9) Rappeler la relation liant la résistance thermique surfacique rmur
et le coefficient de transmission
thermique. Calculer rmur.
rmur = 1 / U = 1 / 0,660=1,515 ~1,52 m2 W-1 K.
On plaque sur toute la surface du mur un panneau à inertie thermique
(épaisseur e’ = 5 mm) contenant un MCP.
La conductivité thermique du panneau est estimée à l’ = 0,180 W.m-1.K-1.
Ce panneau contient 2,70 kg de paraffine.
10) Calculer la
résistance thermique surfacique globale rg et en déduire le
nouveau coefficient de
transmission thermique Ug de l’association ainsi constituée.
rg =rmur +e / l' =1,515 + 5 10-3
/ 0,180 = 1,543 ~1,54 m2 W-1 K.
Lors
d’un essai en laboratoire, le panneau à inertie thermique de surface S
= 1 m2 est soumis à une variation de température de 18°C à
24°C.
Sur le site constructeur, on peut voir le diagramme ci-dessous.
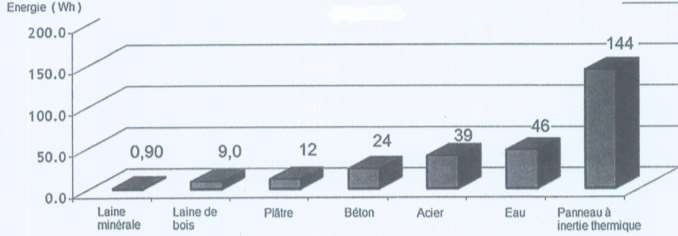
• Comparaison du stockage thermique de différents matériaux avec un
panneau à inertie thermique pour une même épaisseur (5 mm)
[10°C - 24°C]
|
|
|
11) A l’aide du diagramme précédent,
montrer que pour cette variation de température, l’énergie stockée dans
le panneau est due pour plus de 85% à l’énergie mise en jeu par la
fusion de la paraffine que le panneau contient (on rappelle que le
panneau contient m = 2,70 kg de paraffine).
144 Wh = 144 x3600 J = 5,184 105 J= 518,4 kJ.
Chaleur latente massique (enthalpie) de fusion de la paraffine : Lf
= 166 kJ.kg-1.
166 x 2,70 =448,2 kJ.
448,2 / 518,4 = 0,865 ( 86,5 %).
12) Montrer que
l’épaisseur de béton qui, à surface égale, permettait un stockage
d’énergie équivalent à celui d’un panneau à inertie thermique est
d’environ 3 cm.
5 x144 /24 =30 mm = 3,0 cm.
13) Conclure quant
à l’intérêt de l’ajout d’un panneau à inertie thermique sur le mur (on
s’intéressera aux aspects d’isolation et de stockage thermiques).
Très bon isolant thermique.
Bon stockage ( et donc de déstockage ) d'énergie.
Une étude expérimentale en comparant un béton de référence (masse
volumique rb
= 2400 kg.m-3) avec un béton contenant 5% en volume de MPC
(masse volumique rMCP
= 770 kg.m-3) a conduit aux graphes suivants.
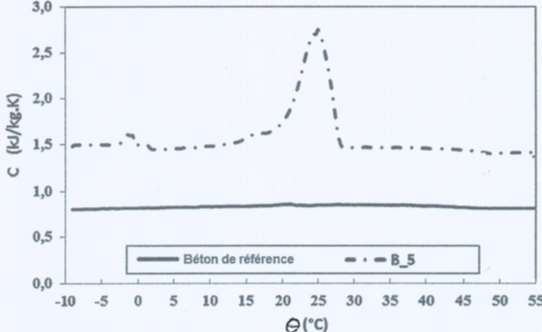
• Evolution de la capacité thermique massique en fonction de la
température
(Lecture : B_5 signifie que 5% du volume total est constitué de MCP).
• Évolution de la conductivité thermique en fonction de la composition
du béton
(Lecture : B_5 signifie que 5% du volume total est constitué de MCP)
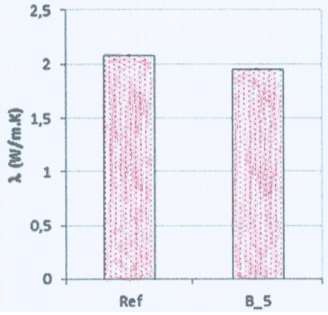
14) Justifier que l’incorporation d’un MCP dans le béton, permet
d’augmenter son inertie thermique par rapport au béton de référence.
La conductivité thermique est légérement plus faible que dans le béton
de référence.
Par contre à 25°C, la capacité thermique massique est près de 4 fois
supérieure à celle du béton de référence. L'inertie thermique d'un
béton avec MPC est bien plus grande que celle d'un béton classique.
|
|
|
|
Chimie organique.
Identification des paraffines utilisables comme MCP
1) En s’aidant du
graphe suivant, proposer, en justifiant le choix, un nom et une formule
chimique pour chacune des paraffines constituant les MCP respectivement
:
• Variations des températures de fusion des alcanes linéaires en
fonction du nombre n, d’atomes de carbone qui les constituent.
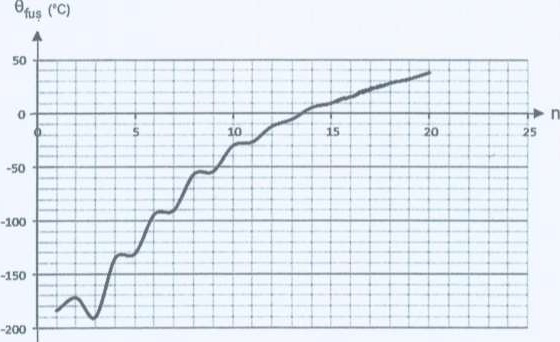
- Pour le confort thermique des bâtiments.
La température de changement d'état doit se situer entre 19°C et 27°C :
17 atomes de carbone.
C17 H36, heptadécane.
- Pour la prévention de la formation du verglas sur les routes.
La température de changement d'état doit se situer entre 0°C et -5°C :
14 atomes de carbone.
C14 H30, tétradécane.
Étude de
l’encapsulant du MCP d’un panneau à inertie thermique.
Il est possible de déterminer la masse molaire moléculaire d’un
polymère à partir de différentestechniques (diffusion de la lumière,
mesure de viscosité, fractionnement par dissolutions sélectives…).
On a déterminé une masse molaire moyenne Mpolyéthylène =
56,0 kg.mol-1 pour le polyéthylène, polymère obtenu à partir
de l’éthylène de formule semi-développée CH2 =CH2
.
2) L’éthylène
(éthène) fait-il partie de la famille des alcanes ? Justifier.
Formule brute d'un alcane CnH2n+2 ; formule brute
de l'éthylène C2H4 ; l'éthylène n'est pas un
alcane.
3) Expliquer
pourquoi l’éthylène est polymérisable.
L'ouverture de la double liaison permet la formation de liaison
covalente entre les molécules d'éthylène.
4) Écrire
l’équation de la réaction traduisant la synthèse du polyéthylène à
partir d’éthylène.
n (H2C=CH2) --> -[-CH2--CH2-]- n fois
5) Montrer que le degré de polymérisation du polyéthylène vaut 2000.
M(éthylène) = 2 x12 +4 = 28 g/mol ;
degré de polymérisation : 56 x1000 /28 =2000.
Formule du polypropylène
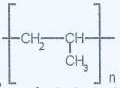
6) Donner la formule brute et la formule semi-développée du monomère correspondant.
C3H6 ; propène , H2C=CH-CH3.
|
|