Equation
différentielle, étude de fonction.
BTS groupe B 2017.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Antilles Métropole.
Dans un régulateur de niveau, la hauteur de liquide varie en fonction du temps. On note h(t ) la
hauteur (en mètre) atteinte par le liquide à l’instant t (en heure).
On suppose que h est une fonction de la variable réelle t définie et deux fois dérivable sur [0 ; +∞[.
A. Résolution d’une équation différentielle.
Une étude mécanique montre que la fonction h est solution de l’équation différentielle
(E) 10y′′ +3y′ +0,2y = 1,
où y est une fonction inconnue de la variable réelle t , définie et
deux fois dérivable sur [0 ; +∞[, y′ la fonction dérivée de y et y′′ sa
fonction dérivée seconde.
1. a. Résoudre dans R l’équation 10r 2 +3r +0,2 = 0.
Discriminant D = 32 -4 x0,2 x10 =1.
Solutions r1 = (-3+1) / 20 = -0,1 ; r2 = (-3-1) / 20 = -0,2.
b. En déduire les solutions de l’équation différentielle (E0) :
10y′′ +3y′ +0,2y = 0.
y = A exp(-0,1t) +B exp(-0,2t).
Les
conditions initiales du système mécanique conduisent à poser h(0) = 8
et h′(0) = 0. Un logiciel de calcul formel fournit l’expression
suivante de la fonction h.
y = 6e− 0,1t −3e-0,2t+5.
Quelle est la hauteur du liquide au bout de deux heures ? Arrondir au dixième.
h(2) =6 e-0,2 -3 e-0,4+5=7,9 m.
B. Étude de fonction.
On considère la fonction h définie et dérivable sur [0 ; +∞[ par :
h(t ) = 6e−0,1t −3e−0,2t +5.
On note C la courbe représentative de h dans un repère orthogonal et on appelle D la droite d’équation y = 5.
1. a. Justifier que la limite de h(t) est égale à 5 lorsque t tend vers l'infini.
e0,1 t tend vers l'infini quand t tend vers l'infini ; 1 / e0,1t tend vers zéro qund t tend vers l'infini.
e0,2 t tend vers l'infini quand t tend vers l'infini ; 1 / e0,2t tend vers zéro qund t tend vers l'infini.
Par somme de limite h(t) tend vers 5 quand t tend vers l'infini.
b. Interpréter graphiquement le résultat précédent.
La droite d'équation y = 5 est asymptote à la courbe C.
2. Déterminer une expression de h′(t ).
h'(t) = -0,6 e-0,1t +0,6 e-0,2t=0,6 (-e-0,1t +e-0,2t).
3. Un logiciel de calcul formel fournit le résultat suivant, qui est admis : l’ensemble
des solutions de l’inéquation h′(t ) <0 est l’intervalle [0 ; +∞[.
Dresser le tableau de variation de la fonction h sur l’intervalle [0 ; +∞[.
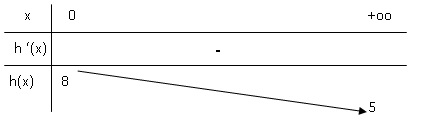
|
|
|
Étude locale.
On rappelle que la fonction h est définie et dérivable sur [0 ; +∞[ par :
h(t ) = 6e−0,1t −3e−0,2t +5.
On note C la courbe représentative de h dans un repère orthogonal et on
appelle T la tangente à la courbe C au point d’abscisse 0.
Un logiciel de calcul formel affiche la partie régulière du
développement limité à l’ordre 2 de fonction h au voisinage de zéro.
Polynôme de Taylor de h(t) : 8-0,03t2.
1. Le développement limité de la fonction h, à l’ordre 2, au voisinage de 0 est :
8-0,3t2. Faux.
8-0,03 t2 +t2e(t) avec e(t) tend vers zéro quand t tend vers l'infini. Faux.
8-0,03 t2 +t2e(t) avec e(t) tend vers zéro quand t tend vers zéro. Vrai.
0,03 t2 +t2e(t) avec e(t) tend vers zéro quand t tend vers zéro. Faux.
2. Une équation de la tangente T est :
y = -0,03t2 ; faux ; y = 8-0,03t2 ; faux ; y = 8 ; vrai ; y = 8 t ; faux.
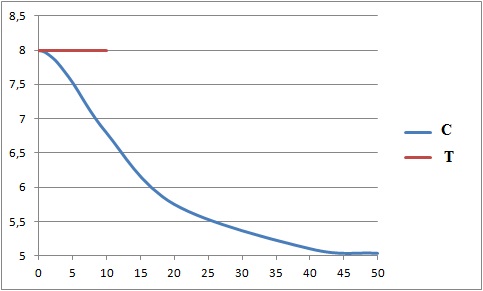
3. Étudier la position relative, au voisinage du point d’abscisse 0, de la courbe C et de la tangente.
Au voisinage de zéro h(t) -y = 8-0,03 t2 +t2e(t)-8 = -0,03 t2 +t2e(t), négatif.
La tangente T est au dessus de la courbe C au voisinage de zéro.
|
|