Puits canadien,
thermique, acoustique, chimie organique,
Bts EEC 2017.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
|
Le puits
canadien est une solution géothermique de surface qui permet
de tempérer, à moindre coût, l’air de ventilation d’une maison.
Le principe de fonctionnement est très
simple.
À une profondeur d’environ deux
mètres sous terre, la température est presque
constante toute l’année (environ 13°C sous nos latitudes, rendant
possible des
échanges thermiques.
En effet, en faisant circuler
de
l’air dans un système de tuyauteries enfoui dans la terre, un échange
thermique
va s’effectuer entre la terre et l’air.
Il sera ainsi possible
d’augmenter la température de l’air d’une dizaine de degrés Celsius en
hiver et
de diminuer d’autant en été.
Un ventilateur est utilisé pour
extraire cet air du système de tuyauteries et l’insuffler dans la
maison pour
en assurer la ventilation.
On utilise un système de
ventilation de type VMC (ventilation mécanique contrôlée) pour extraire
l’air
vicié de la maison.
Thermique
Transfert thermique
On cherche à mesurer le gain
énergétique
apporté par le puits canadien, pendant la période hivernale de
chauffage, qui
dure environ six mois.
1- Étude sans le puits canadien.
Dans cet exercice, on néglige
les pertes
thermiques intervenant par le sol.
Données :
- La maison, disposant d’une porte (0,90 m x 2,10 m) et
de six fenêtres (1,10 m x 1,10 m)
non représentées sur le schéma précédent, a pour dimensions :
longueur L=12 m, largeur
ℓ =10 m et hauteur h=2,5 m.
- En période hivernale, la température intérieure θi
souhaitée est de l’ordre de 20,0°C et la température extérieure moyenne
est θe
= 3,0°C.
- résistances thermiques surfaciques superficielles intérieure et
extérieure :
rsi = 0,130 m2K.W-1
et rse = 0,050 m2K.W-1
- Flux thermiques en période hivernale, à travers toutes les ouvertures
Φ2 = 171 W et à travers le toit Φ3 = 204 W
- De l’intérieur vers l’extérieur, les murs sont constitués des
matériaux suivants :
|
Matériaux
|
Conductivité
thermique λ (W.m-1.K-1)
|
Epaisseur e (cm)
|
|
Plâtre
|
0,55
|
1,0
|
|
Isolant
|
0,030
|
16,0
|
|
Béton
|
1,89
|
15,0
|
1) Donner
l’expression littérale de la résistance thermique surfacique r1
des murs en fonction des épaisseurs et des conductivités thermiques. Calculer sa valeur pour les murs de la
maison.
r1 = eplatre / lplatre + eisolant / lisolant +ebéton / lbéton +rsi
+rse.
r1 = 0,01 /0,55 +0,16 /0,030 +0,15 / 1,89 +0,130 +0,050
=0,0182+ 5,333+0,0794+0,18.
r1~5,6 m2K.W-1.
2) Donner l’expression littérale du
flux thermique surfacique φ1,
à travers les murs, en fonction des températures et de r1. Calculer sa valeur.
f1
= (qi-qe) / r1
=(20-3) / 5,6=3,03 ~3,0 W m-2.
3) Donner
l’expression littérale du flux thermique Φ1, à
travers les murs. Calculer sa valeur.
F1
= f1 Smur
=3,03 [(12+10+12+10)x2,5-0,90x2,10-6x1,10x1,10]= 3,03 x100,85 =305,6~3,1 102 W.
4) Donner
l’expression littérale du flux thermique total Φ, à travers
l’ensemble des parois (murs, ouvertures et toit) de la maison. Montrer que sa valeur est de 7,0.102
W.
F = F1+F2+F3 = 305,6
+171+204=681 ~6,8 102 W.
5) Déterminer (en joules) la valeur de l’énergie E
utilisée par les
appareils de chauffage en une journée afin de compenser les pertes à
travers
l’ensemble des parois de la maison.
E = 6,8 102 x24 =1,63 104 Wh ~16 kWh ( 1,63 104 x3600 ~5,9 107 J)
Pour une bonne aération, l’air de la maison
doit être renouvelé toutes les heures.
Pour une journée,
l’énergie E’
nécessaire pour chauffer ce volume d’air de 3,0°C à 20,0°C vaut 1,59.108 J.
6) En déduire l’énergie totale
Etotale, utilisée par les
appareils de chauffage en une journée pour maintenir une température
intérieure
de 20°C avec l’aération.
5,9 107 +1,59 108 ~2,2 108 J.
2- Étude
avec le puits canadien.
On met en marche le système de
ventilation.
L’air entre dans le puits
canadien à la
température de θ1 = 3,0°C, se réchauffe en circulant dans la
canalisation enterrée et arrive à l’intérieur de la pièce à une
température de θ2
= 11,0°C.
Données :
- Masse volumique de l’air : ρair = 1,30 kg.m-3
- capacité thermique massique de l’air : cair = 1,00.103
J.kg-1 K-1.
Pour obtenir une bonne
aération, on veut
renouveler l’air de la maison toutes les heures.
1) Montrer
que la masse d’air qui doit circuler dans la canalisation, en
une journée, est environ égale à 9360 kg.
Volume de
la maison V = 12 x10x2,5 = 300 m3.
Masse d'air à renouveler : 24 x 300 x 1,30 = 9360 kg.
2) Montrer
que la valeur de l’énergie thermique E’’,
transférée à cette masse d’air lorsqu’elle passe de 3,0°C à 11,0°C dans
la
canalisation du puits canadien, est d’environ 7,49.107 J.
E" = 9360 x1,00 103 x(11-3) =7,49
107 J.
3) Comparer
la valeur de l’énergie E’ donnée à la question
1-6) à la valeur de E’’, énergie économisée grâce au puits canadien. Le
puits apporte-t-il un gain d’énergie
significatif ?
Justifier la réponse à l’aide d’un
calcul.
E" / E' = 7,49 107 / (1,59 108) ~0,47.
Le puits canadien permet d'économiser 47 % de l'énergie utile à
chauffer l'air renouvellé.
La maison est chauffée grâce à
une chaudière
aux granulés de bois. Le kWh est facturé à un
prix de 0,063 €.
Une publicité annonce :
« Le puits
canadien permet d’économiser environ 236 €, au cours d’une période de
six mois
de chauffage ».
4) Justifier cette affirmation.
Energie consommée en 6 mois (182 jours ) de chauffage.
Sans puits
canadien : 2,2 108 x182/(3,6 106) =1,1 104
kWh.
Avec puits canadien : (5,9 107 +7,49 107)x182 /
(3,6 106)=6,77 103 kWh.
Economie : 1,1 104-6,77 103 =4,2 103
kWh
4,2 103 x0,063 ~266 €.
5) En
réalité, pour le consommateur, l’économie est moindre Proposer
une explication
La température du sous-sol, à 2 m de profondeur, n'est pas tout à fait
constante au cours de la période de chauffage.
|
|
|
|
Étude
du système d’insufflation d’air
(B)
Mécanique des
fluides. Étude
de l’écoulement d’air.
Afin d’insuffler, dans la maison, l’air
issu
du puits canadien, un ventilateur est placé à la sortie de la
canalisation
principale.
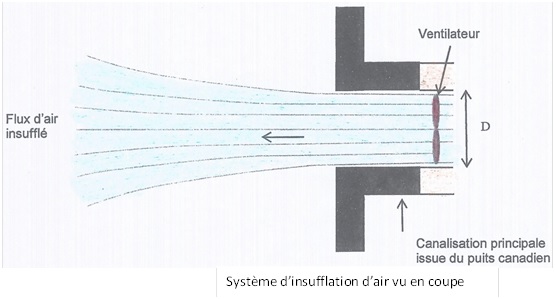
Données :
- Diamètre intérieur de la
canalisation : D = 20,0 cm
- Débit volumique : dv = 83,3.10-3
m3.s-1.
1) Le débit volumique permet-il de
renouveler
entièrement le volume d’air de 300 m3 de la maison en une
heure ?
83,3 10-3 x3600 =299,88 ~300 m3. L'air de la
maison sera entièrement renouvelé en une heure.
2) La
vitesse préconisée pour la circulation
de l’air dans la canalisation ne doit pas excéder 3 m.s-1
afin de
limiter les nuisances sonores du système de ventilation. Cette
contrainte est-elle
respectée ?
Section de la canalisation : S = 3,14 x0,12 = 3,14 10-2
m2.
Vitesse de l'air = dv / S = 83,3 10-3 /(3,14 10-2)=2,65
~2,7 m s-1.
Cette valeur étant inférieure à 3 m /s, les nuisances sonores du
système de ventillation sont limitées.
Acoustique
Étude acoustique du système de
ventilation.
Données : :Seuil d’audibilité de l’oreille
humaine à 1000 Hz : I0
= 1,00.10-12 W.m-2
- La réglementation limite le niveau sonore (niveau d’intensité sonore)
généré par le système d’insufflation d’air à 30 dB(A).
Tableau de pondération.
Fréquence
centrale de la bande d'octave ( Hz)
|
125
|
250
|
500
|
Pondération
(dB)
|
-16
|
-8
|
-3
|
Résultats
des mesures des niveaux d’intensité sonore, par bande
d’octave :
Fréquence
centrale de la bande d'octave ( Hz)
|
125
|
250
|
500
|
Niveau
d'intensité sonore (dB)
|
30
|
30
|
30
|
Le
ventilateur du système
d’insufflation d’air émet un bruit dans la pièce où il est installé.
1)
Déterminer les fréquences minimale fmin et maximale fmax
de la bande d’octave centrée sur la fréquence 250 Hz.
fmin = 250 / 2½ = 250 / 1,414 ~177 Hz.
fmax = 250 x 2½ = 250 x 1,414 ~354 Hz.
On désire savoir si le système
d’insufflation
d’air est conforme à la réglementation acoustique
2) Pour
cela, calculer le niveau d’intensité sonore pondéré pour chacune
de ces bandes, puis le niveau sonore global (dB
(A)).
Le
système d’insufflation d’air est-il
conforme à la réglementation ?
Fréquence
centrale de la bande d'octave ( Hz)
|
125
|
250
|
500
|
Niveau
pondéré (dB) N
|
30-16
=14
|
30-8=22
|
30-3=27
|
Intensité
acoustique ( W m-2) = 10-12 x 100,1N
|
10-12
x101,4 ~2,5 10-11
|
10-12
x102,2 ~1,6 10-10 |
10-12
x102,7 ~5,0 10-10 |
Itotal
= 2,5 10-11 +1,6 10-10 +5,0 10-10
~6,9 10-10 Wm-2.
N = 10 log(6,9 10-10 / 10-12)~28 dB(A).
Cette valeur étant inférieure à 30 dB(A), la réglementation est
respectée.
|
|
|
|
Chimie organique
1- Choix du matériau constituant les
tuyaux.
Il existe plusieurs possibilités quant au
choix du matériau constituant le tuyau enterré à travers lequel s’effectuent
les échanges thermiques.
Il est courant d’utiliser des matières
plastiques comme le polyéthylène (PE) ou le polychlorure de vinyle (PVC).
Ces matières plastiques sont essentiellement
constituées de polymères.-[-CH2-CHCl-]-n.
1) Qu’est-ce qu’un polymère ?
Macromolécule
obtenue ą partir d'un grand nombre de petites molécules (
monomčre) , associées par liaisons de covalence.
2) Que représente le degré de polymérisation n qui apparait dans la formule
du PVC ?
n représente le nombre d'unités de monomères constituant le polymère.
3) Écrire la formule développée de la molécule à partir de laquelle le
PVC est synthétisé.
4) Écrire l’équation modélisant la réaction de synthèse du PVC.
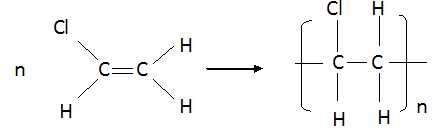
2- Chauffage par combustion.
Le puits canadien
n’étant pas suffisant pour apporter toute l’énergie nécessaire durant la
période hivernale, la maison est équipée d’une chaudière à bois fonctionnant
avec des granulés de bois.
Données :
- Masse volumique des granulés de bois : ρ = 650 kg.m-3
- Pouvoir calorifique des granulés de bois : PC = 4,90 kWh.kg-1
- Volume molaire des gaz : 24,0 L.mol-1
- Énergie fournie par la chaudière pour six mois de chauffage : E
= 6,80.103 kWh
- Le bois est constitué principalement de cellulose, polymère du glucose,
de formule : (C6H10O5)n
- En volume, l’air est composé d’environ 20% de dioxygène.
1) Recopier et
ajuster l’équation de la réaction de combustion complète d’un motif élémentaire
C6H10O5 de cellulose réagissant avec le
dioxygène de l’air.
C6H10O5 + 6O2 ---> 6 CO2 + 5H2O.
2) Sachant que la
chaudière a un rendement de 90%, montrer que la masse de granulés de bois,
nécessaire pour la période de chauffage, est égale à 1,54 t.
Avec un rendement de 100% : 6,80 103 / 4,90=1388 kg.
Avec un rendement de 90% : 1388 / 0,9 ~1,54 103 kg =1,54 t.
3) En déduire le
volume de granulés de bois nécessaire pour la période de chauffage.
1,54 103 / 650=2,37 m3.
4) Calculer la masse
molaire du motif élémentaire de cellulose, C6H10O5.
M = 6 x12 +10 +5 x16=162 g / mol.
5) En déduire la
quantité, exprimée en mol, de motifs élémentaires C6H10O5
consommée durant la période de chauffage.
n = 1,54 106 / 162 =9506 ~9,51 103 mol.
6) Déterminer le
volume de dioxygène consommé lors de la période de chauffage.
6 n=6 x 9506 ~5,70 104 mol.
5,70 104 x 24 = 1,37 106 L = 1,37 103 m3.
7) En déduire le
volume d’air nécessaire.
5 x1,37 103=6,84 103 m3.
L’air est renouvelé
avec un débit constant de 300 m3.h-1.
8) Ce débit est-il
suffisant pour assurer une combustion complète du bois pendant les six mois de
chauffage ?
6 mois = 6 x180 x24=2,59 104 heures.
Débit minimal pour assurer une combustion complète. 6,84 103 / (2,59 104) = 0,26 m3 / h.
Un débit constant de 300 m3.h-1 est largement suffisant.
|
|

