Diffraction par une poudre de cacao. bac S Amérique du Nord 2017. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . On attribue la découverte de la diffraction à Francesco Grimaldi (1618-1663). Le but de l’exercice est d’étudier une application pratique de la diffraction : la détermination de la taille moyenne de poudre de cacao par granulométrie. Granulométrie laser de la poudre de cacao. L’appareil  permet de mesurer la taille de particules allant de 40 nm à 2500 μm tout en occupant un encombrement extrêmement réduit. Le fabriquant de l’appareil indique que deux diodes laser de longueurs d’onde 635 nm et 830 nm sont utilisées dans cet instrument de mesure. Différents types de chocolat. Le succès du chocolat, auprès des consommateurs, est lié à des caractéristiques gustatives bien identifiées mais aussi à la granulométrie de chacun des constituants. Cette dernière propriété représente un enjeu important du procédé de fabrication puisque des particules trop finement broyées rendront le chocolat collant alors que de trop grosses particules lui donneront un aspect granuleux à l’oeil et en bouche. La mesure de la taille des particules, par diffraction laser, est une technique simple et rapide, adaptée à la détermination de la distribution granulométrique de tous les types de chocolat comme les chocolats de couverture utilisés pour le nappage, les chocolats au lait ou les chocolats agglomérés utilisés pour lesrecettes instantanées. Type de chocolat De couverture Au lait Aggloméré Diamètre moyen recommandé a en µm 10 30 300 D’après http://www.es-france.com/pdf/010-Cacao.pdf Partie 1 : Vérification de la longueur d’onde d’une des diodes laser utilisées. L’objectif de cette partie est de vérifier la valeur de la longueur d’onde l d’une des diodes laser utilisées dans l’appareil de granulométrie. Sur le trajet du faisceau laser, on intercale des fils de différents diamètres. Sur un écran placé à une distance D, on observe une figure de diffraction. L représente la largeur de la tache centrale et θ le demi-angle au sommet exprimé en radian. 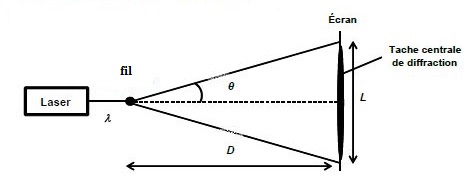D = 200±0,1 cm. 1.1. Rappeler les trois principales propriétés du faisceau d’un laser. La lumière laser est monochromatique. Le faisceau est très directif. La puissance par unité de surface est très grande. La lumière laser est cohérente. 1.2. Pour une longueur d’onde donnée, décrire l’évolution du demi-angle θ en fonction du diamètre a du fil. Donner la relation qui lie λ, θ et a. q = l / a. Pour une longueur d'onde donnée, q et a sont inversement proportionnels. Lorsque a croît, l'angle q diminue. 1.3. On fait l’hypothèse que l’angle θ est petit. Dans ce cas, on peut écrire tan θ ≈ θ avec θ en radian. À l’aide du schéma, démontrer que la largeur de la tache centrale est donnée par l’expression: L = k .1 /a avec k = 2 λ D. D'autre part, pour les petits angles : tan q ~q ( radian) ~½L / D. Par suite : ½L / D= l / a ; L = 2 λ D / a. 1.4. Expérimentalement, on mesure la largeur de la tache centrale L pour des fils calibrés de différentes valeurs de diamètre a. On porte les valeurs obtenues sur le graphique ci-dessous. Dk / k)2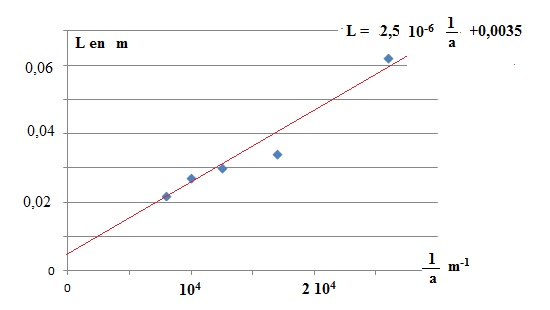 L’incertitude absolue sur la valeur du coefficient directeur est Δk = 1,2 × 10–7 m2 . Exprimer la valeur de la longueur d’onde λ avec son incertitude. Confronter aux valeurs données par le fabriquant de l’appareil ; conclure. l = k / (2D ) =2,5 10-6 / (2*2,00) = 6,25 10-7 m = 625 nm. Dl / l= [(Dk / k)2+(DD / D)2]½=[(1,2 10-7 /(2,5 10-6))2 +(0,1 / 200)2]½ =4,8 10-2. Dl =4,8 10-2 x625 ~30 nm. l = 625 ±30 nm. l appartient à [595 ; 655 nm] ; la valeur indiquée par le fafricant appartient à cet intervalle. Les valeurs sont valides. .............. ................. Partie 2 : Étude de la diffraction par la poudre de cacao Dans cette partie, on considère que l’on peut déterminer le diamètre moyen des grains de cacao d’une poudre donnée en utilisant une figure de diffraction réalisée avec la diode laser de longueur d’onde λ = 635 nm. La figure de diffraction obtenue par un trou circulaire est constituée de cercles concentriques alternativement brillants et sombres avec : sin θ=1,22 λ /a λ : longueur d’onde du faisceau laser, exprimée en mètre a : diamètre du trou, exprimé en mètre θ : demi-angle au sommet, exprimé en radian 2.1. En utilisant un montage proche de celui donné ci-dessus, on réalise l’expérience sur un échantillon de poudre de cacao. Sachant que les grains de cacao sont assimilés à des sphères, justifier le fait qu’on observe une figure de diffraction identique à celle obtenue avec un trou circulaire. Le grain circulaire est un obstacle pour la lumière laser ; il se comporte comme un trou circulaire et donne la même figure de diffraction. 2.2. Après traitement informatique des résultats expérimentaux lors du contrôle d’un échantillon de poudre de cacao, on obtient le graphe ci-dessous donnant l’intensité lumineuse relative sur l’écran en fonction du demi-angle θ. Peut-on utiliser cet échantillon pour un chocolat de couverture ? 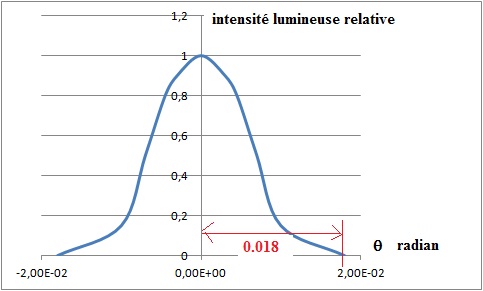a =1,22 l / sin q = 1,22 x635 10-9 / sin 0,018 =4,3 10-5 m = 43 µm. Ce grain est trop gros pour un chocolat de couverture. .

menu