Bâtiment à énergie
positive,
bac
STi2d Stl Antilles 09/ 2017 .
|
|
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
|
|
|
|
Partie
A – Le solaire.
A.1 Le solaire thermique.
On s’intéresse dans cette partie à la production d’eau chaude par un
panneau solaire thermique.
A.1.1 Description
du panneau thermique
Simplement décrit, un panneau solaire thermique est une boîte noire
mate isolée, coiffée d’une vitre. À l’intérieur se trouve un serpentin
de même couleur à travers lequel circule un fluide caloporteur avec un
débit modulable. Le rayonnement solaire absorbé par le panneau chauffe
le liquide caloporteur.
A.1.1.a Expliquer
pourquoi le corps du panneau est noir mat.
L'absorbeur de couleur sombre possède un coefficient d'absorption élevé
et un coefficient d'émission faible.
A.1.1.b Justifier
la nécessité de la vitre transparente. Préciser la nature du
rayonnement piégé par l’absorbeur.
Le vitrage doit laisser passer la lumière solaire. Le rayonnement
infrarouge se trouve piègé.
A.1.1.c Quel est
l’intérêt d’un circuit en serpentin pour le fluide caloporteur ?
La surface de contact entre le fluide caloporteur et le rayonnement
infrarouge est plus important.
A.1.2
Fonctionnement du panneau thermique
Dans les conditions d’étude, la puissance solaire surfacique reçue au
niveau du sol est de 800 W m -2.
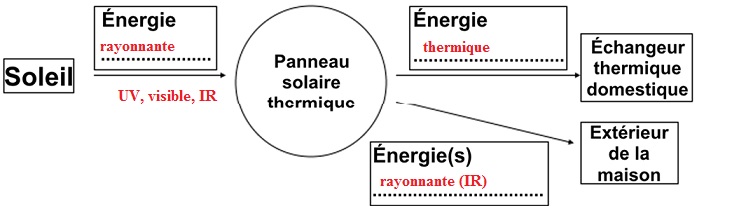
A.1.2.a Compléter
le schéma du diagramme énergétique du panneau solaire thermique.
 A.1.2.b
A.1.2.b Dans une
première approche théorique, on suppose que le fond noir du panneau
absorbe toute la puissance solaire reçue au niveau du sol, puis qu’il
la restitue. Que vaut alors la valeur de cette puissance surfacique,
notée P fond ?
P fond = 800 W m -2.
A.1.2.c En
supposant que le fond rayonne en respectant la loi de Stefan, calculer
la température théorique, T théorique, du fond du panneau, en
kelvins puis en degrés Celsius.
P fond = 5,67 10 -8 T 4théorique.
T théorique = (P fond / (5,67 10 -8)) 1/4
= (800 / (5,67 10 -8)) 1/4 ~345 K ou 345-273 =72°C.
A.1.2.d En réalité,
le fluide caloporteur est à l’équilibre thermique à 50°C. Critiquer la
démarche théorique posée ci-dessus.
Une partie de l'énergie solaire reçue est rémise vers l'extérieur sous
forme de rayonnement IR.
|
....
.....
|
A.2 Le
solaire photovoltaïque.
Dans cette partie, on s’intéresse à la production d’électricité par
l’effet photovoltaïque puis on cherche à vérifier la cohérence d’un
chiffre publié par la société ABALONE énergie.
A.2.1 Conversion
énergie rayonnante / énergie électrique
Pour que la cellule photovoltaïque présente dans le panneau produise un
courant, la valeur minimale d’énergie apportée par les photons doit
être Emini = 1,12 eV.
A.2.1.a Montrer que
la fréquence minimale pour laquelle la cellule permet le passage du
courant est nmini
= 2,70 1014 Hz.
nmini = Emini / h = 1,12 x1,6 10-19
/(6,63 10-34) =2,70 1014 Hz.
A.2.1.b En déduire
la longueur d’onde maximale, lmax,
correspondante exprimée en µm.
lmax
= c / nmin
=3,00 108 /(2,70 1014)= 1,11 10-6 m =
1,11 µm.
A.2.1.c Rappeler
les limites du domaine du visible et en déduire dans quel domaine des
ondes électromagnétiques se situe ce rayonnement.
Limites du visible : 400 µm - 800 µm.
Le rayonnement précédent appartient au proche infrarouge.
A.2.2
Caractéristiques des panneaux photovoltaïques
Déterminer la valeur manquante du tableau.
Puissance
nominale maximale
|
Pnom
|
236
W
|
Tension
à puissance nominale
|
Vpm
|
50,4
V
|
Courant
à puissance nominale
|
Ipm
|
Pnom
/ Vpm = 236 / 50,4 ~4,68 A
|
A.2.3 Utilisation des panneaux
La puissance solaire surfacique reçue au niveau du sol est toujours ici
de 800 W m-2. La surface d’un panneau est d’environ 1,5 m2.
A.2.3.a Calculer la
puissance solaire, Pp, reçue par un panneau.
Pp = 800 x1,5 = 1,2 103 W.
A.2.3.b Définir
puis calculer le rendement, h,
d’un panneau.
h = Pnom
/ Pp = 236 / 1200 =19,7 ~20 %.
La surface totale des panneaux est 80 m2.
A.2.3.c Dans les
conditions d’utilisation des panneaux, montrer que la puissance
électrique totale produite par l’installation est d’environ Ptot
= 13 kW.
Nombre de panneaux : 80 / 1,5 ~53.
Ptot = Pnom x 53 = 236 x53 ~1,25 104 W
~13 kW.
La durée annuelle d’ensoleillement, pour les conditions évoquées, de la
région de construction du bâtiment est d’environ Dt = 1900 h. On négligera
les autres situations d’ensoleillement.
A.2.3.d Calculer,
en MWh, l’énergie électrique, Etot, que fournira
l’installation photovoltaïque par an.
Etot = 13 x1900 =2,47 104 kWh ~ 25 MWh.
La société annonce 20 MWh par an.
A.2.3.e Est-ce en
accord avec la valeur calculée ? Proposer une explication.
Les panneaux ne fonctionnent pas toujours dans les conditions optimales
; la puissance peut être inférieure à la puissance nominale. La valeur
annoncée par la société est en accord avec les calculs.
..
|
|
|
Partie
B : L'éolien.
Dans cette partie, on s’intéresse à la production d’électricité par une
éolienne puis on cherche à vérifier la
cohérence d’un chiffre publié par la société ABALONE énergie.
B.1 L’énergie du
vent
Une éolienne a pour but de transformer l’énergie du vent en énergie
électrique. Elle est constituée d’une hélice qui entraine un arbre lié
à un générateur. Ce dernier produit l’énergie électrique.
Avant l’éolienne, le vent a une vitesse, v1, plus grande que
sa vitesse, v2, après l’éolienne.
B.1.1 Comment
appelle-t-on l’énergie liée à un corps en mouvement ?
Energie cinétique.
Pendant une durée Dt,
un volume d’air, Vair, compris dans le cylindre de base S et
de longueur L vient frapper l’éolienne.
B.1.2 Exprimer L en
fonction de la vitesse, v, du vent et de la durée, Dt.
Vair = SL avec L = v Dt.;
B.1.3 Exprimer
alors le volume d’air, Vair, en fonction de v, Dt et S.
Vair = v S Dt.
B.1.4 En utilisant
la masse volumique de l’air, rair,
exprimer la masse d’air, m, qui frappe l’éolienne pendant Dt.
m = rair
Vair = rair
v S Dt.
B.1.5 Après avoir
rappelé l’expression de l’énergie cinétique de translation d’un corps
de masse, m, et de vitesse, v, montrer que l’énergie cinétique, Ec,
du vent captée par l’éolienne pendant la durée, Dt, s’exprime comme : Ecvent
= ½rair
Dt S v3.
Ec = ½mv2 ; Ecvent = ½ rair
v S Dt.v2= ½rair
Dt S v3.
B.1.6
Rappeler la relation entre la puissance mécanique, Pcvent,
l’énergie du vent, Ecvent, et la durée, Dt.
En déduire alors que Pcvent = ½rair S v3.
Pcvent = Ecvent / Dt= ½rair
S v3.
B.1.7
Application : la vitesse du vent est v1 = 54 km /h.
Convertir cette vitesse en m s-1
puis montrer que la puissance mécanique du vent, Pcvent1,
vaut, dans ces conditions, Pcvent1 = 42 kW.
Données : S= 20 m2 ; rair=1,23 kg m-3 dans ces
conditions.
v = 54 / 3,6 =15 m/s ; Pcvent1
=0,5 x1,23 x20 x153=4,15 104 W ~42 kW.
B.2
L’énergie électrique fournie au réseau
La société Abalone Énergie annonce une puissance électrique générée par
éolienne
Pthéorique = 10 kW.
B.2.1 Compléter le
diagramme énergétique éolienne.
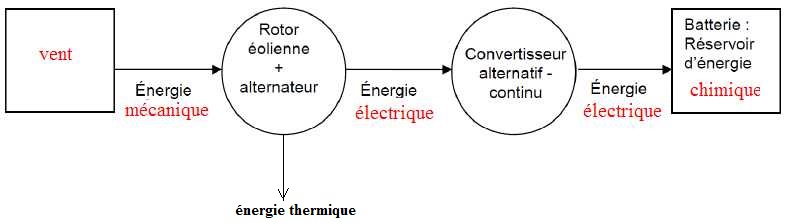
L’allemand Albert Betz en 1919 a montré que la part de puissance
cinétique maximale qui peut être extraite du vent et fournie à
l’éolienne est limitée. En pratique la puissance extraite du vent, Pcextraite,
peut être calculée par la formule suivante :
Pcextraite ≈ 0,44× Pcvent.
Le rendement de la chaine énergétique de l’éolienne est h ≈ 89 %.
B.2.2 Montrer que
la puissance électrique générée par l’éolienne est Pél1 = 16
kW.
Pél1 =0,44 x0,89 Pcvent1 =0,44 x0,89 x42 ~16 kW.
B.2.3 Comparer les
puissances calculée et indiquée par l’entreprise, en calculant l’écart
relatif à la valeur indiquée. Commenter.
(16-10) / 16 ~0,38. (38 %)
La vitesse du vent n'est pas constante, mais irrégulière. La puissance
électrique réelle est inférieure à la puissance maximale.
|
|
|
|
Partie C. La protection du matériel.
Dans
l’éolienne, les différents éléments métalliques constitutifs sont
exposés à l’air ambiant qui peut être salin. Il faut donc les protéger
de la corrosion. Pour protéger une pièce d’aluminium, on la recouvre
par électrolyse, d’une couche d’alumine
(Al2O3(s)) isolante de quelques micromètres
d’épaisseur.
Lors de l’électrolyse, la pièce en aluminium joue le rôle d’anode et
une plaque de plomb celui de la cathode. Les deux sont plongées dans un
bain d’acide sulfurique (2H+ + SO42-)
concentré. Voici les demi-équations des réactions qui ont lieu aux
électrodes :
• anode : 2 Al(s) +3H2O(l) = Al2O3(s)
+6H+aq + 6e-.
• cathode : 2H+aq +2e- = H2(g).
Un générateur de tension fournit un courant d’intensité I=250 A.
C.3.1 Compléter le
schéma du montage, suivant les consignes qui y sont indiquées.
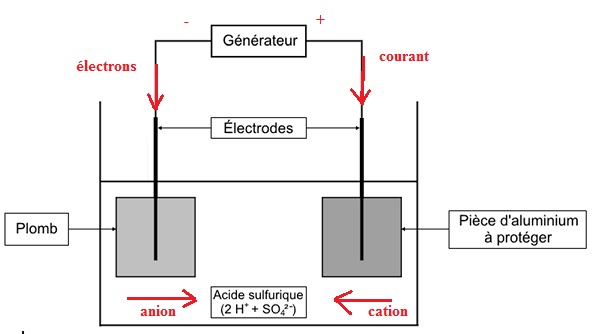
C.3.2 Écrire
l’équation bilan de cette électrolyse.
2 Al(s) +3H2O(l) +6H+aq +6e- = Al2O3(s)
+6H+aq + 6e-+3H2(g).
2 Al(s) +3H2O(l) = Al2O3(s)+3H2(g).
C.3.3 Une couche
d’alumine d’épaisseur 14,8 µm et de surface totale S = 0,872 m2
se forme sur la pièce à protéger.
Données :
Valeur absolue de la charge d’une mole d’électrons ou constante de
Faraday : F = 9,65 104 C mol-1.
Masse volumique de l’alumine : r
= 3,95 106 g m-3.
Masse molaire de l’alumine : MA = 102 g / mol
C.3.3.a Calculer le
volume, Va, puis la masse, ma, de la couche
d’alumine.
Va = 14,8 10-6 x0,872 =1,29 10-5 m3.
ma = 1,29 10-5 x3,95 106 ~51 g.
C.3.3.b Montrer
alors que la quantité de matière d’alumine formée est nA=
0,500 mol.
ma / Ma = 51 / 102 = 0,50 mol..
C.3.4 À partir de
la demi-équation à l’anode, calculer la quantité d’électrons mise en
jeu pour 0,500 mol d’alumine formée et en déduire que la charge
électrique (en coulomb) mise en jeu lors de l’électrolyse est de 2,89 105
C.
6 x0,50 = 3,0 mol d'électrons soit 3,0 x9,65 104 =
2,89 105 C.
C.3.5 À l’aide de
l’intensité du courant électrique, calculer la durée de cette
anodisation.
2,89 105 / 250 =1,16 103 s.
|
Partie D. Stockage de l'énergie.
Nous cherchons dans cette partie à vérifier la cohérence du document
d’introduction ;
c’est-à-dire utiliser l’énergie électrique générée la nuit par les 3
éoliennes de 10 kW chacune pour produire par électrolyse du
dihydrogène, le stocker sous forme gazeuse puis utiliser une
pile à combustible pour restituer de l’énergie sous forme électrique le
moment voulu.
D’après le site : http://www.ehd2020.com/ pour produire 1,0 kg
d’hydrogène, il faut 75 L d’eau et environ 70 kWh d’électricité.
Par ailleurs, 1,0 kg d’hydrogène contient 33 kWh d’énergie au maximum.
D.1 Voici les deux
pictogrammes que l’on trouve sur une bouteille de dihydrogène. Rappeler
leurs significations.

D.2 Montrer que
l’énergie que peuvent fournir la nuit (12 h) l’ensemble des éoliennes
sur un an est Wel = 1,3 105 kWh.
30 x 12 x365 = 1,3 105 kWh.
D.3
Calculer alors la masse de dihydrogène qui peut être produite par
électrolyse.
1,3 105 / 70 = 1,877 103 ~1,9 103 kg.
D.4 Montrer alors
que l’énergie maximum disponible dans le dihydrogène est WH2
= 6,2 104 kWh.
1,9 103 x33 ~ 6,2 104 kWh.
Pour
stocker le gaz, il faut dépenser 15 % de l’énergie précédente, et, pour
obtenir de l’énergie électrique via une PAC basse température (100 à
200°C), le rendement est de l’ordre de 45 %.
D.5 Montrer alors
que l’énergie électrique potentiellement restituée est largement
supérieure aux 7500 kWh sur un an mentionnés dans le texte
d’introduction.
Energie nécessaire au stockage : 6,2 104 x0,15 = 9,3 103
kWh.
Energie restante : 6,2 104 -9,3 103 = 5,3 104
kWh.
Energie restituée : 5,3 104 x 0,45 ~2,4 104 kWh,
environ 3 fois supérieure à 7500 kWh.
|
|