L'avion solaire
Solar Impulse 2,
bac
STLB Antilles 2017 .
|
|
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
|
|
|
|
Partie A : la mécanique du vol d’un avion
et la course au poids pour Solar Impulse 2.
A.1. Forces
exercées sur un avion en vol
A.1.1. Identifier
chacune des quatre forces en les mettant en correspondance avec les
définitions.
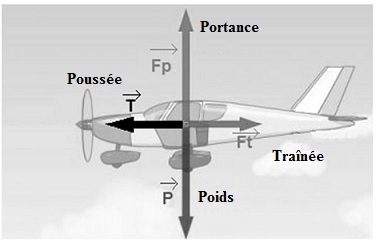 A.1.2
A.1.2. Préciser, en
justifiant, quelle force parmi les quatre identifiées permet à l’avion
d’être
maintenu en l’air.
La seule force dirigée vers le haut est la portance FP.
A.1.3. Indiquer, en
justifiant, quelle est la force dont la valeur ne varie pas lors du vol.
Le poids, P=mg, ne dépend pas
de la vitesse de l'avion.
A.1.4. En
s’appuyant sur les caractéristiques techniques de l’avion , calculer
son poids.
Masse de l'avion m = 2300 kg ; p = mg = 2300 x9,81 ~ 2,26 104 N.
A.1.5. Expliquer
comment varie la portance quand la vitesse de l’avion augmente.
F P =0,5.ρ.S.C z.v 2
(ρ : masse volumique de l'air en kg m –3 ; S : surface des
ailes en m 2 ; v : vitesse de
déplacement en m.s -1 ; C z : coefficient de
portance sans unité).
La portance est proportionnelle au carré de la vitesse.
A.1.6. Dire quelle
condition doit remplir la force de portance pour que l’avion décolle.
La portance doit être supérieure au poids.
A.2. Vitesse de
décrochage
A.2.1. En prenant C z
= 1,5 et une surface des ailes S = 250 m², montrer que la vitesse que
Solar Impulse 2 doit atteindre pour remplir la condition précédente est
de 36 km.h –1. Cette
vitesse est appelée vitesse de décrochage.
Donnée :
La masse volumique de l’air au niveau du sol est r = 1,2 kg.m –3..
FP =0,5.ρ.S.Cz.v2 > mg. v2 > mg / (0,5.ρ.S.Cz).
v2> 2,26
104 /(0,5 x1,2x1,5x250) ; v2 > 102 ; v > 10 m s-1
soit 36 km h-1.
A.2.2.
En réalité, à cause des frottements des roues du train d’atterrissage,
il faut atteindre
1,3 fois la vitesse de décrochage pour décoller sans risque. Déterminer
la valeur de la
vitesse de décollage et montrer qu’elle est conforme aux données. Sa
vitesse de décollage est de 47 km.h –1.
36 x1,3 ~47 km h -1.
A.2.3. En utilisant
le graphe, déterminer la masse volumique de l’air à 9000 m d’altitude.
Proposer une interprétation simple de la diminution de la masse
volumique avec l’altitude.
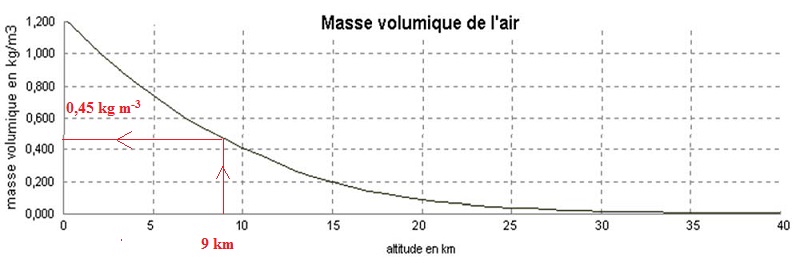
La pression de l'air diminue avec l'altitude.
A.2.4. En utilisant
le constat précédent et l’expression de la portance , montrer que la
vitesse de décrochage est plus grande à 9000 m d’altitude qu’au niveau
du sol.
v2
> mg / (0,5.ρ.S.Cz) ;
v2> 2,26 104
/(0,5 x0,45x1,5x250) ; v2 > 2,68 102 ;
v > 16,36 m s-1
soit 59 km h-1.
|
....
.....
|
A.3. La course au poids
A.3.1. Expliquer
pourquoi le poids joue un rôle crucial, surtout de nuit, lorsque Solar
Impulse 2 ne peut utiliser que l'énergie électrique de ses batteries.
Plus le poids est grand, plus la portance doit être élevée. Donc
la vitesse doit être plus élevée pour éviter le décrochage. Plus la
vitesse est grande, plus l'énergie consommée est grande. La nuit les
batteries fournissent l'énergie nécessaire.
A.3.2. La masse
volumique du silicium est de 2330 kg.m–3. En déduire la
masse des 269,5 m2 de cellules solaires photovoltaïques dont
l’épaisseur est de 135 µm. Rappel : 1 micron = 1μm = 10 –6 m.
Volume de silicium : V = 269,5 x135 10-6 = 3,63825 10-2
m3.
Masse correspondante : 3,63825 10-2 x2330 ~84,8 kg.
A.3.3. Les
batteries représentent une part importante de la masse de l’avion.
Masse des batteries : 633 kg.
Calculer le pourcentage de la masse totale de l’avion qu’elles
représentent
633 / 2300 x100 ~27,5 %.
A.3.4. La structure
de Solar Impulse 2 est réalisée en matériau composite constitué d’une
peau en résine et fibres
de carbone, dont la masse par unité de surface est inférieure à 25 g.m-2.
Préciser ce qu’est un matériau composite.
Assemblage d'au moins deux matériaux non miscibles dont les propriétés
se complètent.
Partie B : le challenge
énergétique à relever.
B.1. La puissance
des moteurs
B.1.1. Montrer que
la puissance maximale développée par les quatre moteurs fonctionnant
ensemble est de 51,5 kW.
Quatre moteurs brushless sensorless de 17,5 ch. 1 ch = 735,5 W.
4 x17,5 x735,5 =5,15 104 W = 51,5 kW.
Le diagramme d’énergie d’un moteur électrique est le suivant :
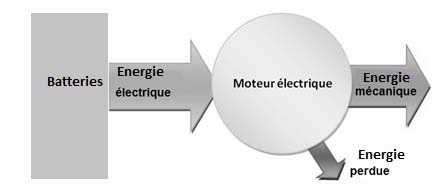
B.1.2. Compte tenu
du rendement du moteur ( 94 %), montrer que la puissance
électrique absorbée par les quatre moteurs fonctionnant à pleine
puissance est de 54,8 kW.
51,5 / 0,94 =54,8 kW
B.2. L’énergie
stockée dans les batteries
B.2.1. Déterminer
en kW.h l’énergie maximale pouvant être stockée dans les batteries de
l’avion.
Batteries au lithium polymère, d’une densité énergétique de 260 W.h.kg–1.
633 x 260 =1,6458 105 W ~165
kW.
B.2.2. En admettant
que les quatre moteurs fonctionnent à pleine puissance, montrer que la
durée maximale d’utilisation des batteries serait alors de 3,0 heures.
165 / 54,8 ~3,0 heures.
|
|
|
B.3.
Le vol de jour
Le jour, l’avion est soumis à une puissance solaire surfacique moyenne
de 1000 W.m-2.
B.3.1. Calculer, en
kW, la puissance solaire reçue par les 269,5 m2 de cellules
solaires de l’avion.
269,5 x1000 =2,695 105 W ~269
kW.
B.3.2. Le diagramme
des puissances d’une cellule solaire est le suivant :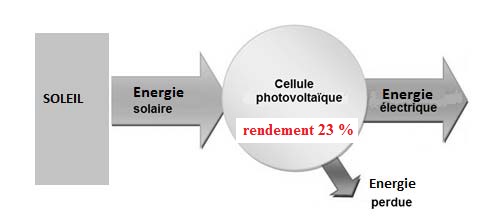
En tenant compte du rendement de 23 % des cellules solaires, montrer
que la puissance électrique que peuvent fournir les cellules solaires
de l’avion est de 62,0 kW.
269 x0,23 ~62,0 kW.
B.3.3. En
justifiant la réponse, indiquer si cette puissance est suffisante pour
alimenter les quatre moteurs fonctionnant à pleine puissance.
Oui, 62 est supérieur à 54,8, puissance électrique maximale absorbée
par les moteurs.
B.3.4. En admettant
que 25 % de la puissance électrique produite par les cellules solaires
est en moyenne utilisée pour la recharge des batteries, calculer la
durée d’exposition solaire nécessaire pour recharger intégralement les
batteries de l’avion.
Puissance reçue par les batteries : 62,0 x0,25 =15,5 kW.
Durée de la recharge : 165 / 15,5 ~10,6 h.
B.3.5. Quel type
d’énergie est utilisé pour la propulsion de l’avion durant le vol de
jour ?
Energie solaire.
B.3.6. Compléter le
diagramme en énergie de l’avion solaire volant de jour.
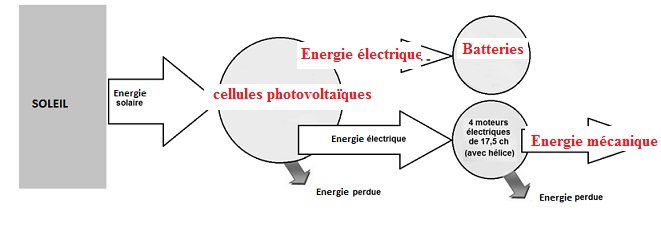
|
|
|
|
B.4.
Le vol de nuit
B.4.1. Indiquer la
forme d’énergie utilisée pour la propulsion de l’avion en début de nuit
(après 21 h 30) puis en fin de nuit.
L'énergie potentielle de pesanteur est utilisée en début de nuit ; en
fin de nuit l'avion utilise l'énergie électrique fournie par les
batteries.
B.4.2. En admettant
qu’à 7 heures du matin l’avion reprend les conditions énergétiques du
vol de jour, calculer la durée pendant laquelle les batteries doivent
assurer l’alimentation des moteurs.
" à 21h30, son pilote éteignait le générateur solaire. Pendant quatre
heures, l’avion a volé sans apport d’électricité, uniquement en se
laissant descendre".
21 h 30 + 4 =1 h 30 le lendemain.
7 h -1h 30 = 5 h 30 min.
B.4.3.
Compte tenu du résultat précédent et de celui de la question B.2.2.,
expliquer pourquoi l’avion ne peut pas adopter une vitesse maximale
durant cette phase de vol à 1500 m d’altitude.
A vitesse maximale, les batteries sont déchargées au bout de 3 heures.
Il doit donc voler à vitesse minimale.
B.4.4. Compléter le
diagramme en énergie de l’avion solaire volant de nuit.
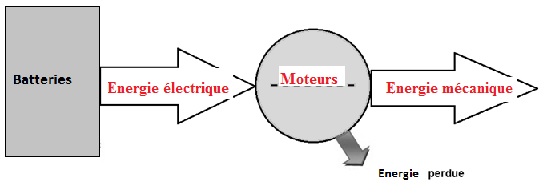
Partie C : les cellules
photovoltaïques à haut rendement
C.1. Le rayonnement
solaire
C.1.1. À l’aide du
spectre du rayonnement solaire, quelle(s) espèce(s) chimique(s)
est(sont) la cause d’une partie de l’absorption du rayonnement
solaire constatée au niveau de la mer pour le rayonnement UV, puis pour
le rayonnement infrarouge ?
L'ozone absorbe en partie les UV.
Le dioxyde de carbone et l'eau absorbent en partie l'infrarouge.
C.1.2. Quel risque
représente le rayonnement UV pour l’homme ?
Cataracte, cancer.
C.1.3. En le
justifiant, dire si le danger est plus important à basse ou à haute
altitude.
En haute altitude les UV sont moins absorbés. Le danher est plus
important.
C.2. Le choix des
cellules photovoltaïques
On donne quelques caractéristiques de trois types de cellules
photovoltaïques existantes :
Type
de matériaux de la cellule
|
Durabilité
|
Rendement
typique en %
|
Rendement
maximum en %
|
Coût
de fabrication
|
Silicium
monocristallin
|
>
20 ans
|
15
à 20
|
25
|
+++
|
Silicium
polycristallin
|
>
20 ans
|
12
à 16
|
20
|
++
|
Silicium
amorphe
|
20
ans
|
5
à 8
|
13
|
+
|
C.2.1. Expliquer
pourquoi les concepteurs de l’avion Solar Impulse 2 ont retenu les
cellules en silicium monocristallin.
Le rendement est bien supérieur au silicium polycristallin et au
silicium amorphe.
C.2.2. Le rendement
de 23 % des cellules photovoltaïques de Solar Impulse 2 est l’un des
meilleurs rencontrés pour ce type de convertisseur d’énergie à l’heure
actuelle. Ce rendement peut-il être qualifié de bon pour un
convertisseur d’énergie ? Justifier la réponse.
Non. Ce rendement est faible par rapport à celui des moteurs
électrtiques.
C.3. L’effet
photoélectrique
Les théories actuelles associent à chaque onde électromagnétique du
rayonnement solaire une particule appelée photon dont l’énergie est
donnée par la relation de Planck :
E = h.n = h. c / λ
Avec : E : énergie du photon (J) ; n : fréquence de l’onde
électromagnétique (Hz) ;
c : célérité de la lumière dans le vide (m.s–1) ; λ :
longueur d’onde de l’onde électromagnétique (m).
Données :
c = 3×108 m.s-1 h = 6,62×10–34 m².kg.s-1
1 eV = 1,6×10 –19 J 1 nm = 1×10 –9 m
Seuls les photons dont l’énergie est supérieure à Eg = 1,12
eV (appelé gap du silicium) peuvent libérer un électron qui participera
au courant électrique délivré par la cellule photovoltaïque en silicium.
C.3.1. Déterminer
en nm la longueur d’onde de l’onde électromagnétique dont le photon a
une énergie égale au gap du silicium. Dans quel domaine d’onde se situe
cette radiation ?
l = hc
/ E avec E =1,12 x1,6 10-19 = 1,792 10-19 J.
l =
6,62 10-34 x3 108 /(1,792 10-19) =1,1 10-6 m. ( Domaine IR).
C.3.2. Indiquer à
quelle(s) zone(s) (A, B ou C) correspondent les photons potentiellement
utiles à la production d’énergie électrique par le silicium ?
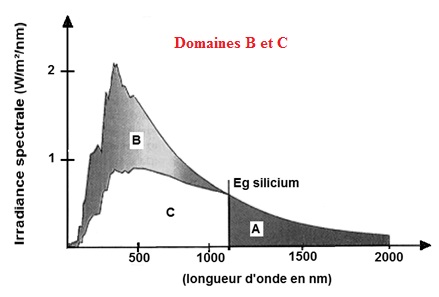
|
Partie D : les
batteries Lipo
D.1. Le choix des batteries
D.1.1. Préciser pourquoi les
batteries au lithium ont un avantage considérable sur les autres batteries pour
le projet Solar Impulse 2.
L'énergie massique est bien plus importante que celle des autres
batteries.
D.1.2. Indiquer les avantages qui
ont vraisemblablement guidé les ingénieurs de Solar Impulse 2 dans le
choix des batteries Lipo plutôt que Li-ion.
Elles peuvent prendre des formes fines et variées.
Leur poids est faible et ell est plus sûre.
Le fonctionnement
d’une batterie Lipo est similaire au fonctionnement d’une batterie
Li-ion.
D.1.3. Indiquer la conséquence de
l’amélioration apportée par les nanotechnologies lors de la recharge de
nos batteries au lithium dans le futur proche.
La recharge des batteries est plus rapide.
D.2. Fonctionnement en générateur
des batteries au lithium
Lors de la décharge d’une
batterie les réactions chimiques intervenant aux électrodes sont modélisées de façon simplifiée par les
équations chimiques ci-après :
- sur l’électrode en
graphite : Li = Li + + e–
- sur l’électrode en
oxyde de cobalt : CoO2 + Li+ + e– =
CoLiO2.
D.2.1. En le justifiant, dire quelle
électrode de la batterie Li-ion est le siège d'une oxydation.
Un oxydation libère des électrons.Le graphite est le siège d'une
oxydation.
D.2.2. Indiquer le sens de
circulation et le nom des porteurs
de charge responsables du passage du courant dans les différentes
parties du circuit ainsi que
les polarités de la batterie lors de son fonctionnement en générateur.
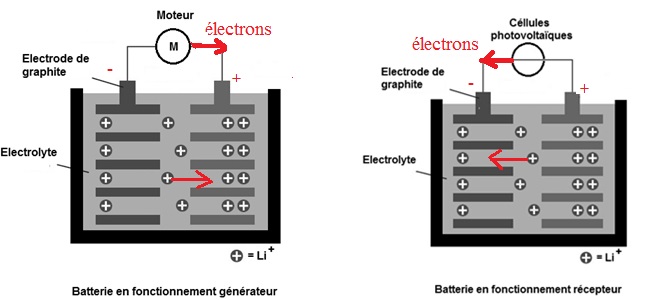
D.3. Fonctionnement en récepteur des
batteries au lithium
D.3.1. Indiquer le sens de
circulation et le nom desporteurs
de charge responsables du passage du courant dans les différentes
parties du circuit ainsi que
les polarités de la batterie lors de son fonctionnement en récepteur.
D.3.2. Écrire les équations
chimiques intervenant aux deux électrodes.
D.3.3. Sur quelle électrode
intervient l’oxydation ?
Oxydation
sur l’électrode en oxyde de cobalt : CoLiO2
= CoO2
+ Li+ + e–
Réduction sur l’électrode
en graphite : Li +
+ e–
= Li.
|
|