Le coeur
artificiel,
bac
STLB métropole 2017 .
|
|
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
|
|
|
|
Partie A : la scintigraphie myocardique
pour diagnostiquer les pathologies du coeur
A.1. Mesure de la F.E.V.G
La scintigraphie myocardique permet principalement
la mesure de
la Fraction d'Éjection Ventriculaire Gauche (FEVG). Elle se définit
comme le rapport entre le volume de sang éjecté et le volume
télédiastolique du ventricule gauche.
A.1.1. La FEVG est
définie ci-après :
FEVG = volume du sang éjecté / volume télédiastolique du ventricule
gauche.
Quelle est l’unité de la FEVG ? Justifier.
En divisant un volume par un volume, exprimés dans la même unité, on
obtient un résultat sans unité.
A.1.2. On réalise
une scintigraphie myocardique d’un patient pour lequel le volume de
sang éjecté est de 32 mL, et le volume télédiastolique de 125 mL.
A.1.2.1. Calculer
la FEVG.
FEVG = 32 / 125 =0,256 ~ 0,26. (
26 %).
A.1.2.2. Ce
résultat est-il normal ?
26 % étant inférieur à 30 %, cette valeur est sévèrement anormale.
A.2. Étude d’un marqueur radioactif : le thallium 201. 20181Tl.
A.2.1. Donner la
composition (nombre de protons et de neutrons) du noyau radioactif de
thallium 201.
81 protons et
201-81 = 120 neutrons.
A.2.2. Le thallium
201 peut se désintégrer en mercure 201:
A.2.2.1. Réécrire
l’équation ci-dessous en la complétant.
20181Tl
---> 20180Hg
+01e.
A.2.2.2. À quel
type de radioactivité correspond cette désintégration ?
Quel est le nom de la particule émise ?
Emission d'un positon,
radioactivité de type ß+.
A.3 Scintigraphie
au technétium
Une scintigraphie myocardique nécessite l’injection par voie
intraveineuse de technétium d’une activité de 480 MBq pour un patient
de 80 kg.
Pour réaliser cet examen, on peut utiliser une solution « Sestamibi »
d’activité volumique égale à 1 millicurie par millilitre (1 mCi/mL)
Données : le curie (Ci) est une unité de radioactivité. Il correspond à
3,7.1010 becquerels (Bq), ce qui est à peu près l’activité
d’un gramme de radium.
Le curie et le becquerel sont utilisés dans le domaine hospitalier.
A.3.1. Que
représente un becquerel (Bq) ?
Le becquerel correspond à une désintégration par seconde.
A.3.2. Quel volume
de solution « Sestamibi » faut-il injecter à un patient de 80 kg pour
mener à bien cet examen ?
480 106 Bq ou 4,80 108 / (3,7 1010)~1,3
10-2 Ci = 13 mCi.
Il faut injecter 13 mL de
solution « Sestamibi
A.3.3.
L’énergie du rayonnement émis par le technétium est de 141 keV.
Calculer la longueur d’onde du rayon émis. Indiquer de quel type de
rayonnement il s’agit.
E = h c / l ; l = hc /E avec E = 141 103
x1,6 10-19 = 2,256 10-14 J.
l =
6,63 10-34 x3,0 108 / (2,256 10-14)~8,8 10-12 m.

A.3.4. La courbe
ci-dessous donne l'activité du technétium 99-m en fonction du temps.
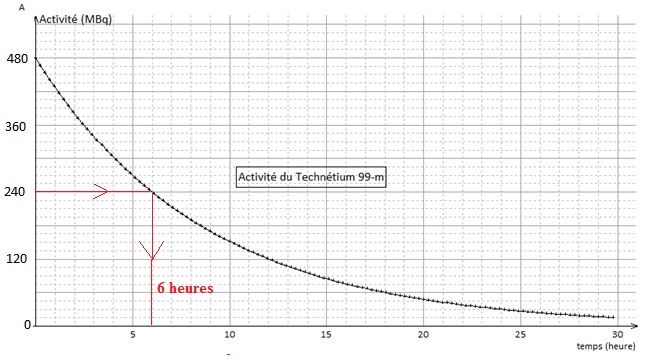
A.3.4.1. À l’aide
d’un tracé, déterminer la valeur de la demi-vie du technétium.
A.3.4.2. Il est
possible de faire subir des scintigraphies au technétium aux femmes
allaitantes à la condition d’interrompre l’allaitement pendant 24
heures. L’interruption est en revanche beaucoup plus longue avec le
thallium. Expliquer cette différence de durée d’interruption.
La demi-vie du thallium est d'environ 3 jours.
Au bout de 3 jours le lait serait encore trop radioactif. Il faut
attendre 24 / 6 = 4 demi-vies afin que la radioactivité ait
suffisamment diminuée.
Dans ce cas la durée d'interruption serait de 3 x 4 = 12 jours.
|
....
.....
|
PARTIE B : des choix technologiques pour
réaliser le coeur artificiel
La conception d’un coeur artificiel est un projet
qui date d’un
demi-siècle et qui a déjà mobilisé nombre de cardiologues et
d’ingénieurs du monde entier, vu le véritable défi technologique en jeu.
B.1. Exemple de
défi technologique : la batterie
Données :
Température : 0°C = 273 K ; Pression : 1 bar = 105 Pa
Capacité d’une pile : Q = ne-x F
Q : capacité ou quantité d’électricité disponible en coulombs (C)
ne- : quantité maximale d’électrons pouvant circuler en
moles (mol)
F : constante de Faraday = charge d’une mole d’électrons ; F = 9,65.104
C.mol-1
On rappelle que l’énergie stockée dans une pile correspond au produit
de la quantité d’électricité disponible par la tension aux bornes de
cette pile ou force électromotrice.
B.1.1. Choix de la
technologie de l’alimentation du coeur
Le coeur artificiel a besoin d’une source d’énergie afin de pouvoir
exercer son rôle de pompe du sang. Les premières batteries utilisées
pour le coeur artificiel ont été des batteries lithium-ion. Mais depuis
on cherche à remplacer la batterie lithium-ion par des piles à
combustible.
B.1.1.1. Pour
quelles raisons souhaite-t-on remplacer la batterie lithium-ion par une
pile à combustible ?
Leur masse est d'environ 6 kg et il faut les recharger toutes les 4
heures.
Il faut augmenter l'autonomie et diminuer leur masse.
B.1.1.2. Les
réactifs de la pile à combustible sont d’une part le dihydrogène H2
et d’autre part le dioxygène O2 de l’air. Les couples
oxydant-réducteur mis en jeu pour cette pile sont H+/ H2
et O2/H2O.
B.1.1.2.1. La demi-équation du couple O2/ H2O
s’écrit :
O2 + 4 H+
+ 4e- =2H2O.
Recopier sur votre copie en complétant et en équilibrant cette
demi-équation.
La demi-équation équilibrée du couple H+/ H2 est H2
= 2 H+ + 2 e-
B.1.1.2.2. En
déduire l’équation globale modélisant le fonctionnement de cette pile.
O2 + 4 H+
+ 4e- =2H2O.
2H2
= 4 H+ + 4 e-
Ajouter et simplifier : O2
+ 2H2 =2H2O.
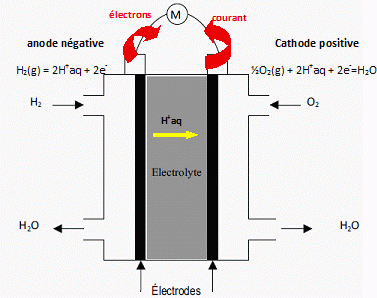
B.1.1.2.3. L’électrode où arrive le
dihydrogène est-elle l’anode ou la cathode ? Justifier.
Le dihydrogène est le réducteur qui s'oxyde. L'électrode où il arrive
est l'anode négative.
B.1.1.2.4. Préciser
le nom et le signe de chaque électrode, indiquer le sens de circulation
du courant électrique et celui des électrons.
|
|
|
B.1.2.
Fonctionnement de la pile à combustible
B.1.2.1.Quelle énergie doit être fournie par la pile à
combustible pour que son autonomie soit de 12 heures ? Exprimer le
résultat en W.h, puis en J. Puissance de la pile : 27 W.
Energie = 27 x12 = 324 Wh ou
324 x3,6 103 = 1,1664 106 ~1,2 106 J.
B.1.2.2. La tension
aux bornes de la pile est de 4,0 V.
En déduire que la capacité en coulomb (C) est de l’ordre de 2,9.105
C.
Q = 1,1664 106
/ 4 ~2,9.105 C.
B.1.2.3.
En utilisant notamment la ½ équation associée au couple H+/ H2,
vérifier que la quantité de matière de dihydrogène à stocker dans la
pile à combustible afin d’atteindre l’autonomie voulue est nH2
= 1,5 mol.
ne-
=Q / F = 2,9 105 /(9,65 104) ~3,0 mol.
nH2
=0,5 ne-
=1,5 mol.
B.1.3. Le stockage du
dihydrogène
On donne le diagramme pression – température du dihydrogène.
Pour une température ambiante de 20 °C :
B.1.3.1. Calculer
cette température en kelvin (K).
20 +273 = 293 K.
B.1.3.2. À cette
température, sous quelles formes peut-on stocker le dihydrogène ?
Justifier.
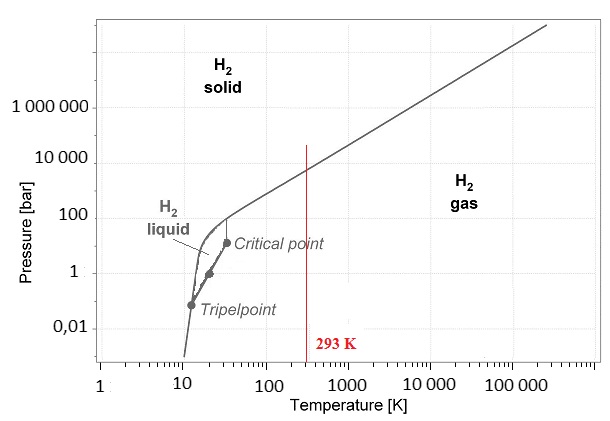
Le dihydrogène peut être solide
ou gazeux.
B.1.3.3. À cette
température, en déduire la forme sous laquelle se trouve le dihydrogène
contenu dans le réservoir à hydrogène ( P = 12 bar ).
Pour une pression de 12 bars, le dihydrogène est gazeux.
B.1.3.4.
Connaissant la pression p d’un gaz et le volume V qu’il occupe à une
température T donnée, il est possible de calculer sa quantité de
matière nH2, grâce à la loi des gaz parfaits :
pV = nRT
Avec p : pression en Pa ; V : volume en m3 ; n : quantité de
matière en mol ; T : température en K ;
R : constante des gaz parfaits ; R = 8,31 J.K-1.mol-1
Calculer, à la température de 20 °C, la quantité de matière nH2
de dihydrogène maximale que l'on peut stocker dans la bouteille de
dihydrogène. P = 1,2 106 Pa ; V = 0,8 L = 8 10-4 m3.
nH2 = PV / (Rt) = 1,2 106 x8 10-4
/(8,31 x293)=0,394 ~0,39 mol.
B.1.3.5. Le
réservoir Hy-can du document B3 permettra-il de répondre à l’objectif
d’autonomie de 12 heures pour l’alimentation du coeur artificiel ?
Non, 0,39 est inférieur à 1,5 mol, quantité nécessaire pour une
autonomie de 12 heures..
|
|
|
|
B.2. Un autre défi technologique : le choix
du capteur de pression
« Pour pouvoir adapter très finement le débit
sanguin aux
besoins physiologiques qui varient à l’effort, au repos ou lors de
changement de position, le coeur artificiel CARMAT bénéficie d’une
microélectronique de pointe. Élément central du dispositif, un
microprocesseur doté d’algorithmes qui modélisent le fonctionnement
d’un coeur naturel. En fonction des informations fournies par trois
capteurs de pression, deux capteurs à ultrasons et un accéléromètre, le
microprocesseur adapte le pilotage des deux groupes motopompes en temps
réel. »
Extrait de La Recherche, janvier 2012, N°459
Données :Pression : 1 bar = 105 Pa. 1 mmHg = 133,3 Pa (le
mmHg est le millimètre de mercure (Hg))
Une société a développé des capteurs de pression pour des applications
médicales.
Le capteur physiologique utilisé est spécialement conçu pour la mesure
de la pression intravasculaire.
Le capteur est plaqué or et fournit une tension électrique qui varie en
fonction de la pression. Les valeurs extrémales admises sont de 0 et
300 mmHg.
B.2.1. Préciser
quelles sont les grandeurs d’entrée et de sortie de ce capteur.
Grandeur d'entrée : pression ;
grandeur de sortie : tension.
B.2.2. Les valeurs
de pression dans le ventricule gauche du coeur :
Pression minimale : 5 mmHg ; Pression maximale : 180 mmHg.
Le capteur est-il adapté au suivi de la pression dans le ventricule
gauche ? Justifier.
Oui, les valeurs extrémales admises sont de 0 et 300 mmHg.
B.2.3. Pour une
pression mesurée pm = 180 mmHg dans le ventricule gauche,
déterminer un encadrement de la pression réelle pr en tenant
compte de la l’incertitude Dp
du capteur : Dp =
0,5 % de l'étendue de mesure.
Dp =
0,005 x300 =1,5 ~ 2 mm Hg.
pm = 180 ±2 mmHg.
Partie C : Et le coeur
artificiel prend vie…
Le deuxième homme greffé faisait du vélo de route huit mois après son
opération !! .
On suppose qu’il partait 20 minutes, en roulant sur du plat à la
vitesse constante de 15 km.h-1.
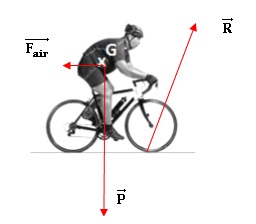
C.1. Les forces
extérieures exercées sur le cycliste et son vélo sont les suivantes :
le poids P, la réaction de la route R, la force de frottement Fair
de résistance de l’air
Représenter sans souci d’échelle, les forces exercées sur le système
{cycliste – vélo} lors de son déplacement.
Dans la suite du sujet on souhaite déterminer si le coeur artificiel
permet d’assurer un débit suffisant en cas d’effort sportif.
On admet que l’énergie nécessaire pour réaliser cinq kilomètres en vélo
à la vitesse de 15 km.h-1 est de l’ordre de 110 kJ.
C.2. Au repos, un
individu consomme à peu près une énergie de 70 J.kg-1.min-1.
Calculer l’énergie que consomme durant 20 minutes, un homme de 80 kg au
repos. En déduire que l’énergie totale consommée par cet homme roulant
à 15 km/h à vélo pendant 20 minutes doit être de 222 kJ.
70 x80 x20 =1,1 105 J = 1,1
102 kJ au repos.
112 +110 = 222 kJ à vélo.
C.3. Dans
l’organisme, le dioxygène respiré sert à « brûler » le glucose C6H12O6
obtenu grâce à la digestion des sucres et glucides.
Ecrire l’équation équilibrée modélisant la combustion complète du
glucose dans le dioxygène.
C6H12O6 +
6O2 ---> 6 CO2 +
6H2O.
C.4. On admet que
la combustion d’une mole de glucose permet d’obtenir une énergie
utilisable de 1270 kJ. Calculer la quantité de matière de glucose
nécessaire pour les 20 minutes d’efforts du cycliste.
222 /1270 =0,175 mol.
C.5. Montrer que la
quantité de matière de dioxygène consommée pendant cet effort est de
l’ordre de nO2 = 1 mol.
nO2 = 6 x 0,175 = 1,05 ~ 1,0 mol.
C.6. On admet que
seul 65 % du dioxygène présent dans le sang est utilisé et consommé par
l’organisme, et qu’il y a 0,3 g de dioxygène transporté par litre de
sang.
Calculer le débit minimum du coeur artificiel permettant un apport en
dioxygène suffisant pour cet effort.
Le coeur artificiel peut-il soutenir une telle activité physique ?
0,3 x0,65 = 0,195 g L-1 ; 1 mole de dioxygène a une masse de
32 g.
Volume de sang : 32 / 0,195 ~164 L durant 20 minutes.
Débit : 164 / 20 ~8,2 L min-1.
Le débit sanguin de ce coeur pourra atteindre jusqu’à 9 L.min-1,
cette activité physique peut être soutenue.
|
|