Sports extrèmes,
bac
Sti2d et Stl Antilles 2017 .
|
|
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
|
|
|
|
PARTIE A –Mécanique du saut en chute libre »
Une parachutiste saute d’un avion à une altitude de
4,5 km. Pour simplifier, on ne considèrera
que le mouvement vertical et la vitesse initiale sera supposée nulle.
La montre connectée de la parachutiste a permis d’obtenir l’évolution
de son altitude et de sa vitesse lors du saut. Elles sont représentées.
Deux phases se distinguent ; elles seront étudiées successivement.
Données
Masse du parachutiste avec équipement :m'=80 kg.
Volume du parachutiste : V = 70 10 -3 m 3.
Masse volumique de l’air : r
= 1,2 kg m -3.
Intensité de la pesanteur : g = 9,8 m s -2.
Altitude de départ : z = 4,5 km.
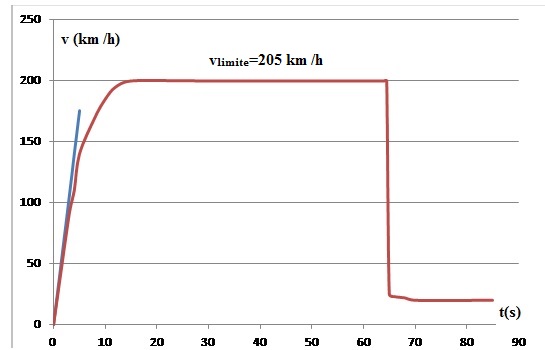 A.1
A.1 Première phase
: 0 < t < 3 s
A.1.1 Donner les
caractéristiques (direction, sens, norme et point d’application) du
poids qui s’applique sur la parachutiste.
Le poids s'applique au centre d'inertie du parachutiste ; sa direction
est la verticale ; son sens, vers le bas et sa norme vaut P = mg = 80
x9,8 = 784 ~7,8 10 2 N.
A.1.2 Montrer que
l’on peut négliger la poussée d’Archimède qui s’applique sur la
parachutiste.
La poussée d’Archimède peut se calculer par :
F = rair
g V =1,2 x70 10 -3 x9,8 ~0,82 N.
F est très inférieure au poids. F est négligeable devant le poids.
A.1.3 Justifier que
l’on peut négliger la force de trainée pendant cette première phase.
F x=0,5 rair
S C x v 2.
avec :
v : vitesse du solide en m s-1,
S : surface frontale ou maitre couple en m 2
C x : coefficient sans unité reflétant l’aérodynamisme
Au début de la chute, la vitesse est suffisamment faible pour que la
force de trainée soit négligeable devant le poids.
A.1.4 Rappeler
l’expression mathématique du principe fondamental de la dynamique.
Montrer que la valeur de l’accélération de la parachutiste pendant
cette première phase est a = g.
Le parachutiste n'est soumis qu'à son poids. Sur un axe vertical
orienté vers le bas le principe fondamental de la dynamique s'écrit :
ma = mg soit a = g.
A.1.5 On modélise
la courbe par la droite en bleu ; comment qualifier le mouvement lors
de cette première phase ?
Chute libre verticale accéélérée.
A.1.6 Montrer que
l’on peut estimer la distance d 1, parcourue par la
parachutiste pendant les 3 premières secondes, à environ 44 m.
Données
Pour un mouvement rectiligne uniformément accéléré :d = 0,5 at 2
+v 0t.
avec ici v 0 = 0 ; d 1 = 0,5 x9,8 x3 2
~44 m.
|
....
.....
|
Remarque : la deuxième phase (3 s
< t < 15 s) est trop délicate à étudier ici.
A.2 Troisième phase
: 15 s < t < 64 s
A.2.1 Comment
qualifier le mouvement de la parachutiste pendant la troisième phase ?
La valeur de la vitesse étant constante, le mouvement est rectiligne
uniforme.
A.2.2 Nommer les
forces non négligeables qui agissent pendant la troisième phase de la
chute. Le terme de « chute libre », au sens du physicien ou de la
physicienne,
correspond au cas où un objet n’est soumis qu’à l’action de la
pesanteur. La
parachutiste est-elle en « chute libre » au sens de la physique ?
Le poids et la trainée agissent sur le parachutiste. Le mouvement n'est
pas une chute libre.
A.2.3 On montre que
la distance d2, parcourue par la parachutiste pendant la
troisième phase peut s’évaluer par d2 = vlimite ×
(t − 15) où t représente le temps, en s, et vlimite, la
vitesse limite en m s-1. Montrer que la distance parcourue
pendant cette phase, jusqu’à l’ouverture du parachute, peut s’estimer à
d2 ≈ 2,8 km.
vlimite = 205 / 3,6 = 56,94 m /s.
d2 = 56,94 (64-15) ~2790 m ~2,8 km
A.2.4 Sachant que
la parachutiste a parcouru environ 550 m pendant la deuxième phase, en
déduire la distance totale d3,
parcourue lors de la chute, c’est-à-dire jusqu’à ouverture du
parachute. Le résultat est-il en accord avec le relevé altimétrique ?
Justifier.
d3 ~44 +2800 +550 ~ 3,4 103 m.
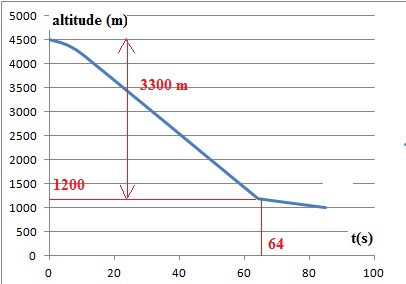
Le résultat est en accord avec le relevé altimétrique.
A.2.5 En appliquant
le principe fondamental de la dynamique à la parachutiste, montrer
que l’intensité de la trainée vaut Fx
=785 N.
Le poids est opposée à la
trainée ; ces deux forces ont la même valeur. Fx = mg = 7,8
102 N.
A.2.6 On suppose que la parachutiste
adopte une position « étendue » (horizontale et bras
écartés) pendant toute la chute et pour laquelle la surface frontale
vaut S = 1 m2.
Déterminer avec une précision de 2 chiffres significatifs, le Cx
de la parachutiste dans cette position.
Fx=0,5
rair S Cx
v2 ; Cx
=Fx/(0,5
rair
S v2 )=785 /(0,5 x1,2 x56,942)
~0,40.
A.2.7 En déduire la forme à laquelle
la parachutiste peut être assimilée.
Ce coefficient de trainée correspond à la forme en demi-sphère.
|
|
|
PARTIE
B – Dispositif automatique de déclenchement du parachute.
Plusieurs dispositifs existent pour déclencher automatiquement le
parachute de secours en cas
de problème lors d’un saut en « chute libre ». On étudie ici le
principe de fonctionnement d’un
de ces systèmes, le Cypres.
Données :
Le jour du saut, la pression au niveau du sol est Patm =
1013 hPa.
B.1 À partir de
quelle altitude le dispositif de sécurité est-il en mesure de se
déclencher ? En
déduire la pression de l’air à cette altitude.
L'appareil agit dès que la vitesse de chute du parachutiste dépasse 35
m/s à partir de 225 mètres.
Plus on s'élève en altitude, moins il y a d'air au-dessus de nos têtes
et donc plus la pression baisse. En moyenne, la pression atmosphérique
diminue de 1 hPa tous les 8 mètres.
Soit une diminution de 235 / 8 ~28 hPa.
La pression de l'air est alors 1013-28 =985 hPa.
B.2 En
fonctionnement normal, la parachutiste déclenche son parachute avant
d’atteindre cette altitude dangereuse et vole sous voile à une vitesse
de chute de 20 à 40 km /h
jusqu’à l’atterrissage. Justifier que le dispositif de sécurité ne se
déclenche pas une fois passée cette altitude.
40 /3,6 ~11 m/s, valeur inférieure à 35 m/s. Le parachute
de secours ne se déclenche pas.
B.3 Les
caractéristiques du capteur de pression du système sont données.
Identifier la grandeur d’entrée, E, et la grandeur de sortie, S, du
capteur en précisant leurs unités.
Le capteur de pression capte une pression ( hPa) en entrée et restitue
en sortie une tension (V), image de la pression.
B.4 Déterminer la
plage des altitudes sur laquelle le capteur fonctionne correctement.
Justifier.
300 à 1100 hPa.
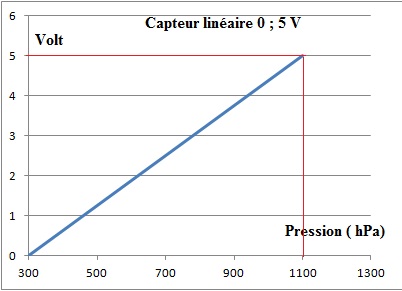
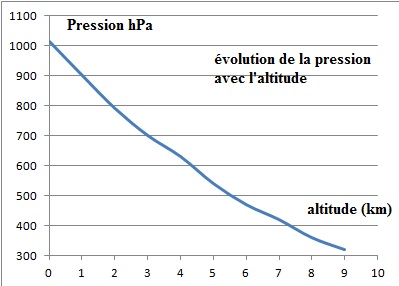
Altitudes correspondantes : 9 km ; niveau de la mer.
B.5 Déterminer l’incertitude
sur l’altitude, en mètres, due à la précision du capteur ?
Précision du capteur : ±0,03 hPa.
Or 1 hPa correspond à 8 m ; par suite précision sur l'altitude : ± 8
x0,03 = ±0,24 m.
B.6 Montrer que la
sensibilité du capteur, définie par s= Dentrée / Dsortie
, vaut s = 6,25 mV hPa
s = DU / DP = 5 / (1100-300) =6,25 10-3
V hPa-1.
|
|
|
|
B.7
La grandeur de sortie du capteur est envoyée dans le microcontrôleur
via un convertisseur analogique numérique (CAN) dont les
caractéristiques sont :
Résolution : 12 bits ; Valeurs d’entrée : 0 … 5 V
Déterminer le pas, p (parfois appelé quantum), en volts, du
convertisseur défini par :
p = Plage des valeurs de la grandeur analogique / (2n-1) =5
/ (212-1)=1,22 10-3 V.
En déduire l’incertitude sur la mesure de la pression due à l’altitude
par ce CAN 12 bits.
1,22 10-3 / (6,25 10-3) =0,1952 ~0,20 hPa.
PARTIE C – Chargeur
portable autonome.
Le parapente ascensionnel se pratique en pleine nature, parfois loin de
zones habitées. Il est donc important de pouvoir recharger son
téléphone portable pour prévenir les secours le cas échéant. Le
chargeur portable s’inscrit peu à peu dans la liste des indispensables
du sac d’un
nomade. L’énergie électrique n’étant pas disponible en toutes
circonstances, cet appareil peut être très utile en cas de déconvenues.
Dans cette partie, on étudie le chargeur USB autonome pour téléphone
portable.
C.1 Étude du
panneau solaire du chargeur autonome
Données
Surface de l’ensemble des cellules : 15 cm x 7 cm.
Tension nominale :5,0 V
Intensité nominale : 400 mA
Conditions d’éclairement lors du tracé de la caractéristique : 1000 W m-2.
C.1.1 Compléter le
schéma correspondant à la conversion de puissance assurée par le
panneau solaire, en précisant la forme de
la puissance absorbée, Pa, et celle de la puissance utile, Pu.
Pa : puissance rayonnante solaire ; Pu :
puissance électrique ; Pertes thermiques.
C.1.2 La
caractéristique intensité tension du panneau est donnée. Relever les
valeurs de la tension à vide, Uv, puis de
l’intensité du courant du court-circuit, Icc.
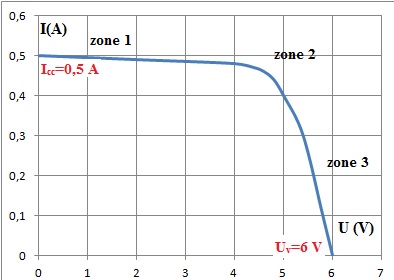
C.1.3 Que valent
les puissances fournies, Pv et Pcc, par le
panneau sur les points de fonctionnement à vide et en court-circuit ?
Justifier.
Pv = Uv Iv = 6 x0 =0 ; Pcc
= Uc Ic = 0 x0,5 =0.
C.1.4 Sur quelle
zone de la caractéristique (1, 2 ou 3 d) le panneau fournit-il sa
puissance maximale, Pmax ?
Montrer qu’elle vaut approximativement Pmax ~2,0 W.
zone 2, U ~5 V et I ~0,4 A ; Pmax = 5 x0,4 ~2,0 W.
C.1.5 En s’aidant
de la caractéristique, compléter le document en indiquant les
valeurs lues sur les appareils de mesure lors de chaque
manipulation.
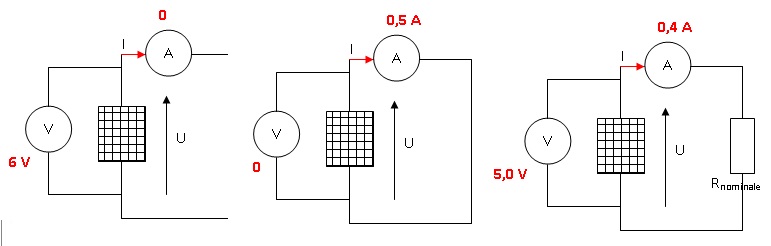
C.1.6 Montrer que
le rendement maximal du panneau photovoltaïque vaut 19 %.
Pu / Pa avec Pa = 1000 x0,15 x0,07 =
10,5 W.
Pu / Pa =2,0 /10,5 ~0,19 ( 19 %).
|
C.2
Étude de la batterie lithium ion
La batterie embarquée dans le chargeur est une batterie de type lithium
ion. Nous étudierons ici la phase de décharge.
C.2.1 Indiquer quel
intérêt offre la batterie lithium ion, notamment pour le cas du
chargeur autonome étudié ?
L'énergie volumique et l'énergie massique sont très élevées.
C.2.2 L’énergie
chimique accumulée dans la batterie est de Wchim = 90 kJ.
Estimer la masse de la batterie. Est-elle en accord avec les données
techniques du chargeur solaire.
Justifier.
150 à 190 Wh kg-1 ; 150 Wh = 150 x3,6 =540 kJ ; 190 Wh
= 190 x3,6 = 684 kJ.
Soit une masse comprise entre : 90 /540 ~0,17 kg et 90 /684 ~0,13 kg.
En accord avec la masse du chargeur (270 g).
C.2.3 Indiquer les
demi-équations des réactions qui ont lieu sur chaque électrode en
précisant s’il s’agit de l’oxydation ou de la réduction, le sens de
circulation des électrons, celui du courant électrique et le signe de
chaque électrode.
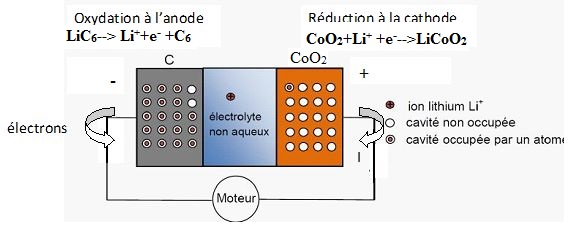
C.2.4
Écrire l’équation bilan de la réaction d’oxydo-réduction qui a lieu
lors de la décharge.
LiC6 +CoO2 -->C6 +LiCoO2.
|
|