Le passeur fluvial
Nouch,
bac
Sti2d Stl Polynésie 2017.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
|
Les
batteries lithium fer phosphate et les cellules photovoltaïques.
A.1 Intérêt des batteries
lithium fer phosphate (LFP)
A.1.1 Citer au moins trois avantages
et au moins un inconvénient des batteries LFP.
Avantages
: plus sûres que les batteries lithium-ion traditionnelles.
Large plage de température d'exploitation.
Résistance interne faible et efficacité élevée.
Il n'est pas nécessaire de les charger complètement.
Inconvénients
:
Moindre énergie stockée par kg par rapport à une batterie lithium-ion.
Coût élevé par Wh.
A.1.2
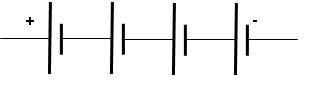
Représenter le schéma électrique d’une batterie LFP de 12,8 V constituée de cellules de 3,2 V, chacune
symbolisée par un générateur de courant continu.
4 cellules sont connectées en série.
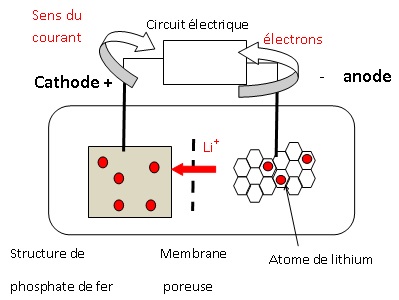
A.2 Fonctionnement de la
batterie LFP
En fonctionnement, la batterie se décharge. Il se produit alors les
réactions suivantes aux électrodes.
Cathode :
Formation de phosphate de fer lithié LiFePO4 selon
l’équation suivante :
Li+ + e- +FePO4 ---> LiFePO4.
Anode :
Libération des ions lithium qui étaient « piégés » dans les sites de
carbone, selon l’équation suivante :
LiC6 ---> 6 C +Li++e-.
A.2.1 Attribuer à
chaque électrode, cathode et anode, le type de réaction s’y produisant,
oxydation ou réduction.
Réduction à la cathode et oxydation à l'anode.
A.2.2 Écrire
l’équation bilan de fonctionnement de la batterie en décharge.
FePO4 +LiC6 ---> LiFePO4 + 6C.
A.2.3 Indiquer le trajet des ions
lithium, Li+, à travers la membrane séparant les deux
compartiments de la batterie, pendant le fonctionnement en décharge.
A.2.4 Indiquer le
sens des électrons dans le circuit électrique, le sens du courant
électrique ainsi que la polarité des électrodes.
A.3 Les panneaux
photovoltaïques.
A.3.1 Dans un des
tableaux figurent deux erreurs scientifiques de vocabulaire :
Capacité : 60 kW. h
Poids 600 kg.
Proposer des termes plus corrects pour
les corriger.
60 kWh représente une
énergie et 600 kg une masse.
A.3.2 Pour une
production moyenne des cellules photovoltaïques de 600 Wh m-2
par jour, déterminer l’énergie électrique produite par l’installation
photovoltaïque du passeur NOUCH par jour.
Surface des panneaux photovoltaïques : 12 m2.
600 x 12 = 7200 Wh.
A.3.3 Donner une
définition du rendement, h,
des cellules photovoltaïques.
Montrer que ce rendement, pour une production moyenne de 600 Wh m-2
par jour, est de 16 % aux Sables d’Olonne.
Rendement = énergie électrique disponible / énergie solaire reçue.
Energie solaire moyenne reçue par jour et par m2 : 3,8 kWh m-2
jour-1.
h =
0,600 / 3,8 =0,157 ~0,16 ( 16 %).
A.3.4 Calculer le
rendement minimal, hmini,
et le rendement maximal, hmaxi, des cellules photovoltaïques
correspondant à leurs variations de production quotidienne entre 200 Wh
m-2 par jour et 1000 Wh m-2 par jour, toujours
aux sables d’Olonne.
hmini=0,2
/ 3,8 ~0,052 ( 5,2 %) et hmaxi=1
/ 3,8 ~0,26 ( 26 %).
A.3.5.Commenter
le résultat de la question A.3.3, en justifiant la phrase du texte
d’introduction « installation photovoltaïque à haut rendement ».
Rendement des cellules photovoltaïques dans les conditions standard:
Silicium amorphe : 7 à 8 % ;
Silicium polycristallin : 11 à 13 %.
Silicium monocristallin : 14 à 16 %.
Hybride 17 à 19 %.
Ce type de cellules photovoltaïques sont parmi celles qui donnent un
rendement élévé.
|
|
|
|
Partie
B. Un passeur zéro émission.
Cette partie a pour objectif d’estimer le gain en gaz d’émission CO2
à chaque traversée grâce au passage à la propulsion électrique.
Nous considérerons que chaque traversée se fait à plein, c’est-à-dire
que la capacité maximale de passagers est atteinte.
B.1 Questions préliminaires.
La constitution du gazole
B.1.1 Expliquer en
quelques mots l’expression « passeur zéro émission ».
Le remplacement des moteurs thermiques par des moteurs électriques (
énergie électrique fournie par les panneaux solaires), fait que
le passeur n'émet aucun gaz à effet de serre et aucune particules fines.
B.1.2 Expliquer
pourquoi la masse volumique du gazole n’est pas fixée, mais peut varier
dans une fourchette de valeurs.
Le gazole est constitués d'hydrocarbures comptant environ 16 atomes de
carbone. La compositions d'un gazole est donc variable.
B.1.3 Donner un
encadrement de la température d’ébullition du gazole.
Température d’ébullition à la pression atmosphériquede l'hexadécane :
286,87°C
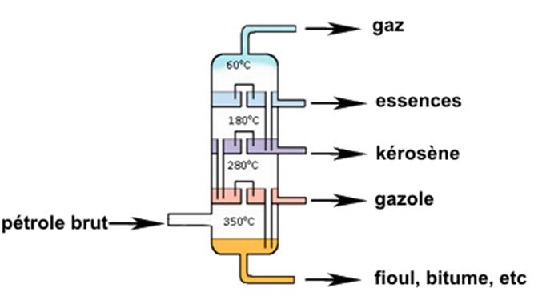
La température d'ébullition du gazole est comprise entre 280 et 350°C.
B.2 Propriétés de
l’hexadécane.
La température d’ébullition précise de l’hexadécane a été mesurée à
l’aide d’une sonde de température PT100 de classe A.
B.2.1 Compléter le
schéma du transducteur PT100 en précisant les grandeurs physiques
d’entrée et de sortie.

B.2.2 Donner un
encadrement de la température d’ébullition de l’hexadécane en tenant
compte de l’incertitude de la sonde U(T) = ± 0,15°C.
286,87 ± 0,15 soit [ 286,72 ; 287,02 °C ].
B.2.3 En utilisant
la relation du capteur PT100 ( T =2,597 R -259,7) et en tenant compte
de l’incertitude sur la température, retrouver par le calcul les
valeurs suivantes de l’encadrement de la résistance mesurée par la
sonde.
210,40 ohms < R < 210,52 ohms.
R = (T +259,7) / 2,597.
Rmini = (286,72 +259,7) / 2,597 = 210,40 ohms.
Rmaxi = (287,02
+259,7) / 2,597 = 210,52 ohms.
|
|
|
|
B.3 La
combustion du gazole
Pour la suite, on considérera que le gazole est constitué exclusivement
de l’hydrocarbure hexadécane C16H34.
B.3.1 Reproduire et
ajuster sur votre copie l’équation de combustion complète du gazole :
C16H34 + 24,5 O2 → 16 CO2 + 17 H2O.
B.3.2 Calculer
l’énergie produite par la combustion de 20 L de gazole. Détailler soigneusement les calculs et
donner le résultat en MJ, puis en kWh
Masse volumique
moyenne 850 g /L ; pouvoir calorifique moyen 44,8 MJ / kg.
Masse : 20 x0,850 = 17 kg ; énergie produite : 17x44,8 = 761,6 MJ ~7,6
102 MJ.
761,6 MJ = 7,6 105 kJ ou 7,6 105 / 3600 =211,5
~2,1 102 kWh.
B.3.3 Commenter
alors la phrase suivante :
« Une batterie de 200 kW.h en LiFePO4 correspondant à une technologie
sûre et accessible financièrement permet de remplacer 20 litres de
gazole pour fournir la même énergie ».
Cette phrase confirme le résultat précédent.
B.3.4 Par un
calcul que vous détaillerez, montrer que la quantité de matière
contenue dans 20 L de gazole est d’environ 75 mol.
M hexadécane = 226 g /mol.
17 103 / 226 = 75,22 ~75 mol.
B.3.5 En déduire la
quantité de matière en moles de CO2 produite par la
combustion complète de 20 L de gazole.
75,22 x16 =1203,5 ~1,2 103 mol.
B.3.6 En utilisant
le volume molaire des gaz ( 24 L / mol) , montrer que le volume de
dioxyde de carbone,
produit par la consommation de 20 L de gazole est d’environ 29 m3.
1203,5 x24 =28 884 L ~29 m3.
B.4 Gain d’émission de CO2
par traversée
B.4.1 La distance
d’une traversée est d’environ 100 m. En considérant que chaque
traversée s’effectue « à plein », c’est-à-dire
que la capacité maximale en passagers est atteinte, montrer que le
besoin énergétique d’une traversée est de 56 Wh
35 passagers ; consommation par passager 16 Wh / km.
35 x1,6 = 56 Wh.
B.4.2 Par un
raisonnement détaillé, en déduire alors que le volume de dioxyde de
carbone équivalent produit par chaque traversée avec une propulsion à
combustion, serait de 8,1 L.
Une énergie de 200 kWh produite par la combustion de 20 L de
gazole libère 29 103 L de dioxyde de carbone.
56 / (2,0 105) x29 103 =8,1 L.
B.4.3 Sachant que
le trafic est d’environ 200 traversées par jour, estimer le gain annuel
en tonnes de dioxyde de carbone du choix de la propulsion électrique.
Donnée : 1 L de CO2 a une masse d’environ 1,8 g.
8,1 x200 *365 = 5,913 105 L de CO2.
Masse : 5,913 105x1,8 ~1,06 106 g ou environ 1,1
tonnes.
|
|
PARTIE C
– L’amélioration de l'hydrodynamique
Sur un bateau, la résistance à l’avancement et la puissance nécessaire
aux moteurs augmentent fortement avec la vitesse. Il faut donc
maîtriser la vitesse pour être en mesure de
fonctionner pendant toute la journée sans recharge intermédiaire.
L’hydrodynamisme est l’équivalent de l’aérodynamisme mais dans un
fluide liquide. Pour un fluide peu visqueux, comme l’eau, et pour des
vitesses peu élevées, nous pouvons considérer que les équations de
l’aérodynamisme sont valables pour l’hydrodynamisme.
Les problèmes d’aérodynamisme existent aussi mais ils sont alors
négligeables.
Ainsi, les forces de frottements fluides, Fx, opposées à la vitesse, se
résument à l’expression mathématique Fx = 0,5 r CxS V2.
Pour améliorer l’hydrodynamisme, les choix de construction du passeur
NOUCH se sont portés sur une coque de type catamaran et en matériau
Composite Sandwich GFRP.
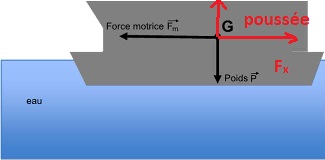
C.1 Les forces exercées
sur le passeur.
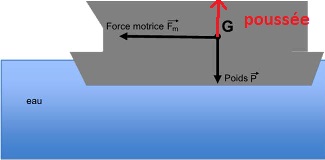
C.1.1 La force de
poussée d’Archimède compense exactement le poids du passeur. Expliquer
pourquoi et représenter vectoriellement cette force reportée au centre
de gravité de
l’ensemble.
Le bateau immobile flotte. Il est soumis à son poids et à la poussée
d'Archimède due à l'eau. Le bateau étant immobile ces deux forces sont
opposées.
C.1.2 Par une
analyse dimensionnelle, montrer que le coefficient, Cx, des
forces de frottements fluides est sans unité.
Cx
=2 Fx /( r
S v2).
Fx est une force exprimée en newton soit en kg m s-2.
r S v2 s'exprime
en kg m-3 m2 (m s-1)2 soit
kg m s-2.
Cx est donc sans dimension.
C.1.3
Représenter vectoriellement (partie démarrage la force de
frottements fluides, Fx, appliquée conventionnellement, elle
aussi, au centre de gravité de l’ensemble.
C.1.4 Expliquer en
quelques mots en quoi l’utilisation d’un catamaran plutôt qu’un
monocoque permet d’améliorer l’hydrodynamisme du passeur. Préciser sur
quel facteur l’amélioration principale est portée.
Pour un catamaran, la partie immergée est bien plus petite que celle
d'un monocoque. Le facteur CxS dans l'expression de Fx
diminue donc pour le catamaran.
C.2 La dynamique du passeur.
L’évolution au cours du temps de la vitesse du bateau, du démarrage
jusqu’à atteindre sa vitesse de croisière, peut être modélisée
simplement par la courbe suivante.
C.2.1 Identifier et
qualifier le mouvement pour chacune des deux parties distinctes de
cette modélisation.
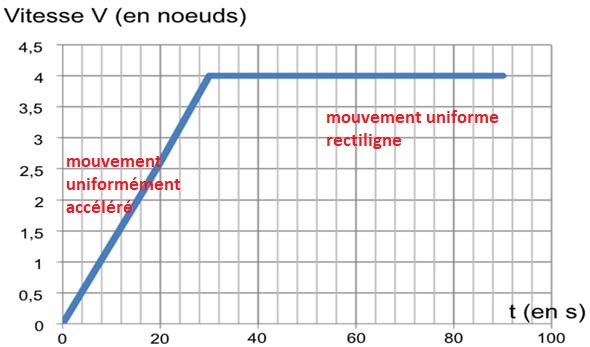
C.2.2 Évaluer
graphiquement la vitesse de croisière atteinte par le passeur NOUCH.
Exprimer cette vitesse en m /s.
Indication : 1,0 noeud = 1,85 km. h-1.
4 noeuds = 4 x1,85 km/h = 4 x1,85 / 3,6 m /s = 2,055 ~2,1 m /s.
C.2.3 Lorsque la
vitesse de croisière est atteinte, que peut-on dire des forces exercées
sur le passeur NOUCH ?
Le mouvement étant rectiligne uniforme, la somme vectorielle des forces
est nulle. Les forces se compensent.
Représenter alors soigneusement l’ensemble de ces forces (partie
vitesse de croisière.
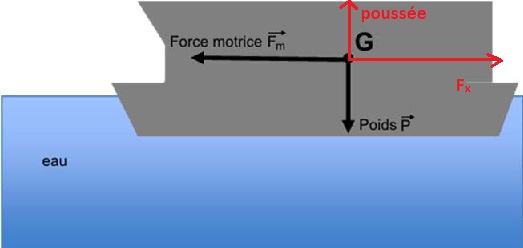
C.2.4 Evaluer
l’accélération pour l’intervalle de temps entre 0 et 30 correspondant
au démarrage.
La vitesse passe de zéro à 2,1 m /s en 30 s. l'accélération vaut : 2,1
/ 30 =0,07 m s-2.
C.2.5 En déduire
alors la valeur de la résultante des forces, sachant que la masse du
passeur en charge vaut m = 7,0 tonnes.
F = m a = 7 000 x0,07 = 4,9 102 N.
|
|