Saut spectaculaire
au dessus du canal de Corinthe.
bac S Pondichéry 2017.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
|
|
|
|
Il
a pris son élan pour accélérer sa moto et atteindre la vitesse de
125 km/h. Il a emprunté une rampe qui lui a permis de franchir le canal
et d'atterrir de l'autre côté. Le point le plus haut de son vol a
dépassé les 95 m au-dessus du niveau de l'eau.

http://wims.math.cnrs.fr/
Le
référentiel d'étude est le référentiel terrestre, supposé galiléen
pendant la durée du saut. on utilise le repère ( O, x, y ) représnté
sur la chronophotographie. A l'instant de date t=0, il se trouve à
l'origine du repère et quitte le tremplin. La vitesse initiale v0
fait un angle a
avec l'axe horizontal. L'étude est réalisée dans le cadre du modèle de
chute libre. Le pilote et sa moto sont assimilés à un point matériel de
masse supposée constante.
1. Pertinence de l'hypothèse d'une chute libre
faites par les élèves.
On étudie le mouvement suivant l'horizontale.
1. 1. Si le poids
est la seule force qui s'applique, montrer que le mouvement suivant
l'axe (Ox) est uniforme.
1.2. Valider le
modèle proposé à partir de la chronophotographie.

Les distances d3, d4,...d6, parcourues
pendant des durées égales sont égales.
Le mouvement est uniforme sur l'axe (Ox).
|
|
|
2. Vérification de la valeur
de la vitesse initiale.
On mesure quelques
abscisses des positions occupées par le morard et on calcule la vitesse
vx (m s-1) suivant l'axe l'horizontal.
28,3 ; 29,1 ; 28,7 ; 29,0 ; 27,7 ; 29,0.
2.1 Présenter le
résultat de ces mesures sous la forme vx = v x moyen
±U(Vx).
On donne U(Vx) = 2,6 x0,543 / N½.
v
x moyen =(28,3 +29,1 +28,7 +29,0 +27,7 +29,0) / 6 =28,6 m s-1.
U(Vx)
= 2,6 x0,543 / 6½=0,58 ~0,6 m s-1.
Vx = 28,6 ±0,6 m s-1.
2.2 La vitesse en
sortie du tremplin v0 = 125 km /h est-elle vérifiée sachant
que a = 33° ?
125 km /h = 125 / 3,6 = 34,7 m /s.
Vx = v0 cos a = 34,7 x cos 33 ~29,1 m s-1.
29,1 appartient à l'intervalle [28,6 -0,6 ; 28,6 +0,6 ] soit [28,0 ;
29,2 ] ; La valeur en sortie du tremplin est vérifiée.
|
|
|
..............
.................
|
3. Vérification de la hauteur du saut.
En utilisant le graphique, justifier que le mouvement suivant la
verticale est uniformément varié.
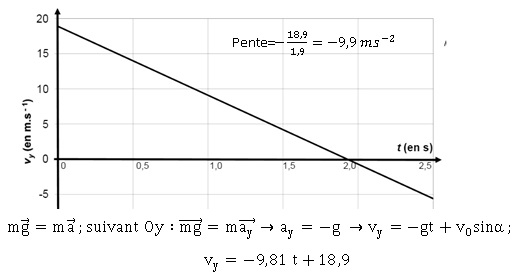
3.2.
Quelle position particulière de la trajectoire est occupée par le
motard à la date pour laquelle vy=0 ? Quelle est alors la
valeur de la vitesse à cette date ?
Au sommet de la trajectoire, la composante verticale de la
vitesse est nulle.
A cette date, la vitesse est égale à v0 cos a ~29,1 m/s.
3.3. Donner
l'expression de l'énergie mécanique du motard en fonction de la masse
m, la vitesse v, l'ordonnée y et de g.
L'origine de l'énergie potentielle de pesanteur est choisie à l'origine
O du repère.
EM = ½mv2 + mgy.
3.4 En utilisant
l'expression précédente, déterminer l'ordonnée yS du point
S, sommet de la trajectoire.
Energie mécanique initiale : ½mv02.
Energie mécanique en S : ½mv02 cos2a + mgyS.
Seul le poids travaille : l'énergie mécanique se conserve.
½mv02 cos2a + mgyS =½mv02.
v02 cos2a + 2gyS =v02.
yS =v02(1-cos2a ) / (2g) = v02sin2a / (2g) = 34,72
x sin233 / (2x9,81) = 18,2 m.
3.5. Le niveau de
l'eau est situé à 79 m au-dessous du niveau du sol. Le point de
sortie du tremplin est situé à 5,7 m au dessus du niveau du sol.
L'information suivante " le point le plus haut de la trajectoire a
dépassé les 95 m au dessus de l'eau " est-elle confirmée ?
5,7 +79 +18,2 ~103 m. L'information est vérifiée.
|
|
|
|