Mission Apollo XIV.
Bac S Centres étrangers 2017 .
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
|
|
|
|
En
février 1971, la mission américaine Apollo XIV devient la huitième
mission habitée du programme Apollo et la troisième à se poser sur la
Lune. Lors de cette mission, un des astronautes, Alan B. Shepard Jr,
installe un réflecteur de lumière sur le sol lunaire. Il réalise aussi
un rêve : jouer au golf sur la Lune !
Données :
· Célérité de la lumière dans le vide et dans l’air : c = 299 792 458
m.s-1.
· Constante gravitationnelle : G = 6,67 x 10-11 m3.kg-1.s-2.
· Valeur du champ de pesanteur terrestre : gT = 9,81 N.kg-1.
· La Terre et la Lune sont supposées sphériques.
MT = 5,98 x1024 kg ; RT = 6,38 103
km.
ML =
7,33 x1022 kg ; RL = 1,74 103 km.
1 . Mesure de la distance Terre-Lune.
Le
principe de la mesure est de déterminer la durée T d'un aller-retour
d'une impulsion LASER émise du sol terrestre vers un réflecteur lunaire
composé de nombreux prismes qui jouent le rôle de miroir. La lumière
est réfléchie dans la même direction que le rayon lumineux incident. On
en déduit la distance DTL séparant la Terre de la Lune.
La valeur moyenne de la distance DTL, étant d'environ 3,84
x108
m, on prévoit un intervalle T de quelques secondes entre l'émission
d'une impulsion et la réception du signal de retour correspondant.
Actuellement, la distance Terre-Lune peut être déterminée avec une
précision de 5 mm. D'après le site
www.culturesciencesphysique.ens-lyon.fr
1.1.
Montrer que l'information donnée dans la présentation de l'expérience
concernant la durée T est correcte. Justifier votre réponse.
T = 2DTL / c = 2 x 3,84 108 / 299 792 458=2,56 s.
Cette valeur est en accord avec "on prévoit un intervalle T de quelques secondes entre
l'émission d'une impulsion et la réception du signal de retour".
1.2. Les
incertitudes relatives sur la distance DTL et la durée T
s'expriment par la relation :
U(DTL) / DTL=U(T) / T
, où U(DTL) et U(T) sont les incertitudes absolues sur la mesure
de DTL et de T.
Le tableau ci-après donne la précision relative de quelques horloges
performantes :
Type d’horloge Horloge à quartz : 10-9 s ;
Horloge atomique au césium : 10-16 s
Horloge optique : 10-18 s.
Quel type d’horloge faut-il utiliser pour obtenir une distance DTL
précise à 5 mm près ? Justifier.
U(DTL) / DTL=5
10-3 / (3,84 108) ~1,3 10-11.
U(T) / T =1,3 10-11
; U(T) = 1,3 10-11 x2,56 ~3,3 10-11 s.
Horloge atomique au césium ou horloge optique..
2. Golf lunaire.
Interview de l’astronaute Alan B. Shepard Jr :
« - Dix ans après votre premier vol, vous êtes allé sur la Lune (Apollo
XIV, en 1971),
où vous vous êtes livré à un exercice assez original...
- Oui, j'ai joué au golf sur la Lune ! J'ai failli rater la première
balle parce que j'étais
gêné par ma combinaison spatiale et elle a lamentablement échoué dans
un cratère tout proche. La seconde, grâce à la faible gravité, est
partie à des kilomètres et des kilomètres, sans bruit, semblant ne
jamais vouloir se poser. »
D'après l'interview de F. Nolde-Langlois - 29/06/1995 - Libération
|
....
.....
|
Dans
cette partie, on souhaite vérifier quelques-uns des propos formulés par
l'astronaute lors de l'interview.
2.1. Interaction
gravitationnelle lunaire.
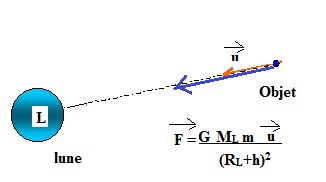
Faire un schéma d’un objet de masse m à l’altitude h au voisinage de la
Lune, en représentant :
- le vecteur unitaire u orienté de l’objet vers le centre de la Lune ;
- le vecteur F modélisant la force d’interaction gravitationnelle
exercée par la Lune sur l’objet.
Donner l’expression vectorielle de cette force d’interaction
gravitationnelle en fonction de G, m, ML, h, RL
et u.
2.2. Champ de pesanteur lunaire.
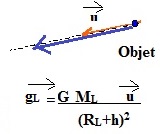
2.2.1. En faisant
l’hypothèse que le poids sur la Lune est égal à la force d’interaction
gravitationnelle, donner l’expression vectorielle gL duchamp
de pesanteur à une altitude h en fonction de G, ML, h, RL
et u.
2.2.2. Calculer la
valeur du champ de pesanteur gL à la surface de la Lune.
gL = G ML /R2L = 6,67 x 10-11
x7,33 x 1022 / (1,74 x106)2=1,6148 ~1,61 m s-2.
2.2.3. Expliquer
pourquoi Alan B. Shepard Jr parle alors de « faible gravité » sur la
Lune.
gL est environ 6 fois plus petit que la gravité au
niveau du sol terrestre.
2.3. Mouvement d'une balle
de golf dans le champ de pesanteur lunaire.
Dans cette partie, on fait l’hypothèse que le champ de pesanteur
lunaire est
uniforme et que sa valeur est gL = 1,61 N.kg-1.
On se place dans un référentiel lunaire supposé galiléen.
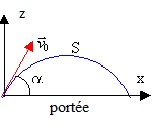
À la date t = 0 s, l’astronaute frappe la balle de golf et lui
communique une vitesse V0 faisant un angle α avec
l'horizontale.
La balle de golf est modélisée par un point matériel M.
L’origine du repère (O, i,k ) est prise au point de départ de la balle.
2.3.1. Une première
modélisation du mouvement conduit à l’expression suivante des
coordonnées du vecteur position Om de la balle lors de son
mouvement :
x(t) = V0.cos(a).t
z(t) = -½gLt2 +V0sin(a).t.
À partir des coordonnées du
vecteur position OM de la balle de golf,
montrer que dans le modèle utilisé, seule la force d’interaction
gravitationnelle a été prise en compte. Détailler la démarche suivie.
Coordonnées du vecteur vitesse à la date t, dérivée par rapport au
temps du vecteur position :
V0.cos(a) ; -gLt + V0.sin(a)
Coordonnées du vecteur accélération, dérivée par rapport au temps du
vecteur vitesse.
0 ; -gL.
D'après la seconde loi de Newton, la balle n'est soumise qu'à la
gravitation lunaire.
|
|
|
2.3.2.
Portée du coup.
La portée du coup est la distance entre le point de lancement O et le
point d’impact I au sol.
Pour une même valeur de la vitesse V0, on donne la
représentation de la modélisation de la trajectoire de la balle pour
différentes valeurs de l’angle a.
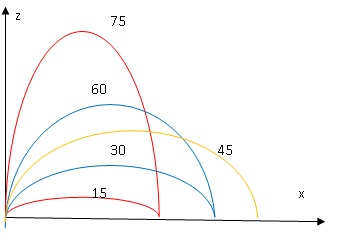
a) La portée du
coup est donnée par la relation :
x = (V0)2 .sin(2α) /gL.
En quoi cette expression est-elle cohérente avec les représentations
des trajectoires sur le graphique ci-dessus ?
La portée est maximale pour a
= 45°.
Deux angles 2a
supplémentaires ont même valeur de leur sinus.
Pour un angle de 75°, la portée est la même que pour un angle de 15°.
Pour un angle de 60°, la portée est la
même que pour un angle de 30°.
b)
Alan B. Shepard Jr se place dans les conditions les plus favorables
afin d'atteindre un record sur la Lune. Il communique à la balle une
vitesse initiale V0 de 100 km.h-1. La valeur de
la portée de son coup est alors de 470 m.
À quelle distance aurait-il pu envoyer la balle sur Terre, avec les
mêmes conditions initiales ? Commenter.
La portée est inversement proportionnelle à la gravitation.
470 x1,61 / 9,81 = 77,1 m.
|
|
|
|
3.
Communication entre la Lune et la capsule Apollo.
Quand elle arrive au voisinage de la Lune, la capsule Apollo est mise
en orbite à une altitude h égale à 110 km. Son mouvement est circulaire
et uniforme autour du centre de la Lune. Le module lunaire (LEM) est
alors envoyé sur la Lune, avec deux astronautes à son bord. Le
troisième astronaute reste à bord de la capsule Apollo.
Le schéma ci-dessous représente l’orbite de la capsule Apollo autour de
la Lune. Les échelles ne sont pas respectées.
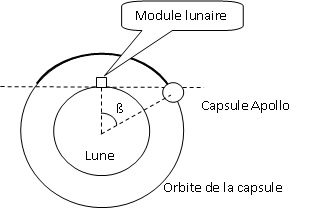
L’étude
du mouvement de la capsule se fait dans le référentiel lunocentrique
supposé galiléen, défini par le centre de la Lune supposée sphérique et
trois axes dirigés vers trois étoiles fixes. Dans cette étude, on
néglige la rotation de la lune sur elle-même dans le référentiel
lunocentrique.
3.1. Donner
l’expression de la valeur du vecteur accélération de la capsule sur
son orbite en fonction de G, ML, h, RL.
a = GML /(RL+h)2.
3.2. Montrer que la
valeur v de la vitesse de la capsule est donnée par : v =(GML
/(RL+h))½.
L'accélération est centripète ; sa valeur est égale à v2 /(RL+h).
Par suite : v2 /(RL+h) = GML /(RL+h)2.
v2 = GML /(RL+h) ; v =(GML
/(RL+h))½.
3.3. Vérifier que
la durée entre deux passages successifs de la capsule Apollo à la
verticale du module lunaire posé sur la Lune vaut environ 2 h.
v =(6,67 10-11 x7,33 1022 /(1,74 106
+1,10 105))½=1,626 103 m/s.
La capsule parcourt la circonférence 2p(RL+h à la
vitesse v en T seconde.
T = 2 x3,14 x(1,74 106 +1,10 105)/ (1,626 103)=7,15
103 s ~1,99 h ~ 2h.
3.4.
Expliquer pourquoi la communication entre les astronautes sur la Lune
et leur collègue resté dans la capsule ne peut se faire que sur la
partie de l’orbite représentée en gras.
Les ondes se propagent en ligne droite. Il ne doit pas y avoir
d'obstacles entre la capsule et le module lunaire.
3.5. Quelle est la
durée de communication possible à chaque révolution de la capsule ?
cos ß = RL / (RL +h) = 1,74 103 /(1,74
103 +110)=0,9405 ; ß =19,86 °.
2ß ~39,73° soit 39,73 / 360 ~0,1104 fraction de la période T.
0,1104 x1,99 ~0,2196 h ou 13 min 11 s.
|
|