Les ondes
gravitationnelles,
bac
S Asie 2017 .
|
|
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
|
|
|
|
Clin
d’oeil de l’histoire : c’est 100 ans tout juste après la publication de
la théorie de la relativité générale d’Einstein, qu’une équipe
internationale en a confirmé l’une des prédictions majeures, en
réalisant la première détection directe d’ondes gravitationnelles.
Données :
- Masse du Soleil : MS = 2,00 1030 kg ;
- Les ondes gravitationnelles se propagent à la célérité de la lumière
dans le vide, soit
c = 3,00 108 m.s-1 ;
- Constante de gravitation universelle : G = 6,67 10-11 m3.kg-1.s-2.
1. Les ondes
gravitationnelles détectées 100 ans après la prédiction d’Einstein
Pour la première fois, des scientifiques ont observé des ondes
gravitationnelles, produites par la collision de deux trous noirs.
Cette découverte confirme une prédiction majeure de la théorie de la
relativité générale énoncée par Albert Einstein en 1915. Ces ondes ont
été détectées le 14 septembre 2015 par les deux détecteurs jumeaux de
LIGO (Laser Interferometer Gravitational-wave Observatory) situés aux
Etats-Unis à Livingston, en Louisiane, et à Hanford dans l’État de
Washington, distants de 3000 km.
L’analyse des données a permis d’estimer que les deux trous noirs ont
fusionné il y a 1,3 milliard d’années et qu'ils avaient des masses
d’environ 29 et 36 fois celle du Soleil.
Selon la théorie de la relativité générale, un couple de trous noirs en
orbite l’un autour de l’autre perd de l’énergie sous forme d’ondes
gravitationnelles, ce qui entraîne un rapprochement des deux astres. Ce
phénomène peut durer des milliards d’années avant de s’accélérer
brusquement. En une fraction de seconde, les deux trous noirs entrent
alors en collision et fusionnent en un trou noir unique. Une énergie
colossale est alors convertie en ondes gravitationnelles. C’est cette
"bouffée" d’ondes qui a été observée.
D’après le communiqué du CNRS - 11 février 2016.
1.1
À quelle distance de la Terre, exprimée en année-lumière, se trouve la
source des ondes gravitationnelles détectées le 14 septembre 2015 ?
1,3 milliards = 1,3 109 ans .
Distance de la terre : 1,3 109 al.
1.2 Le détecteur de
Livingston a détecté les ondes gravitationnelles 7 ms avant celui de
Hanford. Cet écart a permis d’envisager des localisations possibles de
leur source.
|
....
.....
|
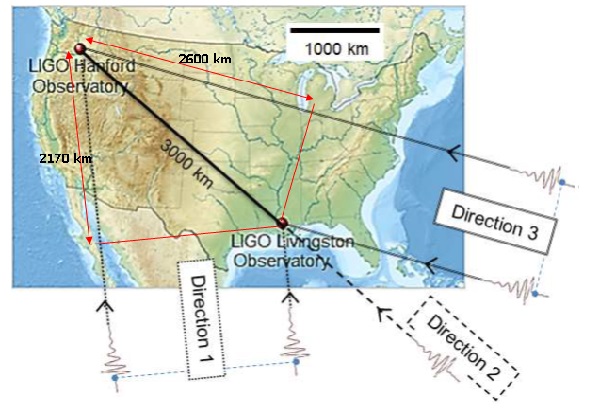
1.2.a.
Compte tenu de cet écart de détection de 7 ms, expliquer pourquoi les
ondes gravitationnelles ne peuvent pas provenir de la direction 2.
Direction 2
: 3 106 / (3 108) = 0,01 s = 10 ms, valeur
différente de 7 ms.
1.2.b. Choisir, en
justifiant, une direction possible pour leur provenance parmi les deux
autres proposées sur la carte ci-dessus.
Direction 3 : 2,6 106
/ (3 108) ~ 8,7 10-3 s = 8,7 ms, valeur
différente de 7 ms.
Direction 1
: 2,17 106 / (3 108) ~7,2 10-3 s = 7,2
ms, valeur proche de 7 ms.
La direction 1 est possible.
|
|
|
2.
Fusion de deux trous noirs.

Illustration de l’émission d’ondes gravitationnelles lors de la
rotation d’un couple de trous
noirs de même masse.
D’après une animation LIGO
Dans cette partie on fait l'hypothèse que les deux trous noirs ont la
même masse. On considère qu'ils sont sur une même orbite circulaire de
rayon r mais diamétralement opposés.
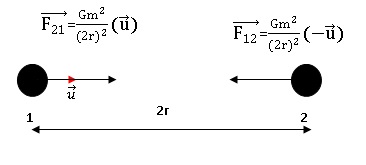
2.1 Schématiser le
système des deux trous noirs et représenter sans souci d’échelle la
force d’interaction gravitationnelle exercée par l’un des deux trous
noirs sur l’autre et donner l’expression de sa valeur en fonction de G,
m et r.
La période des ondes gravitationnelles émises est la demi-période de
révolution des trous
noirs.
.
|
|
|
|
On
se place dans le cadre de la mécanique newtonienne. Le référentiel dans
lequel les trous noirs sont en rotation est considéré galiléen. On
considère le centre de la trajectoire fixe dans ce référentiel.
2.2 Montrer que la
vitesse v des trous noirs peut s'écrire : v = 0,5 (Gm / r)½.
L'accélération de chaque trou noir est centripète Sa valeur est égale à
:
v2 /r = Gm /( 2r)2 ; v2 = Gm / (4r) ;
v = 0,5 (Gm / r)½.
2.3 En déduire que
le rayon de l’orbite est lié à la période de révolution des trous noirs
par la relation : r3 = Gm T2 / (16 p2).
Chaque trou noir décrit la circonférence 2pr en T seconde à la vitesse
v.
2pr = v T ; 4p2r2 =v2
T2 ;
4p2r2
=Gm T2 / 4r ; 16p2r3
=Gm T2 ; r3 = Gm T2 / (16 p2).
2.4 Comment évolue
la fréquence des ondes gravitationnelles émises par les deux trous
noirs quand ils se rapprochent pour fusionner ?
T et r varient dans le même sens. Si r diminue, T diminue et la
fréquence f = 1 /T augmente.
L’analyse des données indique que juste avant la fusion des deux
astres, ces derniers tournaient l'un autour de l'autre à une cadence
d’environ 75 tours par seconde. Les théoriciens tenant compte de la
relativité générale estiment alors que la vitesse de chacun est voisine
du quart de celle de la lumière.
2.5 En considérant
deux trous noirs, chacun de masse environ égale à 30 fois la masse du
Soleil, montrer que les lois de la mécanique newtonienne donnent une
bonne approximation de la vitesse des trous noirs.
f =75 Hz ; T = 1 / 75 s ; r3 = Gm T2 / (16 p2) =6,67 10-11
x30 x2 1030 /(16 x3,142 x752)=4,5
1015 ; r = 1,65 105 m.
v = 0,5(Gm / r)½ =0,5(6,67 10-11 x30 x2 1030
/ (1,65 105))½~7,8 107 m /s.
3 108 /4 = 7,5 107 m /s.
Ecart relatif : (7,8-7,5) / 7,5 x100 = 4 %.
Les lois de la mécanique newtonienne donnent une bonne
approximation de la vitesse des trous noirs.
|
|