Quand Newton vient en aide aux skateurs, bac S Antilles 09 /2017 .
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.



.
.


La finale de skateboard du FISE WORLD (Festival International des Sports Extrêmes) s’est déroulée le 5 mai 2016 à Montpellier. Parmi les nombreuses figures réalisées par les skateurs, les
enchainements de « ollie » et de « grind » se sont succédés.
Comment faire un « ollie » ?
Un « ollie » est la figure de base du skateboard. Il s'agit d'un saut effectué avec la planche (…) Pour réaliser cette figure, il faut donner un bon coup avec votre pied arrière. Il est important de bien faire claquer l’arrière de la planche ; c’est ce qui vous permet de décoller.
D’après http://fr.wikihow.com/faire-un-ollie
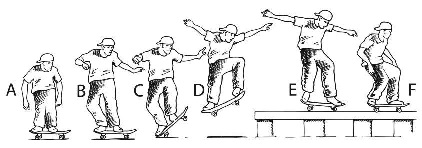
Enchainement d’un « ollie » et d’un « grind »
Le skateur avance d’abord en ligne droite à vitesse constante, puis la réalisation d’un « ollie » lui
permet d’accéder à un rail et de glisser alors sur les axes de roues et de réaliser ainsi un « grind ».
Cet enchaînement peut se décomposer de la manière suivante :

D’après Journal of Applied Biomechanics, University of Massachusetts
http://stilab.com/content/papers/kinetics-of-the-ollie-2.pdf
Données :
- hauteur du rail : h = 45 cm ;
- longueur du trajet sur le rail horizontal : L = EF = 2,0 m ;
- masse du système S {skateur + planche} : m = 75 kg ;
- intensité de la pesanteur : g = 9,8 m.s-2.
L’étude du mouvement du système S {skateur + planche} est faite dans le référentiel terrestre considéré comme galiléen.
Dans tout l’exercice, le système S, considéré comme indéformable, est assimilé à un point matériel G situé à une distance H = 1,0 m du support où se trouve le skateur, quel que soit ce support (sol, rail…). Pour toutes les phases du mouvement, on pose que l’énergie potentielle de pesanteur est nulle au niveau du sol.
Les quatre parties de l’exercice sont indépendantes.
Première partie : Parcours AB.
1.1. Quelle est la nature du mouvement du système S sur le parcours AB ?
Le skateur avance en ligne droite à vitesse constante : le mouvement est rectiligne uniforme.
1.2. Que peut-on dire, sur ce parcours, des forces exercées sur le système S ? Justifier la réponse.
D'après la première loi de Newton, la somme vectorielle des forces appliquées au système est nulle.
....

.....
 Deuxième partie : Étude énergétique du « ollie »
On s’intéresse à présent au mouvement du système S sur le parcours CE.
Le skateur effectue un «ollie» ; il quitte le sol au point C au moment où sa vitesse est vc = 3,6 m.s-1 ; il atteint le rail au point E avec la vitesse vE. On néglige les frottements sur le parcours CE.
2.1. Donner les expressions de l’énergie mécanique du système S au point C et au point E.
Au sol, l'énergie potentielle de pesanteur est nulle. L'énergie mécanique en C est sous forme cinétique et potentielle: ½mvc2+mgH.
Energie mécanique en E : ½mvE2+mg(H+h).
2.2. En sachant que l’on néglige toute forme de dissipation d’énergie entre C et F, déterminer
l’expression de la vitesse vE au point E en fonction de g, h et vc.
L'énergie mécanique se conserve entre les points C et E :
½mvc2+mgH =½mvE2+mg(H+h).
½vc2 =½vE2+gh.
vE = (vc2-2gh)½.
2.3. En déduire la valeur de la vitesse vE au point E.
vE = (3,62 -2x9,8x0,45)½=2,035 ~2,0 m s-1.

Troisième partie : Étude énergétique du « grind »
On étudie à présent le mouvement du système S qui glisse sans rouler sur le rail horizontal, du point
E au point F. Les forces de frottement ne sont pas négligeables, elles sont assimilables à une force f unique, constante et opposée au sens du mouvement.
3.1. Le document ci-après rassemble les représentations graphiques de l’évolution des grandeurs
énergie potentielle de pesanteur EP, énergie cinétique Ec, et énergie mécanique Em du système
S sur le parcours EF.
Attribuer à chaque courbe l’énergie qui lui correspond en justifiant.


L'énergie potentielle est constante ( rail horizontal) : courbe 2.
L'énergie mécanique est la somme de l'énergie cinétique ( courbe 1) et de l'énergie potentielle. L'énergie mécanique diminue du travail des frottements ( courbe 3).
3.2. Donner l’expression littérale du travail de la force f le long du parcours EF.
Travail résistant des frotterments : W = -f EF.
3.3. En utilisant la non-conservation de l’énergie en présence de frottements, en déduire la valeur
de l’intensité de la force de frottement.
L'énergie mécanique diminue de 480 à 420 J sur une distance de 2 m.
420-480 = - 2,0 f ; f = 30 N.





Quatrième partie : Étude énergétique du mouvement sur la rampe
Le skateur quitte le rail, les roues du skate sont de nouveau en contact avec le sol et roulent sans
frottement. Le skateur prend de l’élan jusqu’au point K pour aborder la rampe : la vitesse horizontale
atteinte a pour valeur vK = 4,5 m.s-1.










4. Le skateur arrive en haut de la rampe avec une vitesse nulle. Déterminer la hauteur de la rampe.
Les frottements sont nuls ; le skieur est soumis à son poids et à l'action du sol.
L'action du sol étant perpendiculaire au sol, son travail est nul.
Travail résistant du poids  en montée, entre K et le sommet de la rampe.
W = -mgH' avec H', hauteur de la rampe.
Ecrire le théorème de l'énergie cinétique entre K et le sommet de la rampe :
0-½mvK2 = -mgH'.
H' = vK2 / (2g) = 4,52 / (2 x9,8) =1,033 ~1,0 m.

.
 


  

menu