Mécanique avec le professeur Walter H.G.Lewin, bac S Antilles 2017 . En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . Le professeur utilise un pendule simple constitué d'un câble inextensible de masse négligeable, auquel est relié une boule d'acier peinte et homogène de masse m = 15 kg et de diamètre 13 cm. Le pendule est accroché au plafond de l'amphityhéatre ; la longueur L entre le plafond et le centre G de la boule est de 5,21 m. On donne g = 9,81 m s-2. 1. Première expérience. Le professeur amène la boule contre son menton. Après avoir lâché la boule sans vitesse initiale, à partir d'un angle de 41° par rapport à la verticale, celle-ci fait un aller et retour et s'approche du menton de Walter H.G.Lewin, sans toutefois le toucher. 1.1. Compléter le schéma suivant, en y reportant les mesures connues de la situation initiale au moment du lâcher. En déduire l'altitude initiale du centre G de la boule. 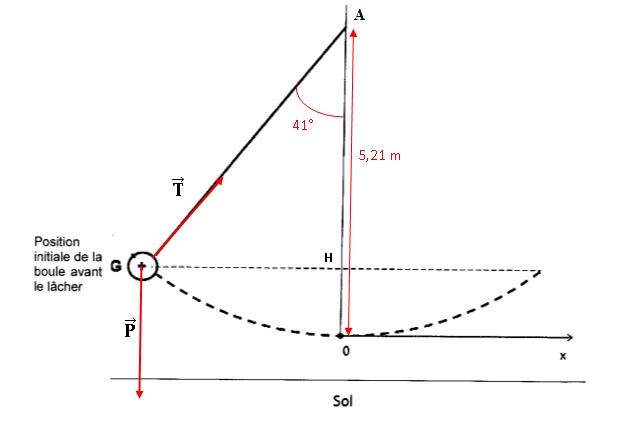AH = 5,21 cos41 = 3,932 m. Altitude initiale de G : OH = 5,21-3,932 =1,278 ~1,3 m. 1.2. Faire l'inventaire des forces qui s'exercent sur la boule et les représenter, sans souci d'échelle. On néglige toutes les forces exercées par l'air. La boule est soumise à son poids et à la tension du câble. 1.3. par convention, l'énergie potentielle de la boule au point O est nulle. Montrer que l'énergie mécanique initiale de la boule est de 1,9 102 J. L'énergie mécanique initiale de la boule est sous forme potentielle, la vitesse initiale étant nulle. E = mg OH = 15 x9,81 x1,278 = 188,0 J ~1,9 102 J. .... ..... 1.4. Quelle est la position du centre G de la boule correspondant à la vitesse maximale de la boule ? Calculer ( en km /h) la vitesse maximale de la boule. En O, l'énergie mécanique est sous forme cinétique. De plus l'énergie mécanique se conserve. E = ½mv2 ; v = (2E / m)½ = (2 x188 / 15)½ =5,0073 m /s soit 5,0073 x3,6 = 18,026 ~18 km /h. 1.5.En quoi la photographie contredit-elle l'hypothèse formulée à la question 1.2 ? Au retour, la boule s'arrète à quelques centimètres du menton. Les frottements dus à l'air ne sont pas négligeables. L'énergie mécanique de la boule diminue du travail des frottements. 2. Seconde expérience. 2.1. Première mesure. Il écarte le pendule d'un angle de 10° par rapport à la verticale. Il déclenche un chronomètre au moment où il lâche la boule sans vitesse initiale. Il compte le nombre de fois où la boule revient quasiment à la position initiale. A la dixième fois, il arrête le chronomètre qui affiche 45,81 s. L'incertitude est ±0,2 s. Il note au tableau 10 T = 45,8 ±0,2 s. 2.1.1. Donner un encadrement de la valeur de la période de ce pendule simple. T = 4,58 ±0,02 s. 2.1.2. Commenter la méthode de mesure. En mesurant un grand nombre de période, on diminue l'incertitude sur la mesure de celle-ci. 2.2. Deuxième mesure. Le professeur s'assied sur la boule et précise qu'il doit se mettre en position allongée pour ne pas fausser la démonstration. Puis de la même manière, il s'écarte afin que le câble fasse un angle de 10° par rapport à la verticale. Il se laisse balancer avec la boule et il se filme. La vidéo a été exploitée pour donner les courbes d'évolution temporelle suivantes. 2.2.1. L'une des courbes représente x(t) et l'autre y(t) ; les axes Ox et Oy sont ceux définis sur le schéma ci-dessus. Identifier les courbes en commentant leur allure.. Courbe 1 : y(t) est toujours positif. Courbe 2 : x(t) varie périodiquement de -0,9 m à +0,9 m. Les extrémums de ces courbes diminuent au cours du temps. L'énergie mécanique de la boule diminue, les frottements ne sont pas négligeables. 2.2.2. Déterminer la valeur de la période de ce pendule constitué du câble, de la boule et du professeur. 9T = 41 s ; T = 41 / 9 = 4,56 s. 2.2.3. Par une analyse dimensionnelle, vérifier l'homogénéité de l'expression de la période T = k(L /g)½ où k est une grandeur sans dimension. L est une longueur exprimée en mètre. g est une accélération exprimée en m s-2. L /g s'exprime en s2 ; (L / g)½ s'exprime en seconde. T s'exprime en seconde. l'expression est homogène. 2.2.4. Expliquer ce que le professeur a voulu démontrer dans cette expérience. Le résultat obtenu est-il concluant ? La période d'un pendule simple est indépendante de sa masse. (4,58-4,56) / 4,58 ~0,004 ( 0,4 %). Le résultat obtenu est concluant. .

menu