Performance des
matériaux de construction,
bac
S Polynésie 09 /2017 .
|
|
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
|
|
|
|
Construire
des immeubles de grande hauteur en bois est désormais possible. Jusqu’à
présent, le bois assurait les ossatures et les charpentes des maisons
individuelles. Les techniques de lamellé collé consistant à coller
entre elles des lames de bois permettaient la construction d’immeubles
collectifs de quatre étages.
Depuis quelques années, il est possible de construire des immeubles
d’une quinzaine d’étages grâce à la fabrication de panneaux porteurs
par la technique de « cross laminated timber » (CLT).
D’après le site www.sciencesetavenir.fr
Données :
Dans le cas d'une paroi formée de plusieurs couches de matériaux
différents, la résistance thermique totale est la somme des résistances
des différentes couches.
Le flux thermique F,
exprimé en watt (W), est une grandeur positive qui représente l’énergie
transférée à travers une paroi par unité de temps.
Pour une paroi plane dont les deux faces sont à des températures T 1
et T 2, le flux thermique s’exprime par la relation :
F = (T 1
− T 2) /R th où T 1 et T2 sont exprimées
en kelvin (K).
Conductivité thermique de divers matériaux :
Matériau
|
Epicéa
|
Béton
armé
|
verre
|
Air
|
Argon
|
Conductivité
thermique ( W m-1 K-1)
|
0,11
|
2,2
|
1,2
|
0,026
|
0,018
|
Dimensions d’un panneau CLT en épicéa
longueur : 6,0 m ; largeur :
3,0 m ; épaisseur : 20 cm
1. Performance thermique
de l’immeuble.
1.1. Résistance
thermique du panneau CLT en épicéa.
1.1.1. Déterminer
l’unité de la résistance thermique.
La résistance thermique Rth d’une paroi
se détermine par la relation :
Rth =e / (l×S)
λ : conductivité thermique du
matériau en W.m-1.K-1 ;
e : épaisseur de la paroi en m ;
S : surface de la paroi en m2.
Rth s'exprime en m W-1 m K m-2 soit
en W-1 K.
1.1.2. Déterminer la valeur de la
résistance thermique du panneau CLT en épicéa.
S = 6,0 x 3,0 = 18,0 m2.
Rth = 0,20 / (0,11 x 18,0) =0,101 ~0,10 W-1 K.
1.1.3. Déterminer
l’épaisseur de béton armé nécessaire pour obtenir une paroi de même
surface que le panneau CLT et ayant les mêmes performances thermiques.
Commenter le résultat.
e = Rth l
S = 0,101 x2,2 x18,0 ~4,0 m.
Il est impossible de construire un imeuble avec des parois de béton de
4 m d'épaisseur.
1.2. Les fenêtres
en bois de l’immeuble sont constituées d’un double vitrage composé de
deux feuilles de verre de 4,0 mm d’épaisseur séparées par un espace
hermétique clos renfermant 12,0 mm d'air. On étudie une fenêtre de
surface S = 4,0 m².
Règlementation en vigueur :
Le coefficient de transmission thermique U d’un vitrage doit être
inférieur à un niveau maximal réglementaire de 2 W.m-2.K-1.
Le coefficient de transmission thermique U d'une paroi homogène
multicouche est l’énergie thermique qui traverse cette paroi en régime
permanent, par unité de temps, par unité de surface et pour une
différence de température de 1° C entre la face interne et la face
externe.
1.2.1. Citer le
mode de transfert d’énergie prépondérant à travers le vitrage.
En donner une interprétation microscopique.
La conduction. L'agitation
thermique est transmise de proche en proche, sans ttransport de matière.
En se déplaçant lentement, les molécules cèdent une partie de leur
énergie cinétique par des chocs sur les autres particules rencontrées.
1.2.2. Déterminer
la valeur du flux thermique traversant la fenêtre en double vitrage
pour un écart de température de 10° C entre l’intérieur et l’extérieur
du bâtiment.
Rth =( everre / lverre +eair
/ lair)
/ S = ( 0,008 / 1,2 +0,012 / 0,026) / 4,0 =(0,00667 +0,4615) / 4,0 =
0,117 W-1 K.
Flux thermique : 10 / 0,117 ~85 W.
1.2.3. En supposant
que seul le mode de transfert d’énergie prépondérant intervient,
peut-on dire que ce vitrage respecte la règlementation ? Justifier.
U = 1 /(Rth S) = 1 / (0,117 x4) ~2,1 W.m-2.K-1.
Cette valeur étant supérieure à 2, le vitrage ne respecte pas la
réglementation.
1.2.4. Proposer, en justifiant, deux
solutions pour améliorer les performances thermiques de ce vitrage.
Remplacer l'air par de l'argon de conductivité thermique plus faible.
Rth =( everre
/ lverre
+eargon / largon)
/ S = ( 0,008 / 1,2 +0,012 /
0,018) / 4,0 ,=(000667 +0,6667) / 4,0 = 0,168
W-1 K.
U = 1/(4 x0,168) ~1,5 W.m-2.K-1.
Augmenter la surface des fenètres. Pour une surface de 4,5 m2
et une lame d'air :
U = 1/(0,117 x4,5) ~ 1,9 1,5 W.m-2.K-1.
|
....
.....
|
2. Performance acoustique de l’immeuble.
Les parois vitrées sont également des isolants acoustiques, dont la
performance est caractérisée par une grandeur appelée atténuation
acoustique (en dB).
Pour l’étude mécanique d’un double
vitrage, l’air entre les deux parois peut être modélisé par un ressort.
Les vibrations de la paroi 1, dues à l’excitation provoquée par une
onde acoustique, sont ainsi transmises à la paroi 2 avec un
affaiblissement causée par la lame d’air qui les sépare.
A une certaine fréquence critique d’excitation, correspondant à la
fréquence de résonance du système, les vibrations sont mieux transmises
et l’atténuation acoustique diminue.
Dans ce modèle, la fréquence critique fc pour un double
vitrage, exprimée en Hz, est donnée par : fc= 60 ×[ (1 /mS1+1
/ mS2) / d ]½.
d : distance entre les deux parois (en m).
mS1 et mS2 : masses surfaciques des parois de
verre 1 et 2 (en kg.m-2) ; la masse surfacique est définie
comme étant le rapport de la masse de la vitre sur sa surface.
Les doubles vitrages sont caractérisés par trois nombres qui
correspondent aux épaisseurs exprimées en millimètres de la première
feuille de verre, de la couche d’air et de la dernière feuille de
verre. Le double vitrage étudié dans la partie précédente est identifié
par 4-12-4. Quand la vitre est un simple vitrage, un seul nombre est
donné, c’est l’épaisseur de la vitre en millimètres.
2.1. Pour une vitre
d’épaisseur e, la masse surfacique mS s’exprime en fonction
de la masse volumique r
et de e par la relation : mS = r.e. Vérifier, par analyse
dimensionnelle, que cette relation est correcte.
La masse volumique s'exprime en kg m-3 et l'épaisseur en
mètre.
mS s'exprime en kg m-2.
2.2. Calculer la
valeur de la fréquence critique pour le double vitrage 4-12-4 de
surface S = 4,0 m2, sachant que la masse volumique ρ du
verre est égale à 2500 kg.m-3.
Le résultat obtenu est-il cohérent avec les courbes donnant
l’atténuation acoustique de différents vitrages en fonction de la
fréquence, reproduits ci-après ?
mS = 2500 x0,004=10 kg m-2.
fc= 60 ×[ (1 /mS1+1
/ mS2) / d ]½= fc=
60 ×[ (1 / 10+1 / 10) / 0,012 ]½= 245 ~2,4 102 Hz.
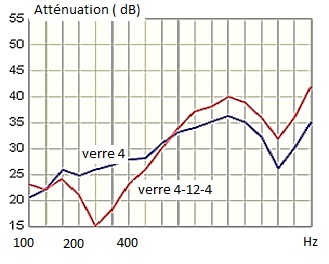
L'atténuation acoustique est minimale pour une fréquence voisine de 250
Hz pour le vitrage 4-12-4.
Donc accord du résultat avec les courbes.
2.3. Le double
vitrage présente-t-il un intérêt par rapport au simple vitrage du point
de vue de l’isolation acoustique ? Justifier.
2.4. Comment les
fabricants peuvent-ils modifier le double vitrage pour améliorer ses
propriétés acoustiques ?
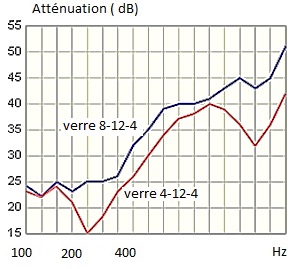
Le vitrage de type 8-12-4 posède une atténuation acoustique supérieure
au simple vitrage et au double vitrage 4-12-4 pratiquement à toutes
fréquences.
Les constructeurs doublent l'épaisseur de la première épaisseur de
verre.
|
|
|
3. Contrôle de la qualité d’isolation
thermique d’un immeuble.
Le diagnostic thermique d’un bâtiment peut être réalisé par
thermographie infrarouge. Le capteur d’une caméra infrarouge génère une
tension électrique proportionnelle à l’intensité du rayonnement qu’il
reçoit du bâtiment. Le signal est numérisé, puis transformé en points
lumineux sur un écran à l’aide d’un calculateur. La couleur de chaque
pixel de l’image dépend de la température de chaque point de l’objet.
En thermographie infrarouge, on travaille généralement dans une bande
spectrale qui s’étend de 2 à 15 μm et certaines bandes sont
privilégiées.
Extrait de la notice technique de la caméra C.A 1886 RayCAm :
- Taille d’une image en pixels : 160 x 120
- Sensibilité thermique : 0,08 ° C à 30 ° C
- Gamme de mesure : - 20 ° C à + 600 ° C (1000 ° C ou 1500 ° C en
option)
- 1000 images enregistrables sur carte MiniSD
- Torche et pointeur Laser.
 D’après le site www.ctta.fr D’après le site www.ctta.fr
|
|
|
|
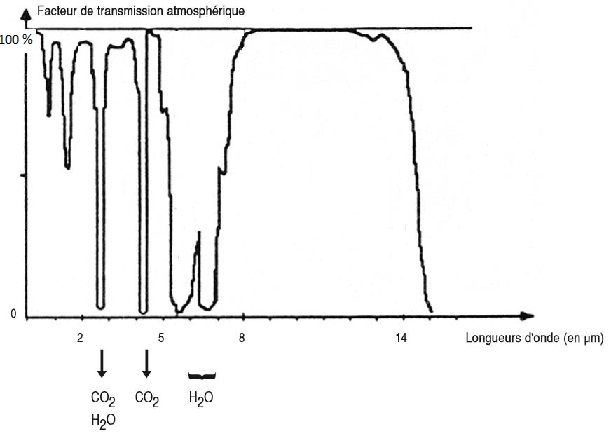
Transmission
des ondes électromagnétiques par l’atmosphère terrestre :
3.1. Identifier
l’intervalle de longueur d’onde dans lequel il est préférable
d’utiliser la caméra thermique. Justifier.
La transmission des ondes est maximale entre 8 et 14 µm.
3.2. Quel type de
convertisseur doit-on placer entre le capteur et le calculateur qui
génère l’image ?
CAN.
3.3. Sachant qu’un
pixel est codé en 24 bits, quelle serait la capacité minimale, en
octets, de la carte MiniSD en l’absence de compression ?
160 x 120 =19 200 pixels par image.
19 200 x24 =4,6 105 bits par image ou 5,76 104
octets.
5,76 107 octets pour 1000 images.
|
|