Mécanique,
chute, oscillations mécaniques, portail.
Concours EMIA 2012.
école militaire interarmes
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Exercice
1
: Chute ( 2 / 7).
Un objet P 1
est lâché du haut d'une falaise ( point O) sans vitesse initiale. Un
second objet P 2 est lancé depuis le
point O avec une vitesse initiale horizontale v 0.
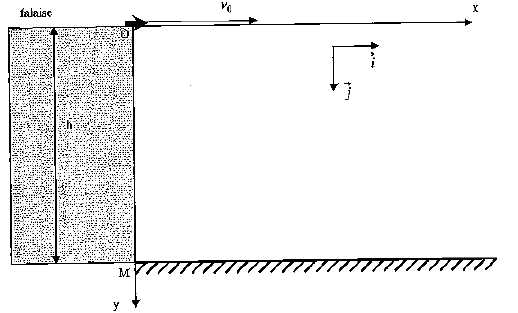
On admettra les hypothèses suivantes :
Les objets sont assimilés à des points matériels ; on néglige
les actions de l'air ; la falaise a une hauteur h = 10 m ; le mouvement
a lieu dans le plan vertical ( Ox, Oy ) ; g = 9,8 m s -2.
1.1. Enoncer la
deuxième loi de Newton.
Dans
un référentiel galiléen, la somme vectorielle des forces extérieures
appliquées à un solide est égale au produit de la masse M du solide par
l'accélération de son centre d'inertie.
1.2. L'objet P1
effectue-t-il un mouvement de chute kibre ? Justifier.
La résistance de l'air est négligeable. Cet objet n'est soumis qu'à son
poids. C'est une chute libre.
1.3. Même question
pour l'objet P2.
La résistance de l'air est négligeable. Cet
objet n'est soumis qu'à son poids. C'est une chute libre.
1.4. Etablir
les équations littérales x 2(t) et y 2(t)
de l'objet P 2 dans le repère choisi.
Accélération a x = 0 ; a y
= g.
Vitesse : v x = v 0 ; v y
= gt.
Position
x2(t) = v0t ; y2(t)
= ½gt2.
1.5. En déduire l'expression littérale de la
durée t2 de chute de P2.
h = ½gt22 ; t2
=(2h / g)½.
1.6. Lequel des deux
objets touchera le sol en premier ?
Accélération ax = 0 ; ay = g.
Vitesse de P1
: vx = 0 ; vy = gt.
Position
de l'objet P1 :x1(t) = 0
; y1(t) = ½gt2.
Les deux objets arrivent en même temps au sol.
|
|
|
Au cours d'une
deuxième expérience, un objet P3 de même masse M
est propulsé à l'aide d'un dispositif lanceur. Il coulisse dans une
glissière AO en subissant une force horizontale constante F3
qui s'exerce tant que l'ojet est dans la glissière, c'est à dire sur la
distance AO = L = 1 m.
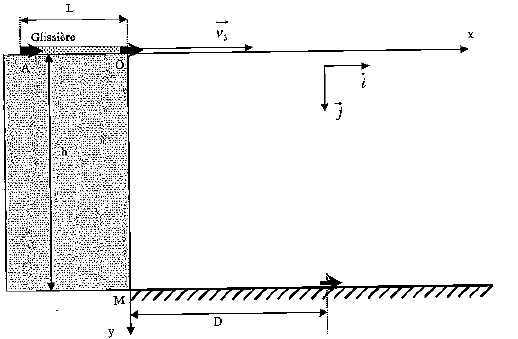
On néglige toutes les forces de frottement agissant sur l'objet et on
repère sa position lorsqu'il atteint le sol par la distance D3
par rapport au pied de la falaise.
1.7.
En utilisant les résultats précédents, démonter la relation suivante D3
= v3 (2h/g)½ où v3
est la vitesse de l'objet en O.
t3 =(2h / g)½
; D3 = v3t3
=v3
(2h/g)½ .
1.8. Faire le bilan
des forces appliquées entre A et O et les représenter sur un schéma.
Poids P, action normale du support et force propulsive F3.
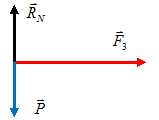
1.9. En appliquant
le théorème de l'énergie cinétique, déterminer l'expression de v3
en fonction de F3, M et L.
P et RN, perpendiculaires à la vitesse, ne
travaille pas.
Travail moteur de F3 : W = F3
L.
Variation de l'énergie cinétique : ½Mv32
= F3L ; v3 = (2F3L
/ M)½.
1.10. En déduire
l'expression de F3 en fonction de D3,
M, L, g et h.
D3 = v3 (2h/g)½
= (2F3L / M)½ (2h/g)½ ;
F3 = D32
Mg / (4Lh).
Lors d'un tir d'un quatrième objet P4, le
lanceur est réglé pour une force F4 quatre fois
plus intense que F3.
1.11.
Quelle est la relation entre les distances D4 et
D3 ?
F3
= D32 Mg / (4Lh) ; F4
= D42 Mg / (4Lh).
F3 / F4= (D3 / D4)2 = 0,25
; D3 / D4 = 0,5.
|
|
|
|
2. Oscillations mécaniques ( 2 /
7).
Oscillations
libres.
On considère un oscillateur mécanique qui est constitué d'un ressort
vertical idéal, de constante de raideur k et de longueur à vide L0
= 50,0 cm auquel est suspendu un solide S de
masse m = 100 g de centre G. L'ensemble est suspendu à une poutre fixe.
2.1. Représenter sur
un schéma le ressort à l'équilibre ainsi que le solide S en faisant
apparaître les forces agissant sur le solide S.
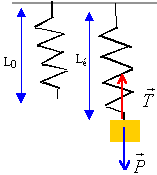
La masse m est soumise à son poids et à la tension
du ressort.
A l'équilibre ces deux forces sont opposées.
A l'équilibre : mg = k(Lé-L0).
2.2.
A l'équilibre Léq = 60,0 cm. Déterminer la
valeur littérale puis la valeur numérique de la constante de raideur k
du ressort..
k = mg / (Lé-L0)
= 0,100*9,8 / ( 0,600-0,500) = 9,8 N m-1.
Un opérateur écarte le solide S verticalement vers le bas et
l'abandonne sans vitesse initiale. Au moment où l'opérateur lâche le
solide S, la longueur du ressort est Lop = 69,0
cm. On appelle x(t) l'allongement algébrique du ressort, c'est à dire
la différence entre la longueur du ressort à l'instant t et la longueur
à l'équilibre. On suppose que le solide n'est soumis à aucun frottement.
3.3. Préciser les
caractéristiques du repère vertical dans lequel x(t) est également
l'abscisse du centre G du solide.
Origine : la position d'équilibre ; axe vertical orienté vers le bas.
3.4.
Etablir l'équation différentielle en x(t) du mouvement de G.
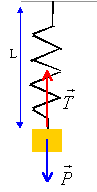
écarté de sa position d'équilibre le ressort
oscille : L= Léq +x.
mg-k(L-l0)= m d²x/dt² ;
mg-k( Léq +x-l0)=
m d²x/dt² ;
mg-k( Léq -l0)
- kx =m d²x/dt² ; or mg = k(Léq-L0)
m
d²x/dt² + k x=0 (1).
2.5.
En déduire
l'équation horaire du mouvement du solide.
x(t) = Xm
cos ( w0t)
avec w02
= k / m.
2.6.
Quelle est la
valeur de l'amplitude Xm ?
Xm = 69,0 -60,0 = 9,00 cm.
2.7. Déterminer
l'expression littérale de la période propre T0
du mouvement.
w0
= 2 p
/ T0 ; T0 = 2p( m/k)½.
2.8.
Calculer T0.
T0 =2*3,14 (0,100 / 9,8)½
=0,634 ~0,63 s.
2.9.
En réalité le solide S subit une action de frottement fluide. Si le
frottement est faible,quel est le type de mouvement observé ?
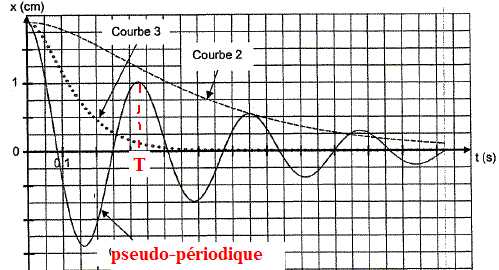
Mouvement pseudo-périodique.
2.10.
Pour un frottement faible, tracer l'allure du graphe x(t) en faisant
apparaître la pseudo-période T de l'oscillateur.
Oscillations
forcées.
L'oscillateur mécanique précédent est accroché à la membrane d'un haut
parleur alimenté par un générateur basse fréquence amplifié. La
membrane est alors animée d'un mouvement vertical sinusoïdal dont la
fréquence f est celle choisie sur le GBF. On constate qu'en faisant
varier la fréquence f, l'amplitude des oscillations du solide S varie
également.
2.11.
Identifier l'excitateur et le résonateur.
Excitateur : membrane du hautparleur ; résonateur : système solide S
ressort.
2.12.
Pour quelle valeur de f, l'amplitude des oscillations du solide
est-elle maximale ?
La fréquence f doit être égale à la fréquence propre du résonateur. f0
= 1 /T0 =1 / 0,634 ~ 1,6 Hz.
2.13.
Comment appelle-t-on ce phénomène ?
Résonance.
2.14.
Que se passe-t-il pour l'amplitude des oscillations lorsque la
fréquence f devient très grande ?
Du fait de l'inertie du système solide S ressort, l'amplitude des
oscillations est nulle.
|
Portail. ( 2 / 7).
La résolution sera essentiellement graphique.
La manoeuvre automatique d'un portail est réalisée grâce à un mécanisme
schématisé ci-dessous représenté dans différentes positions. Le portail
OF tourne autour de O. Le mécanisme moteur entraîne le bras O'A en
rotation autour de O', à l'extrémité de ce bras la bielette AB,
articulée en A et B transmet le mouvement au portail OB.
Le bras O'A, de longueur d = 40 cm, est moteur et sa vitesse de
rotation est égale à N = 3/p tr
/min par rapport au repère fixe. OF = 2,00 m.
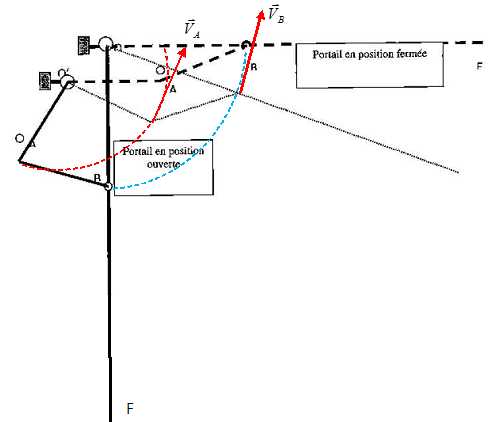
3.1.
Déterminer et placer le vecteur vitesse VA du
point A par rapport au repère fixe R0. Echelle 1
cm --> 0,01 m/s.
Vitesse angulaire w
= 2 p
N / 60 = 0,010 rad /s.
VA = w / d
= 0,010 / 0,40 = 0,025 m/s.
3.2. Déterminer la
direction et placer le vecteur vitesse VB du
point B par rapport au repère fixe R0 puis le
construire graphiquement.
Graphiquement O'A = AB ; VA =VB.
3.3.
En déduire la vitesse du point Fpar rapport au repère fixe.
Graphiquement OB
=3,5 cm et OF = 9,5 cm.
VB OB =VF OF ; VF
=0,025 *3,5 / 9,5 ~9,2 10-3 m/s. |
|