Mécanique du solide, pompe à pétrole, gravitation . Concours EMIA 2016.
école militaire interarmes

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.



. .



.
.


Exercice 1 : Pompe à pétrole.

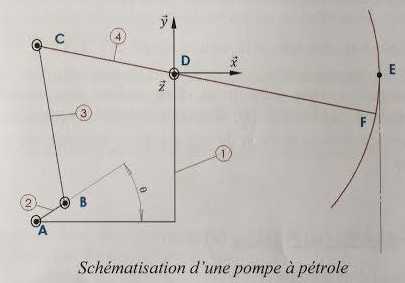
La pièce 1 forme le bâti fixe qui porte notament l'articulation D de la tête de cheval 4. La tête de cheval 4  est commandée par une bielle 3 articulée en C, elle même manoeuvrée par la manivelle 2 articulée en B. Cette manivelle est entraînée en rotation autour de l'axe ( A z ) par rapport au bâti 1 par un moteur non représenté ici. La rotation de la manivelle par rapport au bâti est repérée par l'angle q.
Le mouvement de va et vient vertical du câble est fourni par les oscillations de la tête de cheval en rotation autour de l'axe ( D z ). Un piston est accroché au bout du câble en E. Ce piston coulisse dans un cylindre assurant la fonction de pompage.
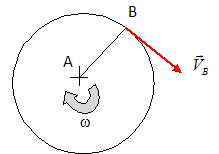
1. Sachant que la manivelle tourne dans le sens rétrograde ( antitrigonométrique ) à la vitesse angulaire uniforme N= 15 tr / min, calculer et tracer la vitesse  VB.
VB = w / AB avec w = 2pN/60 =2*3,14 *15 / 60 =  1,57 rad/s.

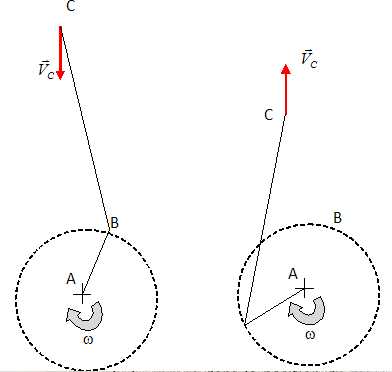
2. Esquisser la trajectoire du point C dans son mouvement par rapport  à 1.
Le point C est animé d'un mouvement de va et vient vertical.
3. En déduire et tracer la direction de la vitesse VC.

4. Construire par équiprolectivité du champ des vitesses, la vitesse du point C par rapport au bâti.
VC CD =VF DF.
5. Tracer le vecteur vitesse VE.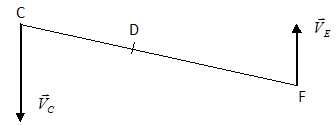

6. Sachant que le piston solidaire du câble coulise dans un cylindre dont l'alésage a un diamètre D = 100 mm, déduire le débit volumique instantané de la pompe.
Débit volumique ( m3 /s) = section du piston ( m2) * vitesse du point E ( m /s) = pD2/4 VE.




Analogies en physique ( 6 / 20).
Lancement d'un satellite.
Décollage, choix du site de lancement.
1. Définir les référentiels terrestre RT et géocentrique RG.
Le référentiel héliocentrique a pour origine le Soleil et des axes pointant vers des étoiles lointaines qui paraissent fixes.
Le référentiel géocentrique a pour origine le centre de la Terre et des axes parallèles à ceux du référentiel héliocentrique.
Un référentiel terrestre est un objet situé à la surface de la terre  par rapport auquel on se repère pour l'étude du mouvement d'un système ; on lui associe un repère et une origine des temps.
La terre est assimilée à une sphère de rayon R = 6371 km animée d'un mouvement de rotation uniforme autour de son axe Sud-Nord à la vitesse ngulaire W telle que la période de rotation sur elle même soit T = 23 h 56 min 4 s. On note l la latitude du point B représentant la base de lancement.


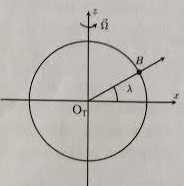
2. Donner la nature de la trajectoire d'un point B de la surface de la terre situé à la latitude l dans le repère RG.
Mouvement circulaire uniforme autour de l'axe Oz à la vitesse angulaire W.
 3. Donner l'expression du module de la vitesse de ce point B dans le repère RG.
V = W R cos l.
Calculer cette vitesse pour la base de lancement de Cap Canavral l1 = 28,5° et la base de Kourou l2 = 5,2°. W = 2 p / T = 2*3,14 / (23*3600+56*60+4)~7,3 10-5 rad/s.
Vcap = 7,3 10-5 *6,371 106 *cos 28,5 ~4,1 102 m/s.
VKou = 7,3 10-5 *6,371 106 *cos 5,4 ~4,6 102 m/s.
Une fusée de masse M décolle du point B, sans vitesse initiale par rapport à la terre, pour atteindre une orbite circulaire autour de la terre avec la vitesse finale V0 par rapport à RG.
4. Donner l'expression de la variation d'énergie cinétique de la fusée, en fonction de la vitesse de B, de V0 et M entre le moment de son décollage et l'arrivée sur son orbite.
On suppose que M rest constante.
DEc = ½MV02 - ½MVB2.
5. Calculer numériquement l'économie relative réalisée définie par :
(DEc1 -DEc2 ) / DEc1  avec l'indice 1 pour Kourou et 2 pour Cap Canaveral. V0 = 8 km /s.
DEc1 = ½MV02 - ½MVKou2.
DEc2 = ½MV02 - ½MVCap2.
(DE1 -DE2 ) = ½MVCap2 -½MVKou2.
(DEc1 -DEc2 ) / DEc1   =(VCap2 -VKou2) / (V02 - ½MVKou2).
(0,412 - 0,462) / (82 -0,462) = - 7 10-4.
La base de Kourou permet une économie d'énergie.
6. Pour quel autre type de lancement la base de Kourou est-elle avantageuse ?
La base de Kourou est proche de l'équateur. Elle est avantageuse pour le lancement de satellite géostationnaire.









Mise en orbite circulaire autour de la terre.
 7. Rappeler l'expression de la force gravitatioelle exercée par une masse ponctuelle mA située en A et une masse ponctuelle mB située en B. Faire un schéma.

Deux corps A et B de masses respectives mA et mB séparés d'une distance d=AB exercent l'un sur l'autre des forces opposées attractives, importantes dans l'infiniment grand, négligeables dans l'infiniment petit.

 


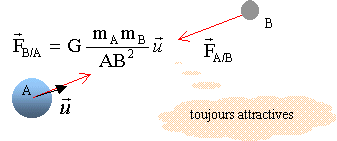
8. Rappeler l'expression de la force électrique exercée par une charge ponctuelle qA positive située en A sur une charge positive qB située en B. Faire un schéma.

Deux corps A et B de charges respectives qA et qB séparés d'une distance d exercent l'un sur l'autre des forces opposées attractives ou répulsives, importantes dans l'infiniment petit, négligeables dans l'infiniment grand.

 

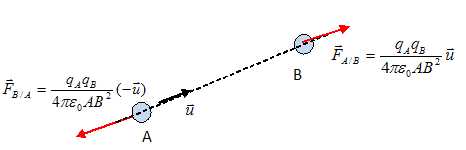
9. Rappeler l'énoncé du théorème de Gauss de l'électrostatique donnant l'expression du flux du champ électrostatique créé par une distribution de charge volumique r.

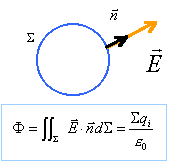
D'après le théorème de Gauss, le flux du vecteur champ électrique à travers la surface S est  égal à la somme des charges situées à l'intérieur de S divisée par e0. Ici qi = 4/3 pr3r. 

10. Par analogie énoncer le théorème de Gauss gravitationnel, donnant l'expression du flux du champ gravitationnel créé par une distribution de masse volumique µ0. Quelle expression est analogue à e0 ?

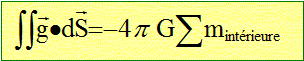  Ici mi = 4/3 pr3µ0.
L'expression - 1 /(4pG) est analogue à e0.

 
La terre est de nouveau assimilée à une boule à symétrie sphérique de centre O et de masse M = 5,97 1024 kg.
11. Quelle est la direction du champ gravitationnel  terrestre ? Justifier.
Ce champ est toujours dirigé vers le centre de la terre, les forces de gravitation sont toujours attractives.
12. Déterminer ce champ en tout point extérieur de la terre. Quelle est sa valeur à la surface de la terre ?

On choisit comme surface S est une sphère de rayon r : S = 4pr2.

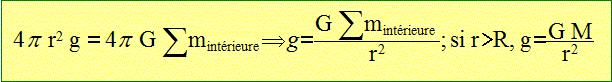
A la surface de la terre g0 = GM/R2, avec R, rayon terrestre.

13. Retrouver alors l'expression de la force associée à ce champ de gravitation exercée par la terre sur un satellite de masse m situé en orbite circulaire de rayon r.
F = m g = GmM / r2.
14. Déduire de l'expression de cette force, le potentiel associé créé en P. C'est ube énergie potentielle, supposée nulle à l'infini.

Le champ de gravitation dérive d'un potentiel scalaire V :( ce potentiel est nul à l'infini )

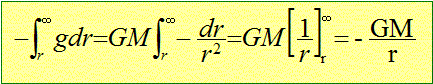
15. Enoncer la seconde loi de Newton. 
Dans un référentiel galiléen, la somme vectorielle des forces extérieures appliquées à un solide est égale au produit de la masse M du solide par l'accélération de son centre d'inertie.
16. Appliquer cette loi au satellite de masse m, dans le repère de Frenet, sachant qu'il décrit une orbite circulaire autour de la terre à la vitesse v0.
Le satellite est soumis à la seule force attractive centripète exercée par la terre. Suivant l'axe dirigé vers le centre de la terre, la seconde loi de Newton s'écrit : 
GMm / r2 = maN = m v02 / r soit v02 = GM / r.
17. En déduire l'énergie cinétique du satellite.
Ec = ½mv02 = ½GMm / r.
18. On note T la période de révolution du satellite. Exprimer le rapport liant cette période à la distance r entre le satellite et le centre de la terre T2 / r3. Comment se nomme cette loi ?
Le satellite décrit la circonférence 2pr à la vitesse v0 pendant la durée T.
2pr = v0 T ; 4 p2r2 = v02T2 = GM / r T2 ;   T2 / r3 = 4 p2/ (GM). 3è loi de Kepler.
19. Calculer la vitesse v0 et la période T d'un satellite Helios 2 sur une orbite circulaire basse à l'altitude de 675 km.
4 p2/ (GM) = 4 *3,142 / (6,67 10-11 * 5,97 1024) =9,91 10-14.
r = 6371 +675 = 7046 km = 7,046 106 m.
T2 = 9,91 10-14( 7,046 106 )3 =3,47 107 ; T = 5,89 103 s ~1 h 38 min.
20. Que savez-vous des satellites Hélios 2 ( Répondre en une phrase ).
Leur orbite étant polaire, ce sont des satellites de reconnaissance en particulier du bloc soviétique.

  .

 


  

menu