Carbone
14, la houle, magnétostatique.
Concours EMIA 2016.
école militaire interarmes
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Exercice
1
: datation au carbone 14 ( 3 / 20).
Le carbone 14 ( 146C)
est radioactif est radioactif et se désintègre en émettant une
particule ß -.
1.
Ecrire l'équation bilan de cette réaction nucléaire. Quelle(s) loi(s)
de conservation utilisez-vous ?
146C
---> 147N
+ 0-1e.
Conservation
de la charge et conservation du nombre de nucléons.
On rappelle que le nombre N de noyaux radioactifs d'une source
radioactive diminue au cours du temps selon la loi de décroissance :
N = N0 exp(-lt) où
l
est la constante radioactive de ce nucléide.
2.
Donner la composition en protons et neutrons du noyau de carbone 14 et
de son isotope le plus connu.
146C
: 6 protons et 14-6 = 8 neutrons ; 126C
: 6 protons et 12-6 = 6 neutrons.
3. Rappeler la
définition de la période radioactive.
La demi-vie radioactive,(ou
période) notée t½, d'un échantillon de noyaux radioactifs est égale à
la durée au bout de laquelle la moitié des noyaux radioactifs initiaux
se sont désintègrés.
La période
radioactive du carbone 14 est T = 5700 ans.
4. Retrouver la
relation qui lie cette période à la constante radioactive
N(t½) = ½N0 = N0
exp(-lt½) ; 0,5 =exp(-lt½) ; ln0,5 = -ln2 = -lt½ : ln2
= lt½.
5.
Tracer l'allure de la courbe de décroissance
radioactive.
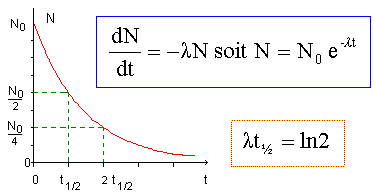 6.
Expliquer grâce
à votre courbe comment on détermine l'âge d'un échantillon.
6.
Expliquer grâce
à votre courbe comment on détermine l'âge d'un échantillon.
La
teneur en carbone 14 est constante dans le monde ( dans l'atmosphère
comme dans chaque organisme vivant ). Cela est du à un équilibre entre
la désintégration et la production de carbone 14. Chaque gramme de
carbone contient des atomes de carbone 14. On enregistre en moyenne
13,5 désintégrations par minute et par gramme de carbone. Lorsqu'un
arbre, par exemple, est abattu, le bois cesse de vivre, le processus de
photosynthèse s'arrête et il n'y a plus d'absorption de dioxyde de
carbone. Le carbone 14 est alors libre de se désintégrer sans
compensation. On peut donc dater l'âge de la mort de l'organisme ( au
moment où cesse tout échange de CO2 avec
l'atmosphère).
Le prélèvement d'une poutre en bois dans une tombe au Sahara fournit
une activité au moment de la mesure telle que A= 6,68 désintégrations
par minute et par gramme de carbone alors que A0 = 13,5
désintégrations par minute et par gramme de carbone.
On passe ensuite de l'activité au nombre de noyaux N(t) à l'aide de la
relation N(t) = A / l
.
A(t) /A0 = exp (-lt) ; ln [A(t) /A0 ] = -lt ; ln [A0/A(t) ] =lt ;
ln [A0/A(t)
] = t ln2 / t½ ; t = t½ / ln 2
* ln(A0/A)
On estime possible de dater des échantillons jusqu'à 51300 ans.
7. Pourquoi
n'est-ilpas possible d'aller au-delà ? Justifier par un calcul .
t / t ½ = ln [A0/A(t) ]
/ ln 2 = 51300 / 5700 = 9.
ln [A0/A(t)
] = 9 ln2 = 6,23 ; A0/A(t)
=512 ; A(t) ~2 10-3 A0.
Au delà de 51300 ans l'activité résiduelle de l'échantillon est devenue
trop faible pour être mesurée avec précision.
|
|
|
Physique des ondes :la houle ( 2
/ 20).
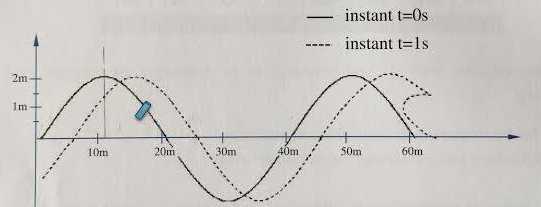
1.
Définir ce qu'est une onde mécanique progressive. La houle est-elle une
onde longitudinale ou transversale ?
Une onde mécanique progressive est la propagation d'une perturbation
dans un milieu matériel avec transport d'énergie, sans transport de
matière.
La direction de
déformation du milieu est perpendiculaire à la direction de
propagation. La houle est une onde transversale.
Quelle sera la position du morceau de bois au bout d'une seconde ?
Le bout de bois monte verticalement ( environ jusqu'à 1,8 m )
sans se déplacer horizontalement.
2. A l'aide de la
figure déterminer la célérité de cette onde ; définir la longueur
d'onde et la déterminer ; définir la période et la déterminer.
En une seconde,le front de l'onde avance de 5 m. Célérité c = 5 m /s.
La longueur d'onde est la distance parcourue par le front de l'onde en
une période ( distance entre deux maximas successifs l ~ 40
m ).
La période temporelle est égale à la longueur d'onde divisée par la
célérité soit T = 40 / 5 = 8 s.
3. Une série de
mesures expérimentales a permis de montrer que le carré de la célérité
de l'onde est proportionnel à la longueur d'onde. Quelle est la
dimension du coefficient de proportionnalité ?
c2 = k l ; k
= c2 / l.
c2 s'exprime en m2 s-2
et l
s'exprime en mètre.
k s'exprime en m s-2.
|
|
|
|
Magnétostatique ( ~ 4 /20).
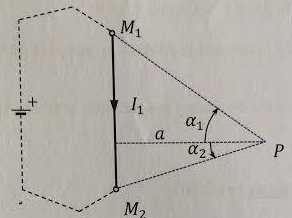
Le circuit est parcouru par un courant d'intensité I1 et placé dans le vide de perméabilité µ0.
Ce circuit comporte, en plus d'éléments supposés infiniment éloignés
dont la contribution au champ magnétique B sera négligée ( en
pointillés sur le schéma ), un tronçon filiforme et rectiligne M1M2. L'intensité I1 est comptée positive dans le sens M1 --> M2.
1. Démontrer que le circuit apporte en P, situé à une distance a, une contribution B au champ magnétique de norme :
B = µ0 I1 /(4 p a) ( sin a2-sin a1).
Préciser le sens et la direction de B.
On considère un segment de fil de longueur L, parcouru par un courant I.
L'élément
de courant Idl crée en P un champ magnétique élémentaire dB,
perpendiculaire au plan formé par Idl et MP, orienté vers l'avant du
plan.
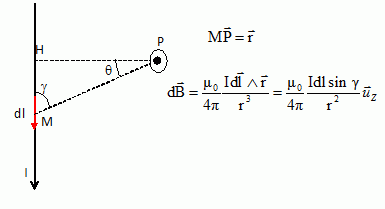
tan q = MH /HP ; MH = HP tan q ; dériver dMH = dl = HP dq / cos2q.
De plus : sin g = cos q, et r = HP / cos q, d'où :
dl sin g / r2 = HP cos q dq .
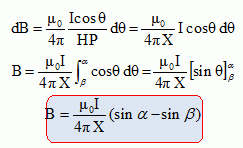 avecX = a, a =a2 et ß = a1. avecX = a, a =a2 et ß = a1.
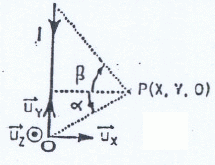
2. On étudie maintenant le tronçon ci-dessous :
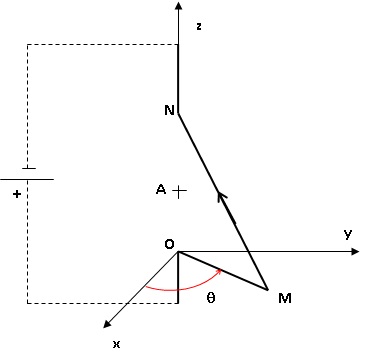
OM = ON = L ; OA = AN ; le tronçon étudié comporte, en plus
d'élémentssupposés infiniment éloignés dont la contribution au champ
magnétique sera négligée ( en pointillés sur le schéma, un conducteur
filiforme parcouru par un courant d'intensité I.
Exprimer les composantes du champ magnétique créé en A ( 0,0 ,½L).
Les deux parties verticales du circuit créées en A un champ magnétique
nul car en chaque point P de ces ces portions de circuit, les
vecteurs Idl et PA sont colinéaires.
Champ magnétique créé par OM en A.
Ce champ est perpendiculaire au plan formé par (OM) et (AN), dirigé vers l'avant du plan.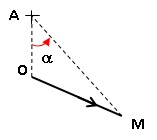
On applique le résultat précédent A jouant le rôle de P, O le rôle de M1 et M le rôle de M2.
alors X = HP = OA ; b = 0 et tan a = OM / OA = 2.
Champ magnétique créé par MN en A.
Ce champ est perpendiculaire au plan formé par (MN) et (AN), dirigé vers l'avant du plan.
On applique le résultat précédent avec A jouant le rôle de P, M le rôle de M1 et N le rôle de M2.
a = 45° ; cos a = AH / AN = 2 AH / L ; tan g = OA / OM = 0,5 ; AM = OA / sin g et cos ß = AH / AM .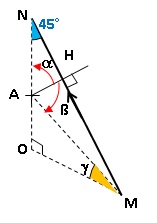
|
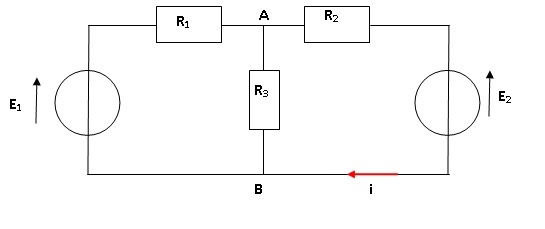
Electronique ( 2 pts).
.
1. Rappeler la
forme générale du théorème de Thévenin équivalent à un dipôle linéaire
quelconque, en rappelant la définition des paramètres de ce générateur
équivalent.
Un dipole actif linéaire peut être modélisé par une source de tension parfaite associée en série avec une résistance Rth.
2. Déterminer la schéma de Thévenin pour le dipôle AB constitué de E1, R1 et R3.
R1 et R3 en série : Rth = R1+R3 = 150 ohms ; Eth = E1 = 5 V.
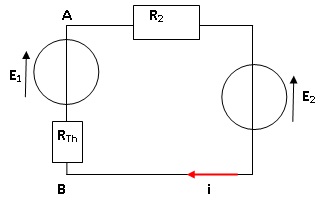
i = (E1-E2) / (RTh+R2 )= 0.
3. En déduire l'intensité i.
R1=R2 = 2R3 = 100 ohms et E1 =E2 = 5 V.
On remplace les générateurs de Thévenin (E1 ; R1 ) et (E2 ; R2) par les deux générateurs équivalents de Norton, puis les générateurs de Norton par un générateur unique de Norton.
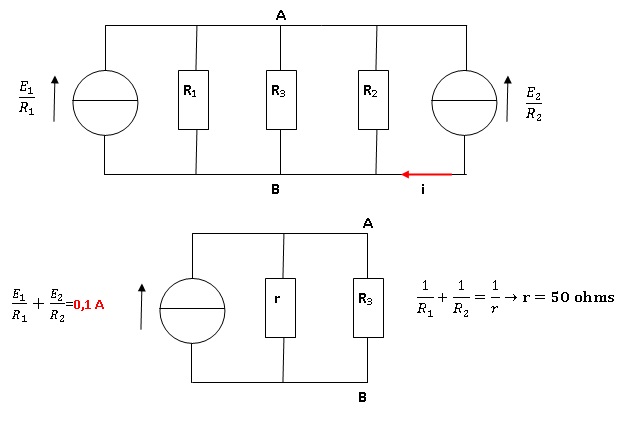
|
|