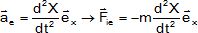Etude d'un sismographe. Concours EMIA 2013. école militaire interarmes En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Partie A : étude du système masse ressort. On considère un ressort vertical à spires non jointives supposé parfait. Il est caractérisé par une constante de raideur k. Un solide S de centre d'inertie G et de masse m, est accroché à son extrémité inférieure. L'étude est faite dans le référentiel du laboratoire supposé galiléen. L'axe Ox est vertical dirigé vers le bas, le point origine O correspondant à la position d'équilibre du point G. On note : L0 : longueur du ressort à vide ; Léq : longueur du ressort à l'équilibre quand le solide S est suspendu et immobile ; L(t) : longueur du ressort à un instant t pendant le mouvement vertical du solide S ; x(t) = L(t)-Léq : position du centre d'inertie G du solide S par rapport à la position d'équilibre. m = 10,0 kg ; k = 0,440 N m-1.  1.1. Faire un bilan des forces appliquées au solide S lorsqu'il est à l'équilibre. 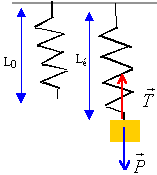à l'équilibre : mg = k(Léq-L0) ; Léq = mg / k +L0. 1.2. Même question pour une position quelconque du solide S.  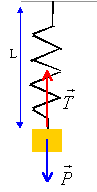1.3. Enoncer la seconde loi de Newton. Dans un référentiel galiléen, la somme vectorielle des forces extérieures appliquées à un solide est égale au produit de la masse M du solide par l'accélération de son centre d'inertie.   1.4.  En déduire l'équation différentielle vérifiée par la variable x(t). mg-k(L-L0)= m d²x/dt² mg-k( Léq +x-L0)= m d²x/dt² mg-k( Léq -L0) - kx =m d²x/dt² ; or mg = k(Léq-L0) m d²x/dt² + k x=0  ; d²x/dt² + k / m x=0(1) 1.5. Résoudre cette équation pour les conditions initiales suivantes x(t=0)=x0 et vitesse initiale nulle. On pose w02 = k/m ; x(t) = A cos (w0t +B) avec A et B des constantes. x(t=0)=A cos B = x0 soit A = x0 et B = 0. x(t) = x0 cos (w0t ). 1.6. Déterminer l'expression littérale de la période T0 de cet oscillateur. T0 = 2p / w0 = 2p [m / k]½. 1.7. Faire l'application numérique pour T0. T0 = 2*3,14 [10,0 / 0,440]½ =29,95 ~30,0 s. 1.8. Quelle est l'énergie potentielle totale du solide S. La référence est la position d'équilibre du solide S. Ep = ½kx2. 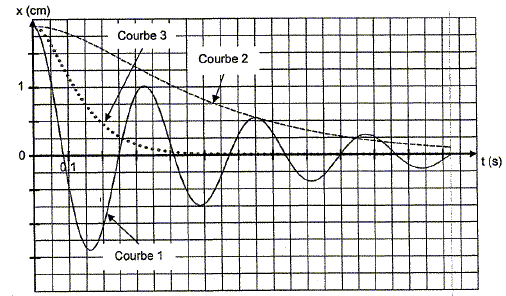1.9 Calculer l'énergie mécanique du solide S dans les conditions initiales décrites et commentez le résultat obtenu. La vitesse initiale étant nulle, l'énergie mécanique du solide S est sous forme potentielle : EM =½kx02. Partie B. Etude du système masse ressort amortisseur.  On considère le même système que précédemment auquel on a ajouté en série un système amortisseur par une foce de frottement fluide de norme f = k' v où k' est une constante positive et v la vitesse du centre d'inertie du solide S. 2.1. Etablir la nouvelle équation différentielle du mouvement. Ecrire la seconde loi de newton sur un axe vertical dirigé vers le bas ; l'origine de l'axe est la position d'équilibre stable du système masse ressort : L= Léq +x mg-k(L-l0)-k' v= m d²x/dt² mg-k( Léq +x-l0)-k' v= m d²x/dt² mg-k( Léq -l0) - kx -k' v =m d²x/dt² ; or mg = k(Léq-L0) m d²x/dt² +k' v + k x=0 avec v = dx/dt = x' m d²x/dt² +k' x' + k x=0 (2) 2.2 Cette équation est formellement identique à celle obtenue  lors de l'étude d'oscillations électriques dans un circuit. De quel circuit électrique s'agit-il ? Circuit RLC série. 2.3. Si le frottement est faible, quel sera le type de mouvement observé ? Mouvement pseudo-périodique .  2.4. Tracer l'allure du graphe x(t). Quels sont les deux autres régimes d'ozcillations que l'on peut observer en augmentant le frottement ? Courbe 1 : régime pseudo-périodique ; courbe 2 : régime critique ; courbe 3  régime apériodique. Partie C. Un sismographe simple. Le système étudié à la partie B est fixé à l'intérieur d'un boîtier en contac avec le sol. Le solide S est solidaire d'un stylet qui inscrit les mouvements sur un papier placé sur un cylindre en rotation et fixé au boîtier solidaire du sol. Lors du passage d'une onde sismique, on considère que le sol et donc le boîtier sont animés d'un mouvement sinusoïdal vertical. On repère la position du boîter à partir de sa position au repos, par son abscisse X(t)=A sin (wt) compté positivement vers le bas. 3.1. Identifier l'excitateur et le résonateur. L'excitateur et l'onde sismique et le résonateur le système masse ressort amortisseur. 3.2. Expliquer pourquoi le référentiel du laboratoire qui est donc lié au sol et au boîtier que l'on notera Rboitier ne peut pas être considéré comme galiléen lors du passage d'une onde sismique. Lors du passage de l'onde sismique, le référentier Rboitier n'est pas animé d'un mouvement rectiligne uniforme par rapport à un référentiel galiléen. On distinguera donc dorénavant le référentiel galiléen lié au sol immobile Rg et le référentiel lié au boîtier. 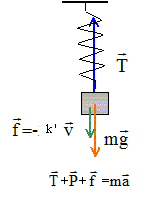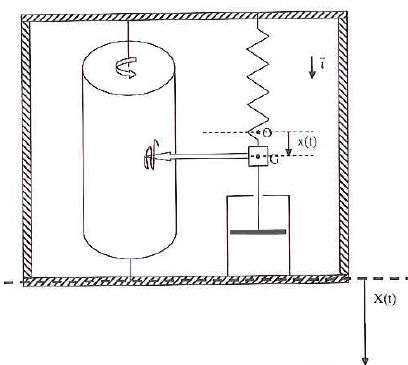La deuxième loi de Newton doit dans ce cas être modifiée par la prise en compte d'une nouvelle force d'inertie d'entraînement ou ae est l'accélération d'entraînement. 3.3. Déterminer l'expression de l'accélération d'entraînement puis la force Fie. Dans le référentiel non galiléen Rboitier, en translation par rapport au référentiel galiléen Rg, le solide S est soumis à une force d'inertie : X(t) = A sin ( wt) ; dX(t) /dt = wA cos ( wt) ; d2X(t) /dt2 = -w2A cos ( wt). 3.4. En déduire la nouvelle équation différentielle du mouvement du solide S. Sa résolution n'est pas demandée. m d²x/dt² +k' x' + k x=mw2A cos ( wt). 3.5. Quand dit-on qu'i y a résonance ? Il y a résonance ( augmentation de l'amplitude d'oscillation d'un système physique) lorsque celui-ci est excité au voisinage de l'une de ses fréquences propres. 3.6. Dans le cas d'un amortissement faible, donner l'allure de la courbe de réponse en amplitude en fonction de la fréquence.   .

menu