Mathématiques.
Concours Aspts SUD EST 2016.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
1. Ecrire si possible sous la forme an.
A = 53 x 23 = 103.
B = (-3)5 x (-3)2 = (-3)7.
C= 158 / 58 =38 x 58 / 58 = 38.
D = 53 x 52x54 = 59.
Calculer X3 sous forme d'un produit de puissances pour X = 52 x74.
X3 = 56 x 712.
Donner l'écriture scientifique de Y2 pou Y = 1,2 10-3.
Y2 = 1,44 10-6.
2. Montrer que les nombres A et b sont égaux.
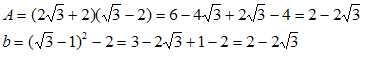
3. Compléter :
12 m/s = 12*3,6 km/h = 43,2 km/h.
110 km / h = 110 /3,6 m/s ~30,6 m / s.
420 tr / min = 420 / 60 tr /s = 7 tr/s.
700 kg m-3 = 0,7 g cm-3.
4,8 g cm-3 = 4,8 kg dm-3.
540 kg m-3 = 540 g dm-3.
4. Dans la série suivante, dire si les afirmations sont vraies ou fausses. Justifier.
Série : 4,5 ; 10,5 ; 16 ; 2,5 ; 10 ; 12 ; 2,5 ; 4,4 ; 5 ; 7,5 ; 7,5 ; 10.
ordonnons la série : 2,5 ; 2,5 ; 4,4 ; 4,5 ; 5 ; 7,5 ; 7,5 ; 10 ; 10 ; 10,5 ; 12 ; 16.
a. L'étendue est de 16, faux.
Plus grand nombre - plus petit nombre = 16-2,5 = 12,5.
b. La moyenne est 7, faux.
(2,5 +2,5 + 4,4 + 4,5 +5 +7,5 +7,5 +10 +10 +10,5 +12 +16) / 12 =7,7.
c. La médiane est 7,5, vrai.
La médiane partage une série en deux groupes de même effectif.
d. Le premier quartile est 4,5, faux..
Au moins 25 % des valeurs de la série sont inférieures ou égales au premier quartile, soit ici 4,4.
e. Le troisième quartile est 10,5, faux.
Au moins 75 % des valeurs de la série sont inférieures ou égales au troisième quartile, soit ici 10.
|
|
|
5.
On dispose de dix cartes qui sont les suivantes : 10 de coeur, sept de
coeur, as de carreau, valet de coeur, dame de trèfle, as de trèfle, roi
de carreau, dame de carreau, sept de pique et valet de pique.
On tire une carte au hasard. Quelle est la probabilité des événements suivants ?
a. Tirer l'as de trèfle. 1/10 = 0,10.
b. Tirer un as. 2 /10 = 0,20.
c.Tirer une carte rouge. 6 / 10 = 0,60.
d. Tirer une dame. 2 /10 = 0,20.
6. D = (3x-1)(2x+5) -(3x-1)2.
a. Développer et réduire l'expression.
b. Factotiser l'expression.
D =(3x-1) [2x+5-(3x-1)] =(3x-1)( -x+6).
D = -3x2+18x+x-6
D = - 3x2+19x-6.
|
|
|
|
7. Résoudre les équations suivantes.
(5-6b) (4b+11)-(3b+7)(5-6b)=0.
20b +55 -24b2 -66 b -(15 b -18b2+35-42 b)=0.
20b +55 -24b2 -66 b -15 b +18b2-35+42 b=0.
-6b2 -19b +20 = 0.
Discriminant D =(-19)2 -4*(-6)*20 =841 ; 841½ = 29.
Solutions b1 = [19 +29] / (-12) = -4 ; b2 = (19-29) /(-12) = 5 / 6.
(4b-2)(5b+1)-(1+5b)(2b-4)=0.
20b2+4b-10b-2 -(2b-4+10b2-20 b)=0
20b2+4b-10b-2 -2b+4-10b2+20 b=0
10b2+12b+2 = 0
5b2 +6b+1 =0.
Discriminant D =(6)2 -4*5 =16 ; 16½ = 4.
Solutions b1 = [-6 +4] / 10 = -0,2 ; b2 = (-6-4) /10 = -1.
8. Résoudre le système suivant :
5(x+y) +2,2 +x=10 et 3x-6(y+1)= -2x-12.
6x+5y=7,8 et 5x -6y= -6.
y = 1 +5 /6 x.
6x +5(1+5 /6 x) =7,8.
6x +25 / 6x = 2,8 ;
36x +25x = 2,8*6 = 16,8 soit x = 16,8 / 61 =168 / 610 =84 / 305 ~0,275.
Par suite y = 1 +5*84 /(6*310) =1 +7 /31 =38 / 31~1,225.
9. Soit
un carré. On augmente la longueur du côté de 4 cm. On obtient un
nouveau carré dont l'aire mesure 60 cm2 de plus que l'aire du carré
précédent. Quelle est la longueur du côté du premier carré ?
On note a le côté du carré.
(a+4)2 = a2+60.
a2 +8a+16 = a2+60.
8a = 44 ; a = 5,5 cm.
10. Une fonction affine f a une représentation graphique qui passe par les points G(-1 ; 7 ) et H (2 ; -2 ).
Déterminer l'expression algébrique de f.
f est de la forme y = a x + b avec a et b des constantes.
En G : 7 = -a +b ;
En H : -2 = 2a +b.
Soustraire : -2-7 = 2a+a ; a = -3 et b = 4.
f(x) = -3x+4.
11. Soit un triangle ACE tel que CE = 73 mm, AC = 48 mm et AE = 55 mm.
a. Ce triangle est-il rectangle ? Justifier.
732 = 5329 ; 482 +552 = 5329.
La relation de Pythagore étant vérifiée, ce triangle est rectangle en A.
b. Déterminer l'arrondi au degré près de l'angle AEC.
sin AEC = AC / CE = 48 / 73 = 0,6575 ; l'angle mesure environ 41°.
|
|