Concert et oreille
humaine.
Concours orthoptie Nantes 2016.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Un
ingénieur du son a un rôle primordial pour la sonorisation des salles,
en particulier lors d'un concert de musique. A l'aide d'une table de
mixage, il règle les sons qui arrivent depuis les microphones des
musiciens et les renvoie vers les enceintes de façade et de retour.
L'ingénieur intervient sur 4 paramètres des sons : la hauteur, l'intensité, le timbre et la durée.
Grâce à la table de mixage, il convertit facilement un son en un autre.
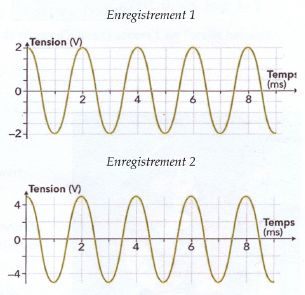
Il peut notamment modifier un son correspondant à l'enregistrement 1 en
un son correspondant à l'enregistrement 2.
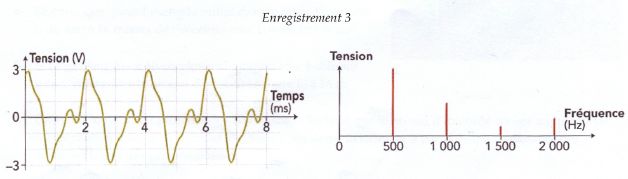
Les différentes représentations d'un son lui permettent de reconnaître ses caractéristiques ( voir enregistrement 3).
1.
Déterminer la fréquence du son correspondant à l'enregistrement 1.
Période T = 2,0 ms ; fréquence f = 1 / T = 1 / 0,0020 = 5,0 102 Hz.
2. Quelle modification a effectué l'ingénieur du son pour obtenir l'enregistrement 2 ?
L'amplitude a augmenté, la fréquence reste inchangée : l'ingénieur a augmenté l'intensité du son.
3.
En utilisant l'analyse spectrale, montrer que la hauteur du son émis
lors de l'enregistrement 3 est identique à celle des enregistrements 1
et 2..
Engestrement
3 : la fréquence du fondamental est égale à 500 Hz. La hauteur de ce
son est 500 Hz, donc identique à celle des enregistrements 1 et 2.
4. Quelle différence présente le son de l'enregistrement 3 par rapport aux enregistrements 1 et 2 ? Justifier.
Enregistrements 1 et 2 : on observe une sinusoïde, les sons sont purs.
Enregistrement 3 : on observe plusieurs harmoniques, le son est complexe.
5. Quel paramètre du son est ainsi mis en évidence ?.
Les sons 1, 2 et 3 n'ont pas le même timbre.
|
| .
. |
|
|
Pour
régler le niveau sonore de la salle de concert, l'ingénieur connaît
certaines règles. Par exemple, s'il fait ses réglages pour avoir un son
de 98 dB pour les spectateurs situés à 16 m d'une enceinte, il sait que
l'intensité sonore sera quatre fois plus grande pour les spectateurs
situés à 8 m de l'enceinte. Il sait aussi que l'intensité sonore double
s'il place côte à côte deux enceintes identiques. Pour ces réglages
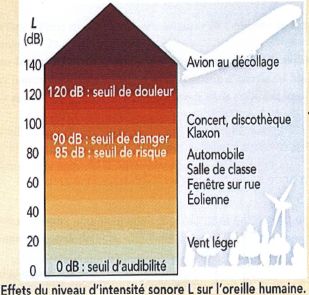
l'ingénieur doit tenir compte des seuils de risque, de danger et de
douleur. En effet l'exposition à un niveau sonore trop élevé peut
provoquer des acouphènes.
|
|
|
|
6. Montrer que l'intensité I1 du son à 16 m de l'enceinte vaut 6,3 10-3 W m-2.
I1 = I0 10L/10 =1,0 10-12* 109,8 = 1,0 10-2,2 = 6,3 10-3 W m-2.
7. Si l'ingénieur place 10 enceintes identiques côte à côte sur scène, déterminer le niveau sonore L2 à 16 m.
I2 = 10 I1 = 6,3 10-2 W m-2.
L2 = 10 log[I2 / I0]=10 log[6,3 10-2 / 10-12]~108 dB.
8.
On est toujours en présence de 10 enceintes. Sachant que le niveau
d'intensité sonore augmente de 6,0 dB chaque fois que l'on divise la
distance par 2, déterminer à partir de quelle distance des enceintes le
son devient douloureux.
Seuil de la douleur : 120 dB.
120 -108 = 12 dB ; en divisant la distance par quatre, on atteint le seuil de la douleur.
16 / 4 = 4,0 m.
|
|