Sondeur
à ultrasons, le fluor.
Concours orthoptie Rennes 2012.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Exercice 1. Le sondeur à ultrasons.
Sur
un bateau, un sondeur est un appareil servant à mesurer la profondeur
de la mer ( distance entre la surface et le fond de la mer ). Les
sondeurs sont généralement acoustiques : la profondeur est
déduite de la mesure du temps de trajet d'un signal acoustique réfléchi
par le fond. Le signal acoustique utilisé est une onde ultrasonore.
Quelques généralités sur les ondes.
1.
Définir une onde mécanique.
Une onde
progressivemécanique est la propagation d'une perturbation dans un milieu
matériel avec transport d'énergie, sans transport de matière.
2.
Les ultrasons sont-ils des ondes mécaniques ? Si oui, donner un exemple
d'onde non mécanique, si non à quel type d'onde appartiennent les
ultrasons ?
Une onde
ultrasonore est une onde mécanique progressive longitudinale.
La lumière est une onde électromagnétique.
3. L'onde ultrasonore est-elle longitudinale ou transversale ? Justifier.
Une onde
ultrasonore est une onde mécanique progressive longitudinale. La
propagation de la variation de pression a la même direction que l'onde.
4. Citer un fait expérimental qui permet de décrire les ultrasons comme une onde.
La diffraction.
Etude des ultrasons émis.
Le
sondeur émet des salves d'ultrasons à intervalles de temps régulier. On
étudie une salve d'ultrasons grâce à l'oscillogramme ci-dessous obtenu
à partir d'un capteur délivrant un signal lié aux ultrasons. Le
coefficient de balayage est de 10 µspar division.
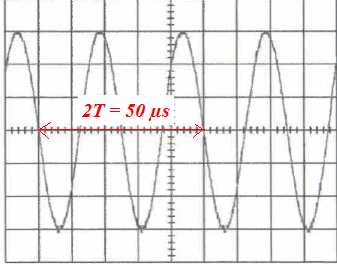
v = 0,03 Vson =0,03*340~10 m/s.
5. Déterminer la fréquence des ultrasons utilisés.
T = 25 µs = 2,5 10-5 s ; f = 1 / T = 1/(2,5 10-5)=40 kHz.
6. La célérité des ultrasons dans l'eau vaut v = 1,5 km/s. En déduire la longueur d'onde des ultrasons.
l = v / f = 1,5 103 / (4,0 104) =3,75 10-2 ~3,8 10-2 m.
7.
On suppose que l'eau n'est pas un milieu dispersif pour les ultrasons.
définir ce qu'est un milieu dispersif. En déduire la valeur de la
célérité des sons dans l'eau de mer.
Dans un milieu dispersif, la célérité de l'onde dépend de sa fréquence.
Célérité des sons dans l'eau de mer : v = 1,5 103 m/s.
8. Entre l'émission et la réception de la salve, il s'est écoulé une durée Dt = 32 ms. Quelle est la profondeur de la mer ?
Aller + retour = v Dt ; aller = retour = 0,5 v Dt =0,5 *1,5 103*32 10-3 = 24 m.
|
| .
. |
|
|
Etude du circuit d'émission des ultrasons.
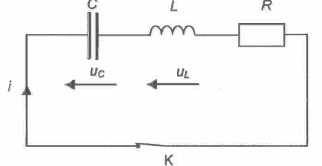
9. Etablir l'équation différentielle en uc de ce circuit.
Additivité des tensions : uc+uL+Ri = 0.
uL = Ldi/dt ; i = dq/dt = Cduc/dt ; di/dt = Cd2uc/dt2.
LCd2uc/dt2 +RCduc/dt +uc = 0.
d2uc/dt2 +R/L duc/dt +uc/ (LC) = 0.
10. On se place dans le cas
d'un amortissement négligeable : R=0. On suppose qu'à t=0, le
condensateur est chargé sous une tension U0.
Effectuer la résolution analytique de l'équation différentielle.
d2uc/dt2 +uc/ (LC) = 0. On pose w02 =1/( LC).
uc= A cos ( w0t +F) avec A et F des constantes déterminées par les conditions initiales.
uc(t=0) = U0 =A cos F ; F =0 et A = U0.
uc= U0 cos ( w0t).
En déduire l'intensité du courant i dans le circuit.
i = Cduc/dt = -CU0w0sin (w0t) = -[C/L]½U0sin (w0t).
Si L = 12 mH, quelle capacité C doi-on choisir ?
w0 =1/( LC)½ = 2 p f ; C = 1/(L4 p2f2) =1/(0,012*4*3,142*(4,0 104)2)=1,3 10-9 F.
11.
En réalité la résistance n'est jamais nulle. On la supposera assez
faible pour que les oscillations soient toujours réalisables dans le
circuit.
De quel type de régime de fonctionnement du circuit RLC s'agit-il ?
Régime pseudo-périodique.
Dans le cas d'amortissement faible tracer l'allure de la courbe représentant uc au cours du temps.
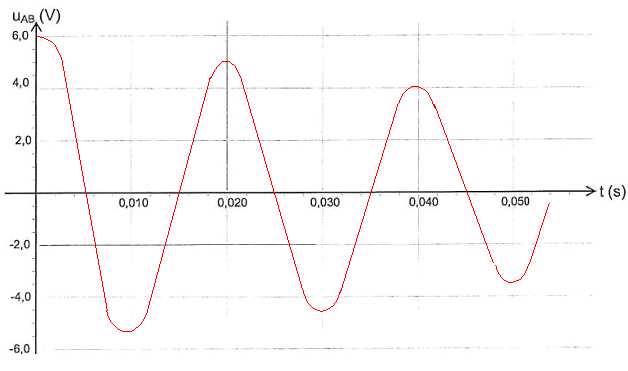
Expliquer en terme énergétiques les échanges d'énergie qui ont lieu lors de la première pseudo-période.
Au
cours des échanges d'énergie entre bobine et condensateur, une partie
de celle-ci est dissipée par effet Joule dans les parties résistives du
circuit.
Entre t=0 et t = 0,25 T : décharge du condensateur dans la bobine qui stocke de l'énergie.
Entre t = 0,25T et t = 0,5 T : charge en sens contraire du condensateur, la bobine libère son énergie.
Entre t=0,5 T et t = 0,75 T : décharge du condensateur dans la bobine qui stocke de l'énergie.
Entre t = 0,75T et t = T : charge en sens contraire du condensateur, la bobine libère son énergie.
|
|
|
|
Exercice 2. Le fluor 18.
Le fluor 189F est utilisé comme traceur en imagerie médicale.Il se désintègre selon une radioactivité de type ß+ ; sa demi-vie est de 110 minutes.
La masse du noyau de fluor 18 est m1 = 17,9960 u. 1,00 u = 1,66 10-27 kg.
1. Ecrire l'équation de
désintégration du fluor 18. Quelle est la composition du noyau fils
obtenu et le nom de la particule émise ?
189F
---> 01e
+AZX.
Conservation de la charge : 9 = 1 +Z d'où Z = 8, élément oxygène.
Conservation du nombre de nucléons : 18 = 0 +A d'où A = 18.
189F
---> 188O
+01e.
188O : 8 ptotons et 18-8 = 10 neutrons.
Emission d'un positon 01e.
2. Dans l'extrait de la
classification périodique des éléments, il n'est pas mentionné le fluor
18 mais le fluor 19. Expliquer cette différence.
Le fluor 18 et le fluor 19 sont isotopes. Dans la classification périodique, les isotopes les plus stables y figurent.
3. Définir temps de demi-vie.
C'est la durée au bout de laquelle l'activité initiale est divisée par deux.
4. Déterminer la valeur de la constante radioactive du fluor 18.
l = ln2 / t½ = ln2 / 110 =6,30 10-3 min-1 ou 1,05 10-4 s-1.
5.
On souhaite administrer au patient, une dose de fluor 18 dont
l'activité est A = 180 MBq. Déterminer le nombre de noyaux de fluor 18
que cela représente. Calculer, en kg, la masse de fluor correspondante.
Conclure.
N0 = A / l = 180 106 / (1,05 10-4) =1,71 1012.
Masse correspondante : m =N m1 = 1,71 1012 *17,9960*1,67 10-27 =5,15 10-14 kg, valeur très faible.
6. A t=0, on administre au patient la dose décrite à la question précédente. Calculer l'activité du fluor 18 au bout d'une heure.
A = A0 exp(-lt) = 180 exp(-6,30 10-3*60)=123 MBq.
7.
Déterminer la durée nécessaire pour que l'activité du fluor 18 ne soit plus que de 1,0% de l'activité à t = 0.A / A0 = 0,010 = exp(-6,30 10-3t ) ; ln 0,010 = -6,30 10-3t ; t ~7,3 102 minutes.
8. On souhaite calculer les
valeurs de l'activité au cours du temps par la méthode d'Euler. On
choisit un pas d'itération de 100 s. La valeur est-elle compatible avec
ce système ?
Oui, 100 s = 1 min 40 s, soit à peu près 1,5 % du temps de demi-vie.
En prenant toujours A = 180 MBq à t=0, déterminer par la méthode d'Euler, l'activité à t = 100 s et à t = 200 s.
A t=0, A0 = 180 MBq.
DA = -lADt = -1,05 10-4 *180 *100 =-1,89 Bq.
A (0+Dt) =A0 + DA = 180-1,89 ~ 178 Bq.
DA = -lADt = -1,05 10-4 *178 *100 = -1,87 Bq.
A (0+2Dt) =A + DA = 178-1,87 ~ 176 Bq.
9. La masse du noyau de fluor 18 est m1 = 17,9960 u. Celle du noyau fils est m2 = 17,9948 u. Celle de la particule émise est m3 = 5,48 10-4 u.
Calculer l'énergie dégagée lors de la désintégration d'un noyau de fluor 18.
Variation de masse |Dm| =m1-m2-m3 = 17,9960-17,9948-5,48 10-4=6,52 10-4 u ou 6,52 10-4 *1,67 10-27 =1,09 10-30 kg.
Energie dégagée E = |Dm| c2=9,8 10-14 J.
En déduire l'énergie que reçoit le patient lors de la première seconde de traitement
Nombre de noyaux se désintégrant en une seconde : 180 106.
Energie correspondante : 180 106 *9,8 10-14 =1,76 10-5 J.
|
|