Déviation d'un
faisceau d'électrons.
Concours orthoptie Rennes 2015.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Exercice 1.
Dans
un oscilloscope analogique, un faisceau d'électrons émis en un point C,
avec une vitesse initiale quasi nulle, est accéléré par une tension U0 entre les points C et E situés sur un axe Ox.
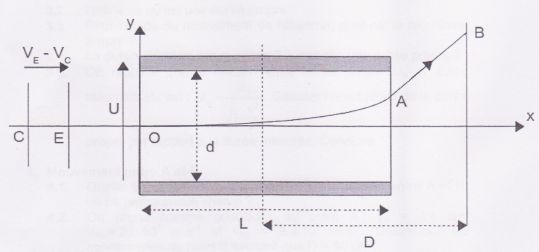
Puis il pénètre en O, avec une vitesse v0, dans un champ
électrique E supposé uniforme régnant entre deux plaques parallèles
métalliques symétriques par rapport au plan xOy, de longueur L = 20 cm
et séparées par une distance d, avec E = 5,0 103 V m-1.
Le champ est créé par une tension U appliquée entre ces plaques. Le
faisceau sort en A de la zone où règne le champ, puis il atteint
finalement l'écran de l'oscilloscope en un point B ( spot lumineux ).
On néglige le poids de l'électron.
1. Mouvement entre C et E.
1.1. Quel doit être le signe de la tension accélératrice VE-VC ? Justifier.
Pour être accéléré, l'électron de charge -e doit être soumis à une force dont le travail est moteur.
Travail de la force électrique entre C et E : W = -e(VC-VE).
VC-VE <0, soit VE-VC >0.
1.2. Donner l'expression du travail de la force électrique qui s'exerce sur l'électron entre C et E.
W = e ( (VE-VC).
1.3. Exprimer la norme v0 de la vitesse en O d'un électron de masse m, de charge -e en fonction de U0 = |VE-VC|.
Théorème de l'énergie cinétique entre C et E :
½mv02-0 = eU0 ; v0 =( 2eU0 / m)½.
1.4. Calculer v0 et montrer qu'elle n'est pas très éloignée de 2 107 m/s, valeur que l'on retiendra par la suite. U0 = 1000 V.
v0 =(2*1,6 10-19 *1000 / (9,1 10-31))½ = 1,87 107 m/s ~2 107 m/s.
|
| .
. |
|
|
2. Mouvement entre O et A.
2.1. Dans le repère xOy, donner les coordonnées du vecteur accélération d'un électron entre O et A.
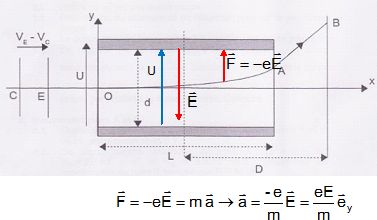
2.2. En déduire les équations horaires de l'électron entre O et A.
La vitesse est une primitive de l'accélération : vx = v0 , vy =eE/m t.
La position est une primitive de la vitesse : x = v0t ; y = ½eE/mt2.
2.3. Calculer la durée du parcours entre O et A.
L = v0t ; t = L / v0 = 0,20 / (2 107) =1 10-8 s.
2.4. Montrer que la valeur de la vitesse varie peu entre O et A.
vy = eE/mt = 1,6 10-19 *5,0 103 /(9,1 10-31) *1 10-8 =8,8 106 m/s.
v = (vx2+vy2)½=[4 1014 + (8,8 106)2]½=2,2 107 m/s.
L'écart est de l'ordre de 10 %.
2.5. Déterminer l'équation de la trajectoire d'un électron entre O et A. Quelle est la nature de cette trajectoire ?
t = x /v0, repport dans y :
y = ½eE x2 / (mv02). Branche de parabole.
2.6. En déduire l'ordonnée yA du point A.
yA = ½eE L2 / (mv02) avec E = U / d.
yA = ½e L2 / (mdv02) U = k U avec k une constante.
yA est proportionnelle à U.
|
|
|
|
3. Relativité du temps entre O et A.
On admet que la vitesse de l'électron entre O et A est 2 107 m/s et qu'elle ne varie pratiquement pas.
3.1. A quelle valeur faut-il comparer v0 pour montrer le caractère relativiste de l'électron ?
On compare v0 et c = 3 108 m/s, vitesse de la lumière dans le vide.
3.2. Définir ce qu'est une durée propre.
La durée propre Dtp est la durée séparant deux événements mesurée par une horloge fixe dans le référentiel de la particule.
3.3. Pour l'étude du mouvement de l'électron, quel est le référentiel propre ?
Le référentiel lié à l'électron est le référentiel propre.
3.4. La durée calculée à la question 2.3 est-elle une durée propre ?.
Non, cette durée Dtm est mesurée dans un référentiel galiléen, en mouvement par rapport au référentiel lié à l'électron.
3.5. Calculer l'écart relatif de la durée propre par rapport à la durée mesurée. Conclure.
Dtm = Dtp [1-v2/c2]-½.
(v / c )2= [2 107 /(3 108)]~4,4 10-3, petit devant 1.
Dtm ~ Dtp [1+v2/(2c2)]
(Dtm - Dtp ) / Dtp ~v2/(2c2)~2,2 10-3.
L'électron n'est pas relativiste.
4. Mouvement entre A et B.
4.1. Quelle est la nature du mouvement d'un électron entre A et B où ne règne aucun champ ?
L'électron n'est soumis à aucune force. D'après le principe d'inertie le mouvement de l'électron est rectiligne uniforme à la vitesse v0.
4.2. Au point A : yA = 4,4 cm ; vAx = 2 107 m/s ; vAy = 8,8 106 m/s.
Déterminer les coordonnées du point B si D = 30 cm.
Coefficient directeur de la tangente à la parabole en A : vAy / vAx =0,88 / 2 = 0,44.
Equation de cette tangente : y = 0,44 x+ b avec b = yA-0,44 xA = 0,044-0,44*0,2 = -0,044.
y = 0,44 x -0,044. La tangente coupe l'axe des x à l'abscise 0,10 m.
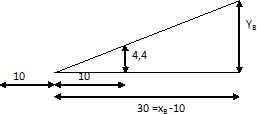
xB = 40 cm ;
yB = 0,44*0,4 -0,044 = 0,132 m~ 13 cm.
|
|
|
|