Lentilles et
miroirs, radioactivité. Concours orthoptie Amiens 2009.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
I.
Quelle est la célérité d'une onde lumineuse dans un milieu d'indice
absolu n = 1,5 ?
v = c / n = 3,0 108 / 1,5 = 2,0
108 m/s.
II. Un rayon
lumineux traverse une plaque de verre ( n = 1,5) et pénètre dans l'eau
( n = 1,33 ). A l'interface verre / eau.
1. Quelle est la
valeur de l'angle de réfraction si le rayon incident fait un angle de
60° par rapport à la surface de l'eau ?
Tous les angles sont repérrés par rapport à la perpendiculaire à la
surface de l'eau.
nverre sin i = neau sin r avec i = 30°.
sin r = 1,5 sin 30 / 1,33 = 0,564 ; r = 34,3 ~34°.
2. Quelles sont les
valeurs maximales que peuvent prendre l'angle d'incidence et l'angle de
réfraction ?
Angle de réfraction maximum : 90°.
Angle d'incidence correspondant : 1,5 sin ilim = 1,33 * sin
90 = 1,33.
sin ilim =1,33 / 1,5 = 0,887 ; ilim = 62°.
3. Que se passe
t-il si le rayon lumineux arrive sur l'eau avec un angle d'incidence de
valeur supérieure à la valeur maximale trouvée précédemment ?
Il y a réflexion totale : le
rayon ne pénètre pas dans l'eau, il est réfléchi entièrement dans le
verre.
III. Un objet AB
de20 cm de haut est placé, perpendiculairement à l'axe optique, à 1 m
d'un miroir plan.
1. Faire une
construction géométrique de l'image A'B' et expliquer les tracés
effectués.
L'image est symétrique de l'objet par rapport au miroir.
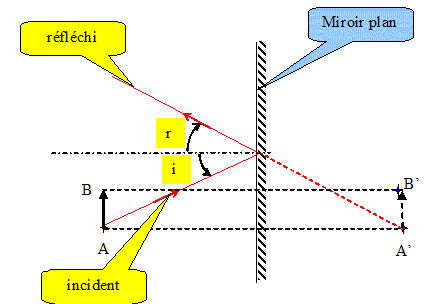
2. Où se trouve l'image et quelles
sont ses caractéristiques ( nature, sens, grandeur ) Justifier.
L'image est symétrique de l'objet par
rapport au miroir, donc image virtuelle, de même sens et de même
hauteur que l'objet.
|
| .
. |
|
|
IV.
Un objet réel de 15 cm de haut est placé perpendiculairement à l'axe
optique, à 50 cm d'un miroir sphérique concave de 20 cm de rayon.
1. Où se trouvent
les foyers objet et image ?
Les deux foyers principaux sont confondus et se trouvent au milieu du
segment SC ( avec S sommet du miroir et C son centre).
2. Faire la
construction géométrique de l'image et expliquer les tracés effectués.
Un rayon passant par le foyer F est réfléchi parallèlement à l'axe
optique.
Un rayon passant par le centre de la sphère C est réfléchi sur lui même.
Un rayon passant par le sommet S du miroir est réfléchi avec le même
angle par rapport à l'axe optique.
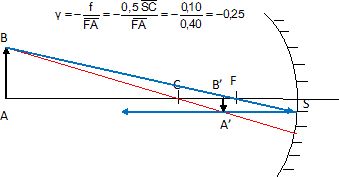
3. En déduire les
caractéristiques de l'image.
L'image est réelle, plus petite et
inversée.
|
|
|
|
V. Soit une lentille L1,
plan concave en verre d'indice n = 1,5 dont le deuxième rayon de
courbure est égal à R2= 60 cm.
1. Quelle est la vergence de la lentille et quelle est sa nature ?
La lentille peut être considérée comme mince.
V1 = (n-nair) [1/ R1-1/R2] =(1,5-1) * [0-1/ 0,60] = -0,83 d ; elle est divergente.
2. Calculer la distance focale f1 de la lentille.
f1 = 1/V1 = -1/0,83 = -1,2 m.
3. Un objet réel AB de 10 cm de haut est placé perpendiculairement à
l'axe optique, à 70 cm de la lentille L1.
a. Déterminer la position de son image à travers cette lentille. Quelle
est la nature de l'image ?
b. Calculer le grandissement. En déduire le sens et la grandeur de
l'image.
c. Faire la construction géométrique de l'image.
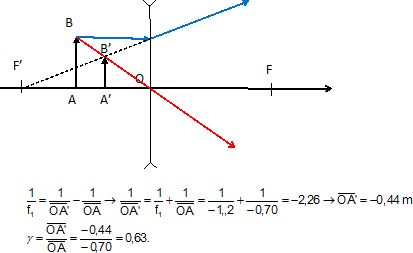
L'image est virtuelle, droite, de hauteur 6,3 cm.
4. On forme une lentille L3 en accolant à la lentille L1, une lentille
L2 biconvexe de rayon 60 cm et 30 cm et de même indice que L1.
a. Faire un dessin représentant l'association des deux lentilles.
Le schéma n'est pas à l'échelle, l'épaisseur reste faible devant les rayons de courbures.
b. Quelles sont les vergence et la nature de la lentille L2 ?
La lentille peut être considérée comme mince.
V2 = (n-nair) [1/ R1-1/R2] =(1,5-1) * [1/0,30-1/ 0,60] = +0,83 d ; elle est convergente.
c. Quelles sont les vergence et la nature de la lentille L3 ?
Pour des lentilles minces accolées, les vergences s'ajoutent : -0,83 +0,83 = 0.
d. Où se situe l'image de l'objet AB à travers la lentille L3 et quelle
est sa nature ? Quel est le grandissement obtenu ? En déduire le sens
et la grandeur de l'image.
Les lentilles accolées sont équivalentes à un simple lame de verre. La lentille L3 n'a pas de foyer et le grandissement vaut 1.
|
VI. 1. Soit un élément X dont le noyau est représenté par AZX. Que représnetent les lettres A et Z ?
A : nombre de nucléons ; Z : numéro atomique, nombre de protons.
2. Donner la composition du noyau 2311Na.
11 protons et 23-11 = 12 neutrons.
3. Que représentent les deux noyaux 126C et 136C ? Pourquoi ?
Ce sont des isotopes, ils ne diffèrent que par leur nombre de neutrons.
VII. 1. Dans le diagramme N = f(Z), où se situent les noyaux émettant des particules ß+ et ceux qui émettent des particules ß- ?
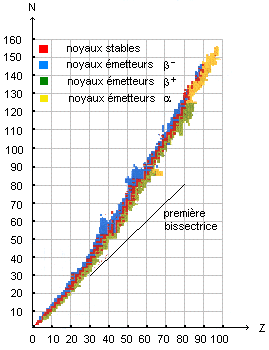
Donner une définition de ces deux types de noyaux et écrire la réaction qui se produit dans chacun d'entre eux.
Ecrire l'équation générale de désintégration.
Radioactivité de type ß- : un neutron du noyau se transforme en proton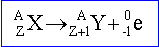 en émettant un électron. en émettant un électron.
Radioactivité de type ß+ : un proton du noyau se transforme en neutron en émettant un positon. en émettant un positon.
VIII. Définir la période T ou demi-vie d'un élément radioactif.
T : durée au bout de laquelle l'activité initiale est divisée par deux.
Définir la constante radioactive l et donner son expression en fonction de la période.
l = ln2 / T.
l = dP
/ dt, probabilité qu'à un noyau de subir une transformation nucléaire
spontanée, à partir d'un état d'énergie défini, dans l'intervalle de
temps dt.
IX. Quelle est l'activité d'un gramme d'iode 131 ?.
T = 8 jours ; M(131I )= 131 g/mol ; NA = 6,02 1023 mol-1.
Nombre de noyaux d'iode / = 1 / 131 *6,02 1023 =4,6 1021.
l = ln2 /(8*24*3600)= 1,0 10-6 s-1.
A = l N = 4,6 1021 *1,0 10-6 = 4,6 1015 Bq.
X. Aujourd'hui, un échantillon d'iode 131 a une activité de 16 106 Bq.
1. Exprimer cette activité en curie.
1 Ci = 3,7 1010 Bq. 16 106 / (3,7 1010) = 4,3 10-4 Ci.
2. Quelle étaient les activités de cet échantillon il y a 10 jours, il y a 8 jours ?
Activité il y a 8 jours : 32 106 Bq.
Activité il y a 12 jours :
l = ln2 / 8 =8,66 10-2 j-1.
A = A0 exp(-lt) ; A0 = A exp(-lt) = 16 106 exp(8,66 10-2 *12)=4,5 107 Bq.
3. Quelles seront les activités de cet échantillon dans 8 jours, dans 12 jours et dans 16 jours ?
Dans 8 jours : A = 8 106 Bq ; dans 16 jours A = 4 106 Bq.
Dans 12 jours A =16 106 exp(- 8,66 10-2*12)=5,7 106 Bq.
|
|