Ondes
ultrasonores, relativité restreinte. Concours orthoptie Nantes
2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
A-
Ultrasons dans l'air.
Célérité du son dans l'air à 25°C : vair = 340 m/s ;
fréquence de l'émetteur f = 40 kHz.
1. Déterminer la
longueur d'onde de l'onde ultrasonore générée.
l = vair
/ f = 340 / 40000 =0,0085 m = 8,5 mm.
2. La source est
disposée à une distance d d'un récepteur lui faisant face.
Définir le retard avec lequel les vibrations sont transmises au
récepteur. Le calculer pour d = 50 cm.
Dt = d
/vair = 0,50 / 340 = 1,47 10-3 s = 1,47 ms.
3. Avec quel
instrument de mesure ce retard peut-il être correctement évalué ?
Justifier la réponse.
On utilise un oscilloscope : voie 1 relié à l'émetteur ( en mode salves
) et voie 2 relié au récepteur. Le retard est déterminé en observant le
décalage des deux courbes et en utilisant la base de temps ( 1 ms / div
).
4. Face à la source ultrasonore, réglée
comme précédemment, on place à 10 cm une plaque de métal trouée d'une
fente rectangulaire verticale de largeur réglable, disposée selon le
schéma ci-dessous ( vue de dessus). On déplace le récepteur en le
maintenant à une distance constante de 40 cm de la fente.
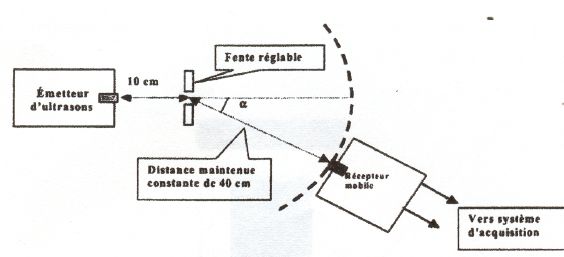
Un
système d'acquisition permet de mesurer la tension aux bornes du
récepteur. On repère la valeur de l'angle a correpondant aux maximas
et aux minimas d'amplitude successive de la tension sinusoïdale
mesurée. On donne les résultats obtenus pour une largeur de fente égale
à 40 mm
Angle
a
(°)
|
0
|
12
|
18
|
25
|
Amplitude
de la tension
|
Maximum
|
Minimum
|
Maximum
|
Minimum
|
a. Quel phénomène physique est mis
en évidence par cette expérience ? La largeur de la fente a t-elle une
influence sur ce phénomène ? Expliquer.
Lorsque la largeur de la fente est du même ordre de grandeur que la
longueur d'onde, on observe un phénomène de diffraction. Ce dernier est
dautant plus marqué que la largeur de la fente est proche de la
longueur d'onde. Ce phénomène n'apparaît pas si la largeur de la fente
est très supérieure à la longueur d'onde.
b. Tous les autres
paramètres de l'expérience restant inchangés, la largeur de la fente
est réduite à 20 mm. Dans quel sens varie l'angle d'observation du
premier minimum ? Justifier.
Si l'ouverture
est plus petite on s'attend donc à ce que tous les angles mesurés précédemment soient plus grands, le faisceau
diffracté s'élargissant.
|
| .
. |
|
|
B. Principe du
sonar.
Le sonar est un dispositif
émetteur-récepteur d'ondes
ultrasonores qui, remorqué par un navire, permet d'obtenir des
enregistrements donnant une image à deux dimensions des fonds marins.
Les dispositions de l'émetteur et du récepteur sont représentées
schématiquement ci-dessous :
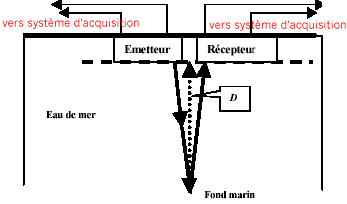
Les "rayons ultrasonores" qui matérialisent la direction
et le sens de propagation de l'onde ultrasonore sont très peu inclinés
par rapport à la verticale. On considérera donc que le trajet accompli
par l'onde (de l'émetteur vers le fond marin puis, après réflexion, du
fond marin vers le récepteur) se fait quasiment selon la verticale.
On
utilise ici une tension sinusoïdale de fréquence f ' =
20 kHz pour alimenter l'émetteur, la longueur d'onde dans le milieu
marin étant alors l=
7,5 cm.
1. Calculer la
célérité veau des ondes émises.
veau = l
f ' =0,075 * 20 000 = 1,5 103 m/s.
L'onde n'est pas générée par l'émetteur en continu
mais par
trains d'ondes d'une durée de 0,010 s émis toutes les secondes.
Un système
d'acquisition permet de visualiser la tension Ue
aux bornes de l'émetteur en fonction du temps. On obtient la
représentation suivante montrant deux trains d'ondes successifs S0
et S1
(fig. B1). Une visualisation de S0 est également
proposée avec une
échelle de temps plus petite afin de voir les détails du signal (fig.
B2) :
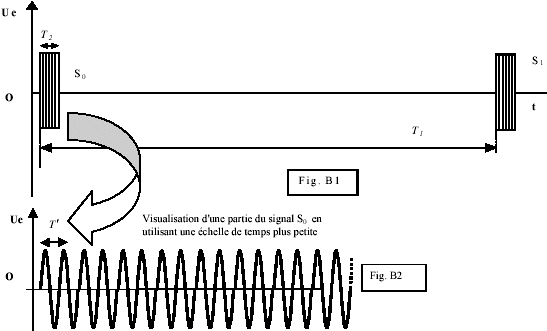 Utiliser les données du
texte précédent pour déterminer
les durées T ', T1 et T2
indiquées sur les
schémas. Justifier, le cas échéant, par des calculs.
Utiliser les données du
texte précédent pour déterminer
les durées T ', T1 et T2
indiquées sur les
schémas. Justifier, le cas échéant, par des calculs.
T ' = 1 / f ' = 1 / 20000
= 5 10-5 s = 50 µs.
T1 = 1 s ; T2 = 0,010 s.
|
|
|
|
On visualise maintenant une
acquisition qui superpose la
tension Ue aux bornes de l'émetteur (signaux S0, S1..
) et la tension Us aux bornes du récepteur ( signaux e0,
e1
. ). Les traces e0, e1, e2, e3
matérialisent les différents échos détectés par le récepteur.
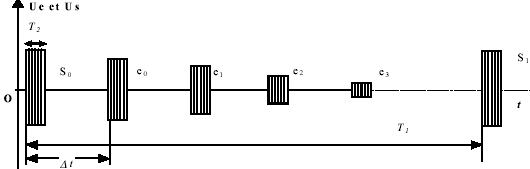
On appelle Dt le décalage de
temps du premier écho e0 avec le déclenchement du premier
signal électrique à t = 0 s. La valeur de D t
est suffisamment faible pour que l'on considère l'ensemble
émetteur-récepteur comme fixe par rapport au fond pendant cette durée.
Calculer la profondeur D du fond marin en un lieu où D t = 0,10s.
Dt =
2D/ veau car le
trajet accompli par l'onde correspond à un aller-retour entre
l'émetteur et le récepteur.
Soit D= Dt veau/2
=0,1× 1500/2 = 75 m.
- Proposer une explication pour l'existence d'échos multiples à
intervalles de temps réguliers.
- Pourquoi leur amplitude décroît-elle ?
L'onde qui arrive
sur le récepteur peut se réfléchir sur lui et être reçue à nouveau
après un aller-retour de plus et ainsi de suite. Les
intervalles de temps entre les échos sont réguliers car la distance
parcourue,
lors de chaque
aller-retour est la même. Cela suppose que le bateau se
déplace très lentement ou bien est à l'arrêt.
L'amplitude
décroît car l'onde s'amortit au fur et à mesure qu'elle se propage car
l'énergie de la source se répartit sur une sphère de plus en plus grande.
Relativité restreinte.
1. On considère un sprinter évoluant à une vitesse v = 10 m/s dans un référentiel terrestre.
a. Calculer le facteur de Lorentz g correspondant à cette vitesse.
g = [1-v2/c2]-½ = [1-102/(3 108)2]-½ ~1,00.
b. Commenter ce résultat et ces conséquences.
La relativité restreinte concerne les très gandes vitesses et non pas les vitesses à l'échelle humaine.
c. Donner le principal postulat d'Einstein sur lequel est basé la relativité restreinte.
Les lois de la physiques sont les mêmes pour tous les observateurs se trouvant dans des référentiels inertiels.
La valeur de la vitesse de la lumière dans le vide a même valeur dans
toutes les directions et dans tous les référentiels inertiels.
2. Proxima Centauri est l'étoile la plus proche du soleil : elle se
situe à une distance d = 4,22 années lumière de distance. Un
astronef parti de la terre et voyageant à une vitesse v voit ses
passagers vieillir de DTastronef = 3,0 ans durant un aller simple vers Proxima Centauri.
a. Définir une année lumière.
C'est la distance parcourue par la lumière dans le vide à la célérité c pendant une année.
b. Montrer que D = 4,00 1016 m.
D = 4,22 *3,00 108*3600*24*365 =4,00 1016 m.
c. La durée DT de ce voyage vu depuis la terre est-elle un temps propre ou un temps mesuré ?
DT est un temps mesuré.
d. Déterminer l'expression de cette durée DT en fonction de D et v.
DT = D / v.
e. Quelle relation existe-t-il entre DT et DTastronef.
DT = g DTastronef.
f. Montrer que la vitesse v de l'astronef est donnée par : v = D c / [DT2astronef c2 +D2]½.
DT = D / v = 1 /[1-v2 /c2]½ DTastronef.
Elever au carré : D2 / v2 = 1 /[1-v2 /c2] DT2astronef.
D2 / v2 [1-v2 /c2] = DT2astronef.
D2 / v2 - D2 / c2 =DT2astronef.
D2 / v2 = DT2astronef + D2 / c2 = [D2 + c2 DT2astronef ] / c2].
v2 = D2 c2 / [D2 + c2 DT2astronef ]
v= D c / [D2 + c2 DT2astronef ] ½.
g. Calculer v à laquelle se déplace l'astronef par rapport à la terre.
v = 4,00 1016 *3,00 108 / [16 1032 +9 1016 *(3,0 *365*24*3600)2]½ = 2,45 108 m /s.
h. Calculer le facteur de Lorentz correspondant à la vitesse de l'astronef et conclure.
v2 / c2 =(2,45 / 3)2 =0,665 ; 1-0,665 =0,335 ; g = 1 / 0,335½ =1,73 ~1,7.
Les horloges en mouvement sont plus lentes quand elles sont observées par un observateur au repos.
Vu de la terre, la durée du voyage aller est environ 3,0*1,7 ~5 ans.
|
|



