Pendule simple,
électrons relativiste.
Concours kiné Berck 2016.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
1.Pendule
simple.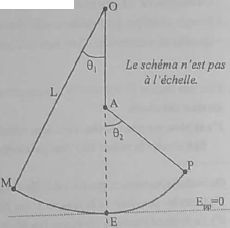
On écarte le pendule, fil tendu, de la verticale d'un angle q1.Le solide
ponctuel se trouve en M et on le lâche sans vitesse initiale. Lorsque
le pendule passe par la verticale du point O, il rencontre un clou fixé
en A. La partie OA reste bloquée. Le solide remonte jusqu'au point P.
On néglige les frottements ; la référence de l'énergie potentielle est
le point E. On note AE = L'.
Masse du solide ponctuel m = 250 g ; L = 52,3 cm ; q1 = 25,0° ; q2 = 57,4 °.
1. Calculer
l'énergie mécanique du solide ponctuel.
L'énergie mécanique reste constante, en absence de frottement.
L'énergie mécanique initiale est sous forme potentielle et vaut :
mgL(1-cos q1) =0,250 *0,523(1-cos25)=0,120 J ~120 mJ.
2. En déduire la vitesse vE
du solide au passage en E.
En E, l'énergie mécanique du solide est sous forme cinétique.
½mvE2 = 0,01255 ; vE2
=2*0,120 / 0,25 =0,96 ; vE =
0,98 m /s.
3.
Calculer OA en cm.
L'énergie mécanique en P est sous forme potentielle et vaut :
mgAP(1-cos q2) =0,120 ; AP = 0,120 / [mg(1-cos q2) ].
AP = 0,120 / [0,25*9,8(1-cos57,4)]=0,106 m.
OA = L-AP=0,523-0,106 =0,417 m = 41,7 cm.
4. Déterminer la valeur de la
tension T ( en N ) exercée par le fil sur le solide en P.
La vitesse du solide en P est nulle.
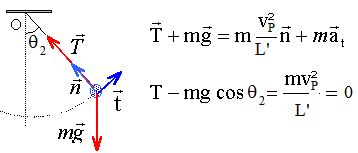
T = 0,25 *9,8 *cos 57,4 = 1,32 N.
|
|
|
On écarte le pendule, fil
tendu, d'un nouvel angle q1 et on le lâche sans vitesse initiale. La
position du clou reste inchangée. On mesure q2 = 47,8°.
5. Calculer q1 ( en ° ).
L'énergie
mécanique reste constante, en absence de frottement.
L'énergie mécanique initiale est sous forme potentielle et vaut :
Em =mgL(1-cos q1).
L'énergie mécanique en P est sous forme potentielle et vaut :
Em
=mgL'(1-cos q2).
L' = L -OA = 0,523-0,417 = 0,106 m.
mgL(1-cos q1) = mgL'(1-cos q2).
L(1-cos q1) =L'(1-cos
q2).
1-cos q1) =L'
/ L(1-cos q2).
cos q1 =1-L' / L(1-cos q2) = 1-0,106 / 0,523 (1-cos47,8)=0,9334
; q1= 21,0.
|
|
|
|
Electron dans un champ électrique.

Les électrons sont émis de la cathode C avec une vitesse négligeable.
Ils sont accélérés horizontalement entre A et C, sous l'action d'une
tension électrique U. Le poids des électrons est négligeable. On admet
que les électrons sont animés d'un mouvement rectiligne uniforme entre
les détecteurs D1 et D2. On note v la vitesse
correspondante.
On donne L = 8,40 m ; U peut varier de 0 à 15,0 MV. Masse d'un électron
m = 9,11 10-31 kg.
Pour U = 1,00 105
V, on mesue une durée Dt
= 51,1 ns pour que les électrons parcourent la distance L.
1.a. Montrer que
les électrons sont relativistes.
v = L / Dt = 8,40
/ (51,1 10-9) =1,64 108 m/s.
0,14 c = 0,14 *3,00 108 =4,2 107 m/s.
v étant supérieure à 0,14 c, les électrons sont relativistes.
1.b.. Calculer
leur énergie cinétique ( en k eV ).
Ec = eU en joule ; Ec / e = U =1,00 105
eV = 100 keV.
On souhaite maintenant produire des électrons relativistes dont la
vitesse mesurée entre les détecteurs est v = 0,985 c.
2. Calculer la valeur de la tension
U.
Ec = (g-1) mc2 = eU.
g=[1-v2/c2]-½
=(1-0,9852)-½ = 5,795.
U = (g-1) mc2
/ e = 4,795 *9,11 10-31*9 1016 / (1,6 10-19)=2,46
106 V = 2,46 MV.
3. En déduire
l'énergie cinétique de ces électrons ( en MeV).
Ec = eU =2,46 MeV.
4. Calculer la
longueur d'onde l
( en pm) associée à ces électrons.
p = gm v = h / l ; l
= h / ( gmv) ;
l
=6,63 10-34 / (5,795 *9,11 10-31 *0,985 *3 108)=
4,25 10-13 m =0,425 pm.
On accélère ces électrons sous une tension U =
15,0 MV
5. Calculer la
durée Dt ( en ns)
du parcours L.
Ec = (g-1) mc2 = eU=
1,6 10-19 *15,0 106 =2,4 10-12 J
g = 1+2,4
10-12 / (mc2)=1+2,4 10-12 /
(9,11 10-31*9 1016)=30,27.
g=[1-v2/c2]-½
; 1/g2=1-v2/c2
; v2/c2 =1-
1/g2=1-1 / 30,272
= 0,99891 ; v = 0,99945 c ~3 108 m /s.
Dt
= 8,4 / (3 108) ~2,8 10-8 s = 28 ns.
|
|