QCM Physique. Concours kiné EFOM 2016.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.



. .



.
.


Exercice 12.
Un guitariste utilise un diapason pour accorder son instrument. Il ajuste ainsi la fréquence du son émis par la guitare sur celle du son émis par le diapason. Un dispositif a permis d'obtenir les enregistrements ci-après, correspondant respectivement au diapason et à la guitare jouant seuls.

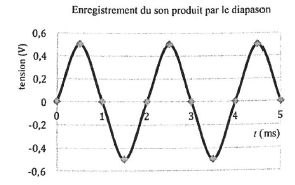
a. La fréquence du son émis par le diapason vaut 500 Hz. Vrai.
T = 2 ms ; f = 1/0,002 = 500 Hz.
 b. La longueur d'onde du son émis par le diapason vaut 6,8 cm. Faux.
l = c / f = 340 / 500 = 0,68 m = 68 cm.
.
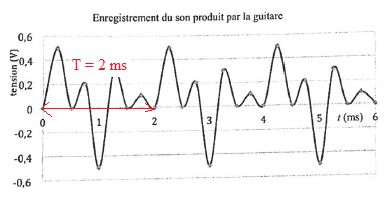c. La guitare et le diapason ne sont pas accordés car leurs sons n'ont pas la même hauteur. Faux.
La fréquence du fondamental du son émis par la guitare est égale à celle du diapason..
d. Il est possible d'observer un phénomène d'interférences entre ces deux sons. Faux.

Exercice 13.
Un son pur est un son qui n'a pas d'harmonique. Un diapason émet un son pur de fréquence 680 Hz. A une certaine distance du diapason, un auditeur perçoit un son de niveau d'intensité sonore L.
a. Une personne située à 34 m du diapason perçoit un son produit avec un retard de 100 ms.Vrai.
t = d / v = 34 / 340 = 0,1 s = 100 ms. Vrai.
b. La longueur d'onde du son produit dans l'air vaut 50 cm.
l = v /f =340 / 680 = 0,5 m = 50 cm. Vrai.
c. Pour une intensité sonore perçue de 1,0 10-10 W m-2, le niveau d'intensité sonore est de 2 dB. Faux.
L = 10 log ( 1,0 10-10 / 10-12) = 20 dB.
d. Si on ajoute 3 diapasons identiques au précédent, jouant chacun avec la même intensité sonore en même temps, l'intensité sonore perçue par le même auditeur est multipliée par quatre. Vrai.

 Exercice 14.
Un pendule simple est constitué d'un fil inextensible de longueur l, de masse négligeable devant celle m d'une boule supposée ponctuelle attachée à son extrémité. Après avoir écarté le pendule d'un angle a par rapport à la verticale, on lâche le pendule sans vitesse initiale. Lorsque le pendule passe par la verticale, il rencontre un clou situé à mi-longueur du fil, et s'écarte alors au maximum d'un angle ß par rapport à la verticale. On néglige les forces de frottements.

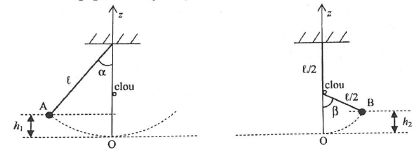
m = 50 g ; h1 = 20 cm ; g = 10 m s-2.
 a. Le travail du poids est positif lorsque le point d'application de cette force passe du point A au point O. Vrai.
b. La boule passe en O avec une vitesse v = 4,0 m/s. Faux.
 L'énergie mécanique reste constante, en absence de frottement.
L'énergie mécanique initiale est sous forme potentielle et vaut : mgh1 = mgl(1-cos a)
 L'énergie mécanique en O est sous forme cinétique et vaut ½mv2.
mgh1 =½mv2 ; v = (2gh1)½ = (20*0,20)½ =2,0 m/s.
c. Lors du passage en O, l'énergie cinétique de la boule vaut 100 mJ. Vrai.
½mv2 = 0,5 *0,050 *22 =0,10 J = 100 mJ.
d. Si a = 60° alors la boule remonte en B tel que ß = 90°. Vrai.
L'énergie mécanique en B est sous forme potentielle :  mg l/2(1-cos ß) = mgl(1-cos a)
1-cos ß = 2(1-cos a) ; cos ß =2(1-cos a)-1 = 2(1-cos60)-1 =  0 ; ß = 90°.

 Exercice 15.
Dans le référentiel terrestre supposé galiléen, on étudie le mouvement d'un objet de masse m = 1,0 kg lancé verticalement vers le haut avec une vitesse initiale v0 = 2,0 m/s. On suppose que l'objet n'est soumis qu'à son poids.
a. Le vecteur accélération initial est dirigé vers le haut. Faux.
Le vecteur accélération est vertical, vers le bas, valeur g = 10 m s-2.
b. L'accélération a une valeur d'autant plus élevée que l'objet a une masse importante. Faux.
c. L'énergie mécanique de l'objet reste constante au cours du mouvement. Vrai.
d. L'objet va s'élever d'une hauteur de 40 cm avant de retomber. Faux.
Conservation de l'énergie mécanique ½mv02 = mgh ; h = v02 /(2g) =4 / 20 =0,20 m.




Exercice 16.
Un ressort à spires non jointives, de longueur à vide l0 = 20 cm et de constante de raideur k = 100 N m-1 est attaché à un solide (S) de masse m1 = 750 g alors que son autre extrémité est fixe. La masse du ressort est négligeable devant m1. Le ressort est enfilé sur une tige horizontale et un dispositif convenable assure le guidage de l'ensemble. Le ressort n'étant ni étiré, ni comprimé et le solide étant au repos, un solide S2 de masse m2 = 250 g heurte le solide S1 avec une vitesse v2 = 1,0 m/s suivant l'axe du ressort. Après le choc, les deux solides restent accrochés.
On considère que le ressort n'exerce aucune force sur le solide S1 pendant le choc et que toutes les forces dissipatives d'énergie sont négligées devant les autres actions mécaniques.

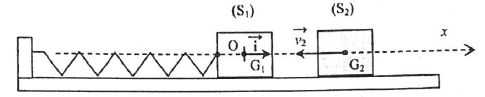
a. La quantité de mouvement du solide S2 vaut 250 SI. Faux.
mv2 = 0,250 *1,0 = 0,25 kg m s-1.
b. Immédiatement après le choc, l'ensemble des deux solides accrochés possède une vitesse de 0,25 m /s.  Vrai.
Conservation de la quantité de mouvement : 0,25 = (m1+m2)v ; v = 0,25 / 1 = 0,25 m/s.
c. Dans les premiers instants qui suivent le choc, pendant lesquels le ressort se comprime, l'énergie mécanique du système {solide S1 +solide S2 } augmente. Faux.
d. La longueur minimale du ressort au cours des oscillations est de 15 cm. Vrai.
Conservation de l'énergie mécanique : ½m2 v22 = ½k(lmini-l0)2 .
(lmini-l0)2 =m2 v22 / k ; l0-lmini = (m2/k)½v2 = (0,25 /100)½ *1,0 =0,05 m = 5,0 cm.
lmini =20 -5 = 15 cm.

Exercice 17.
Deux patineurs, notés A et B, de même masse sont côte à côte et immobiles sur une patinoire horizontale. On suppose que la patinoire est parfaite : les frottements sont nuls. A un instant donné, le patineur A exerce une force horizontale sur le patineur B afin de l'éloigner. Après leur séparation, on mesure leurs vitesse respectives vA et vB dans le référentiel terrestre.
a. La poussée ne modifie pas l'énergie mécanique de chacun des deux patineurs.. Faux.
L'énergie mécanique des deux patineurs augmente du travail de cette poussée.
b. Lors de cette poussée, le patineur B exerce une force sur le patineur A. Faux.
Le patineur B s'éloigne très rapidement de A.
c. Après la poussée, les vitesses vA et vB ont la même valeur. Vrai.
  Le vecteur quantité de mouvement des deux patineurs se conserve et les masses de A et B sont égales.
d. Si le patineur A avait une masse supérieure à celle de B, la vitesse vA serait plus faible que la vitesse vB. Vrai.









Exercice 18.
Un condensateur plan est constitué de deux plaques métalliques rectangulaires A et B de longueur L et séparées d'une distance d. Un faisceau de protons est émis en C avec une vitesse nulle et sont accélérés grâce à une tension UCD entre les points C et D par un dispositif non représenté. Les protons pénètrent en un point O équidistant des deux armatures à l'instant t=0 avec une vitesse v0 faisant un angle ß = 30° avec l'horizontale, dans une zone où règne un champ électrique E uniforme entre les armatures planes chargées. On néglige toutes les autres forces s'exerçant sur le système {proton} de masse mP devant la force électrique qu'il subit.

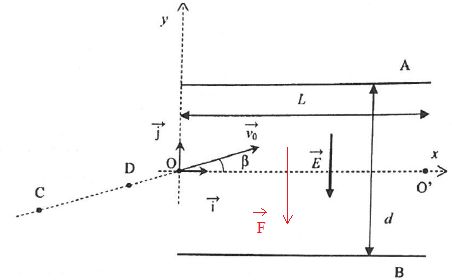
mP = 1,6 10-27 kg ; UCD = 5,0 103 V ; L = 17 cm.
a. Les protons arrivent en O avec une vitesse v0 = 1,0 103 km/s. Vrai.
Travail de la force électrique de C à D : e UCD = 1,6 10-19 *5,0 103 =8,0 10-16 J.
Variation de l'énergie cinétique d'un proton : ½mPv02.
Théorème de l'énergie cinétique : ½mPv02 = 8,0 10-16 .
v02 = 2*8,0 10-16  /1,6 10-27 =1012 ; v0 = 1,0 106 m/s = 1,0 103 km/s.
b. Entre les plaques A et B, la force électrique subie par les protons est dirigée verticalement vers le haut. Faux .
c. Les coordonnées du protons entre les plaques A et B s'expriment par :
x = v0 cos ß t ; y = v0 sin ßt -eE t2 / (2mP). Vrai.
ax = 0 ; ay = eE / mP ; v0x = v0cos ß ; v0y = v0 sin ß.
vx =  v0cos ß ; vy = -eE/mP t +v0 sin ß.
d. Si E = 50 kV m-1, les protons passent en O' ( L ; 0). Vrai.
L = v0 cos ß t ; t = L / (v0 cos ß) ; repport dans y :
y = L tan ß -eE L2 / (2mP v02cos2 ß).
y = 0,17 tan 30 - 1,6 10-19 *5,0 104*0,172 /(2*1,6 10-27 *1012 cos230).
y = 0,17 *0,577 -5*0,172 / 1,5 = 0,17(0,577-0,17 / 0,3) ~0.

Exercice 19.
On considère deux vaisseaux spatiaux V1 et V2 possédant respectivement des horloges H1 et H2 qui ont été initialement synchronisées, auquels on associe les référentiels R1 et R2. Le vaisseau V1 se déplace en ligne droite à vitesse constante v1 = 0,90 c devant le vaisseau V2 qui le suit en ligne droite à la vitesse v2 = 0,10 c par rapport à une étoile très éloignée. Le vaisseau V2 émet en direction de V1 des flashs lumineux toutes les secondes, mesurées sur son horloge H2 au repos dans le référenteil R2.

a. Les ondes lumineuses émises par V2 dépassent V1 à la célérité 0,20 c dans le référentiel R1.
Les ondes lumineuses ont la même célérité dans tous les référentiels galiléens. R1 et R2 sont galiléens.
Les ondes dépassent V1 à la célérité 0,1 c dans R1.
b. La durée propre Dtp entre l'émission de deux flashs lumineux consécutifs vaut une seconde. Vrai.
c. La durée Dt1 qui sépare l'arrivée de deux flashs lumineux, mesurée avec l'horloge H1 est supérieure à la seconde. Vrai.
Le temps s'écoule moins vite dans un vaisseau en mouvement par rapport à un référentiel fixe.
d. Le pilote du vaisseau V1 voit tourner les aiguilles de l'horloge H2 du vaisseau V2 moins vite que celle de son horloge H1. Faux.
Le pilote du vaisseau V2 ne peut pas voir l'horloge H1.

Exercice 20.
On souhaite transmettre une vidéo numérique par un canal de transmission autorisant un débit binaire maximal de 100 Mbits s-1. La vidéo possède les caractéristiques suivantes : 25 images par seconde ; les dimensions de chaque image sont 200 pixels sur 200 pixels ; chaque pixel a été codé sur 10 bits.
La transmission se fait sur une distance de 10 km, sans amplification du signal sur le trajet. Le coefficient d'atténuation linéique a vaut 2 dB km-1.
a. A chaque pixel peut être associé 10 nombres binaires différents. Faux.
210 nombres binaires différents.
b. Le débit binaire admis sur le canal n'est pas suffisant pas pour permettre la transmission de cette vidéo. Faux.
25*200*200*10 =1,0 107 bits s-1 =10 Mbits s-1.
c. L'affaiblissement subit par le signal est de 20 dB. Vrai.
d. La puissance du signal est divisée par 100 lors de cette transmission. Vrai.
A = 10 log (Pémetteur / Précepteur) = 20 ; log (Pémetteur / Précepteur) = 2  ; Pémetteur / Précepteur = 100.

.


  

menu