Niveau sonore. Concours audioprothésiste Nancy 2016. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . .   On définit le niveau sonore en décibel (dB) d'une source sonore comme suit : L =20 log ( Peff / P0) Avec P0=2 10-5 Pa : pression acoustique efficace de référence corespondant à la pression acoustique minimale audible, Peff : Pression acoustique efficace de la source en Pa.' 1. Le niveau sonore de la parole en décibel est de 60 dB à 1 m. A quelle pression acoustique efficace ce niveau sonore correspond-il ? Peff = P0 10L / 20 = 2 10-5 103=2 10-2 Pa. 2. On estime que le seuil de la douleur au niveau du tympan correspond à une pression acoustique efficace de 20 Pa. A quel niveau sonore ce seuil correspond-il ? L =20 log (20 / (2 10-5))=120 dB. 3. De combien augmente le niveau en décibel quand la pression acoustique efficace double ? L' = 20 log (2Peff / P0) ; L = 20 log (Peff / P0) ; L'-L = 20 log 2=6,0 dB. 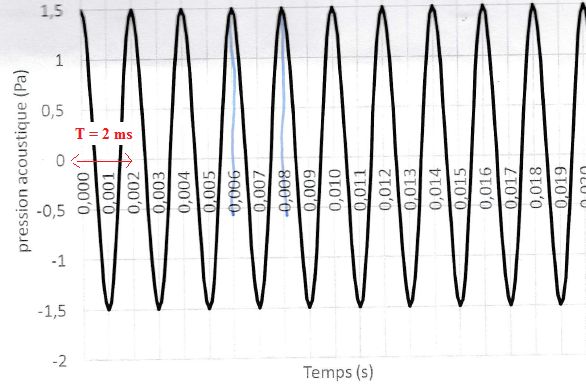La figure suivante représente la variation temporelle de la pression acoustique en un point donné. Cette variation caractérise une onde acoustique sinusoïdale qui se propage. a- Déterminer, pour cette onde sinusoïdale, la période T, la fréquence f et la longueur d.onde . La vitese de propagation d'une onde sonore (célerité) est c : 340 m/s. T est déterminée graphiquement et vaut 2 10-3 s. La fréquence est l'inverse de la période : f = 1 / ( 2 10-3) = 5 102 Hz. Longueur d'onde l = c T = 340 * 2 10-3 = 0,68 m. b-  Calculer le niveau sonore en décibel de l'onde acoustique sinusoidale. Pmax = 1,5 Pa ; Peff = 0,707 Pmax = 0,707 *1,5 =1,06 Pa. L =20 log ( 1,06 / 2 10-5) = 20 log (5,3 10-4)~94 dB. .

menu