Diffraction,
interférences, satellite.
Concours audioprothèsiste Paris 2015.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Partie A :
diffraction de la lumière, expérience de Fresnel.
1. Fresnel a utilisé
les rayons solaires pour réaliser son expérience. En justifiant, dites
quelle va être l'allure de la figure de diffraction obtenue.
La lumière solaire est polychromatique. Chaque radiation donne une
figure de diffraction. Les longueurs d'onde du bleu étant inférieures à
celles du rouge, les taches brillantes sont irrisées de rouge.
2.
Il exploite le phénomène de diffraction de la lumière par un fil de
fer. Le diamètre de ce fil a-t-il une importance pour observer ce
phénomène ? Si oui, quel doit être l'ordre de grandeur de ce diamètre ?
Oui, le phénomène de diffraction est d'autant plus marqué que le
diamètre du fil est plus proche de la longueur
d'onde de la lumière. Longueur d'onde moyenne de la lumière
visible l
= 0,6 µm. Le diamètre du fil doit être de l'ordre de quelques
micromètres.
Partie B :
mesure d'une longueur d'onde par diffraction.
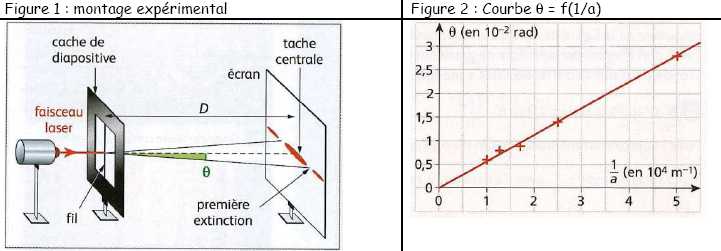
On réalise une expérience de diffraction à l'aide d'un laser émettant
une lumière monochromatique de longueur d'onde l. A
quelques centimètres du laser, on place successivement des fils
verticaux dont on connaît précisément les diamètres qui seront désignés
par a. On observe sur l'écran situé à une distance D= 1,60 m ddu fil
une figure de diffraction. On peut alors mesurer la largeur L de la
tache centrale et calculer la demi-ouverture angulaire q du
faisceau diffracté.
3.
Donner la relation entre L et D qui permet de
calculer q
pour chacun des fils.
tan q
= ½L / D.
Pour les petits angles : q
~ ½L
/ D avec q
en radian.
4. Donner
la relation entre q
et l
ainsi que leurs unités.
q = l /a
avec a et l en mètres.
5. On trace la
courbe q
= f(1/a). Montrer que la courbe obtenue est en accord avec la relation
donnée à la question 4.
La courbe q =
f(1/a) étant une droite passant par l'origine, q et 1/a sont proportionnelles, en
accord avec la relation de la question 4. La constante de
proportionnalité, pente de la courbe, est égale à la longueur d'onde l.
6. Déterminer
graphiquement la longueur d'onde l.
l
= 2,8 10 -2 / (5 10 4) =5,6
10 -7 m.
7. Quelles seraient
les modifications obtenues si on avait remplacé les fils de diamètre a
par des fentes d'épaisseur a ?
On observe la même
figure de diffraction en utilisant un fil de diamètre a ou une fente de
largeur a, dans la mesure où a est du même ordre de grandeur que la
longueur d'onde de la lumière.
|
| .
. |
|
|
Partie C : Mesure d'une longueur
d'onde par interfrences.
On remplace le fil par un écran percé de deux fentes distantes de a =
0,40 mm et on observe des franges sur l'écran placé à D = 3 m des
fentes.

8. Pourquoi la
lumière peut-elle arriver en différents points de l'écran ? Pourquoi
les franges ne sont-elles pas présentes en tout point de l'écran ?
Les deux fentes F1 et F2
se comportent comme deux sources secondaires cohérentes et synchrones.
La figure d'interférences est observable dans la zone de
l'écran où les ondes issues des deux sources secondaires se superposent.
9. A quelle
condition obtient-on une frange brillante ? A quelle condition
obtient-on une frange sombre ? Comment appelle-t-on ces phénomènes ?
Expliquer pourquoi l'intensité de la lumière sur l'écran dépend de la
position y sur l'écran ? Qu'observe-t-on au centre de l'écran pour y =
0 ?
On
observe une frange brillante si la différence de marche est un multiple
de la longueur d'onde. Les interférences sont constructives et
l'intensité lumineuse est maximale.
On observe une frange sombre si la
différence de marche est un multiple impair de la demi-longueur d'onde.
Les interférences sont destructives et l'intensité lumineuse est
minimale.
Au centre de l'écran, les interférences sont constructives (
l'intensité de la lumière est maximale ). De part et d'autre de la
france centrale, on oberve une alternance de franges
brillantes et sombres : l'intensité lumineuse dépend de la
position y sur l'écran.
10.
La largeur sur l'écran d'un ensemble de six franges consécutives est de
25 mm. Quelle est la longueur d'onde du laser utilisé ? Pourquoi mesure
t-on six frange plutôt qu'une seule ?
En mesurant la distance entre six franges consécutives de même nature,
on augmente la précision sur l'interfrange i = lD/a.
25 mm correspond à cinq interfranges : i = 5 mm = 5 10-3
m.
l
= i a / D = 5 10-3 *0,40 10-3
/ 3 ~6,7 10-7 m.
|
|
|
|
Détermination d'une vitesse.
Lors d'une collision survenue sur une autoroute horizontale et
rectiligne, les gendarmes s'interrogent sur la vitesse de l'un des
véhicules accidentés. La masse du véhicule incriminé est m = 1100 kg.
Le rapport de
l'enquète précise deux points :
- la distance de freinage D mesurée à partir des traces des
pneumatiques sur la chaussée est D = 100 m ;
- la force de frottement exercée par la chaussée sur les pneus est
constante pendant le freinage. Sa valeur est f = 6100 N sur route sèche
pour l'ensemble des 4 pneus.
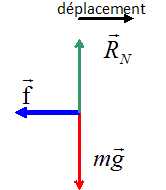
1. Sur un schéma, représenter les forces ( sans
souci d'échelle ) qui s'exercent sur le véhicule pendant le freinage. (
On néglige les frottements de l'air ).
Le véhicule est soumis à son poids, à l'action normale su plan et à la
force de freinage.
3.
En appliquant la loi de la mécanique la plus appropriée mais
que vous énoncerez, déterminer l'expression de la vitesse v au début du
freinage en fonction de m, f et D.
Théorème de l'énergie cinétique : dans un référentiel galiléen, la
variation de l'énergie cinétique du système ( le véhicule ) est égale à
la somme des travaux des forces appliquées au système. Ici, seule f
travaille,le poids et l'action normale du plan étant perpendiculaires
au déplacement.
0-½mv2 = -f D ; v = (2f D / m)½.
3.
Calculer v. Le chauffeur respecte-t-il la vitesse autorisée
de 130 km/h ?
v = (2*6100 *100 / 1100)½ = (1,1 103)½
=33 m /s.
soit 33 *3,6 ~120 km/h. La vitesse autorisée est respectée.
4.
Par temps de pluie ( vitesse limite autorisée 110 km/h ), la vitesse
aurait-elle été respectée ?
Non.
Station
spatiale en orbite.
Par
rapport au référentiel géocentrique, la station ISS effectue 16
révolutions par jour sur une orbite circulaire, inclinée de 21,6 ° par
rapport à l'équateur et située à une altitude h ( environ 400 km ).
Masse de la terre M = 5,97 1024 kg ; rayon de la
terre R =
6380 km ; masse de la station m ; G = 6,67 10-11
SI ;
h = 400 km.
1.
Représenter
sur un schéma la force gravitationnelle que la terre exerce sur la
station puis donner son expression vectorielle.
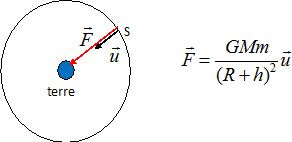
On
suppose que seule la force gravitationnelle s'exerce sur la station.
2.
Montrer que le
mouvement est uniforme et établir l'expression de la vitesse en
fonction des données.
La seconde loi de Newton conduit
à :
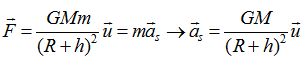
La force de gravitation,
perpendiculaire à la vitesse, ne travaille
pas. En conséquence l'énergie cinétique et la valeur de la vitesse du
satellite ne sont pas modifiées. La valeur de la vitesse étant
constante, le mouvement est uniforme.
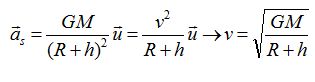
3. La masse m de la
station croît au fur et à mesure de
sa construction.
La
vitesse de la station sur son orbite sera-t-elle modifiée ? Justifier.
La vitesse de la station est indépendante de sa masse. Cette vitesse
restera donc constante.
4. Quelle est la loi
de Kepler qui prévoit que le mouvement circulaire d'un satellite est
uniforme ? L'énoncer..
Deuxième loi ou loi des aires : le
mouvement de chaque planète est tel que le segment de droite reliant le
soleil et la planète balaie des aires
égales pendant
des durées égales.
5. Définir puis
établir l'expression de la période de révolution de la station en
fonction des données.
Durée
(s) nécessaire pour décrire une circonférence ( 2pr en mètre) à la
vitesse v ( m/s) définie ci-dessus.
2pr
= v T ; T=
2pr
/ v avec r = R+h.
Expression de T en fonction de G, M et r :
Elever au carré l'expression de la période : T2 = 4p2 r 2 / v2.
Remplacer v2 par son
expression GM/ r : T2 = 4p2 r 3 / (GM).
T = 2p[r 3 / (GM)]½.
6.
Enoncer la troisième loi de Kepler et montrer qu'elle est vérifiée.
Le carré de la période de révolution est proportionnel au cube du rayon
de l'orbite.
r = (6380+400) 103 =6,78 106
m.
T = 24*3600 / 16 = 5,4 103 s.
T2 / r3 = (5,4 103)2
/ (6,78 106)3 = 9,4 10-14.
4 p2/(GM)
=4*3,142 / (6,67 10-11 *
5,97 1024) =9,9 10-14.
7.
Définir un satellite géostationnaire.
Pour être géostationnaire le satellite doit avoir:
* une trajectoire circulaire de centre O, centre de la Terre
* pour période de révolution celle de de la Terre
*et de plus il doit tourner dans le même sens que la Terre avec le même
axe de rotation
donc le plan de sa trajectoire est perpendiculaire à l’axe de rotation
de la Terre et il contient le point O : le plan de la trajectoire est
obligatoirement équatorial.
8.
La station est-elle géostationnaire ? Justifier.
Non, sa période de révolution n'est pas égale à 24 heures et son orbite
n'est pas dans le plan équatorial.
|
Détermination d'une distance en mer.
Des
scientifiques étudiant les cétacés captent le chant d'une baleine en
pleine mer. Le son est détecté par deux capteurs, un dans l'air,
l'autre dans l'eau. On suppose que la baleine nage juste à la surface
et que le son se propage dans les deux milieux. Le capteur placé
dans l'air reçoit le son avec un retard Dt
= 6,71 s par rapport à celui placé dans l'eau. A quelle distance D des
capteurs se situe la baleine ? Vitesse du son dans l'air v = 340 m/s ;
vitesse du son dans l'eau vE = 1480 m/s.
D = vE tE ; D = v t ; Dt = t-tE = D [ 1 / v -1 / vE] = D[ (vE-v) / (v vE)].
D = Dt v vE / (vE-v) = 6,71 *340*1480 /(1480-340)=2,96 103 m.
|
|