QCM
Mécanique.
Concours audioprothèsiste Bordeaux 2016.
|
|
.
.
|
|
|
|
|
|
|
|
Une
seule réponse juste par question. Des points négatifs seront affectés
en cas de réponses fausses..
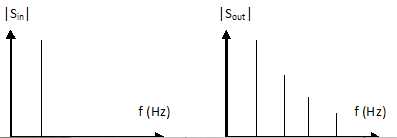
21. Sur la figure
ci-dessous, on observe le spectre d'un signal audio à l'entrée S in
et à la sortie S out d'une pédale d'effet.
 Le
signal d'entrée semble être une impulsion et l'effet de la pédale
pourrait être de type "écho".
Le
signal d'entrée semble être une impulsion et l'effet de la pédale
pourrait être de type "écho".
Le signal
d'entrée semble être un son pur et l'effet de la pédale pourrait être
de type "écho".
Le signal
d'entrée semble être une impulsion et l'effet de la pédale pourrait
être de type "distorsion".
Le signal d'entrée semble être un son pur et
l'effet de la pédale pourrait être de type "distorsion". Vrai.
Le signal d'entrée semble être une impulsion
et l'effet de la pédale pourrait être de type "réverbération".
22.
Afin de numériser un signal sonore,on utilise un microphone relié à une
carte d'acquisition de résolution 8 bits,utilisée sur le calibre [-1 V
; +1 V ]. On enregistre pendant une durée de temps dt = 100 ms et de
manière la plus fidèle possible avec cette carte, un son de fréquence
500 Hz. Quelle est la résolution de cette tension ?
0,00078 V ; 0,0078 V ; 0,078 V ; 0,78 V ; 7,8 V.
2 / 2 8 = 0,0078
V.
23. Un canal de
transmission a un coefficient d'atténuation de 9,0 dB/km. La puissance
mesurée en entrée est de 100 mW et la réception impose que la puissance
de sortie ne soit pas inférieure à 3,5 µW. La longueur maximale ( en
km) de ce canal est : 44,6 ; 401,0 ; 10,0 ; 3,0 ; 5,0.
100 mW = 1,00 10 5 µW ; 1,00 105 / 3,5 = 28571 ;
Atténuation maximale : A = 10 log 28571 = 44,6 dB.
Longueur maximale du canal : 44,6 / 9 ~5,0 km.
24. Un
solide animé d'un mouvement rectiligne possède une vitesse dont la
variation en fonction du temps est représentée par le diagramme
ci-dessous. Quelle est la distance parcourue par le solide entre
l'instant t =0 et t = 4 s. ?:
20 m ; 25 m ; 30 m ; 40 m ; 45 m.
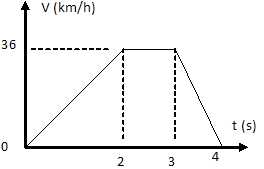
Mettre
la vitesse en m /s : 36 / 3,6 = 10 m/s.
L'aire comprise entre la courbe et l'axe des x donne la distance
parcourue : 10 +10 5 = 25
m.
25.
Un véhicule S 1 de masse 2 t et de
vitesse constante 54 km/h percute un véhicule S 2
de masse 1 t et de vitesse constante 54 km/h. Les deux véhicules ont
des trajectoires perpendiculaires sur un sol glissant avant de
s'accrocher. Le choc a lieu au point C. Quelle est la valeur de l'angle
a
de la direction de l'ensemble des deux véhicules imbriqués après le
choc par rapport à la direction initiale du véhicule S 1
? On suppose les véhicules indéfomables.
31 ° ; 59° ; 37° ; 53° ; 42°.
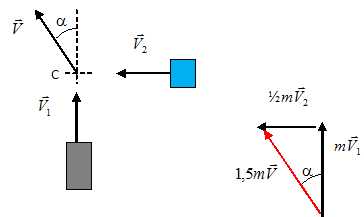 Conservation
du vecteur quantité de mouvement du système isolé constitué par les
deux véhicules.
Conservation
du vecteur quantité de mouvement du système isolé constitué par les
deux véhicules.
tan a
= 0,5V2 / V1 =27 / 45 =
0,60 ; a
= 31°.
26. Un joueur frappe
un ballon de masse 400 g. Quelle est la vitesse du ballon si la vitesse
de la jambe ( de masse 20 kg) varie de 1,5 m/s à 0,75 m/s
après la frappe ?
40 km/h ; 65 km/h ; 110 km/h ; 135 km/h ; 170 km/h.
Les vecteurs quantités de mouvement de la jambe et du ballon sont
colinéaires et de même sens.
Quantité de mouvement du système {jambe
ballon} avant la frappe : 20*1,5 = 30 kg m s-1.
Quantité de
mouvement du système {jambe ballon} après la frappe : 20*0,75 +0,4 v=
15 +0,4 v.
Conservation de la quantité de mouvement : 30 = 15 +0,4 v ;
v = 15 / 0,4 = 37,5 m/s ou 37,5*3,6 = 135 km /h.
27.
Une année lumière vaut :
1015 km ; 1016 m ; 3 108
m ; 3 108 km ; 365 108
m.
Distance parcourue par la lumlère dans le vide en une année :
3 108 *3600*24*365 = 9,46 1015
m ~1016 m.
28.
Lucke et Léia sont deux faux jumeaux. Lucke quite la terre le jour de
ses 30 ans et voyage dans une fusée supposée ponctuelle se déplaçant à
la vitesse v = 0,8 c. Il se dirige vers Sirius qui se situe à
environ 9,0 a l de la terre. On néglige la phase
d'accélération et de décélération de la fusée.
Lucke
observe un pendule dont il mesure la période d'oscillation égale à 2,4
s. Quelle période ( en s ) mesurerait Léa, restée sur terre ? 3,1 ; 1,9
; 4,0 ; 2,4 ; 1,4.
g
= [(1-(v/c)2]-½ =1,67.
Durée propre : 2,4 s ; durée mesurée : 2,4 *1,67 =4,0 s.
|
| .
. |
|
|
29. Pour aborder le
problème du positionnement par mesure du temps,on étudie tout d'abord
le repérage d'un promeneur le long d'une route étroite. Ce repérage
nécessite deux balises fixes émettrices A et B,situées aux extrémités
de la route de longueur AB = D = 300 km. Le signal émis par chaque
balise contient l'heure d'émission du signal. On suppose ici, pour
simplifier, que la vitesse de propagation du signal est v = 10 km /min.
Au point P, le promenur reçoit simultanément un signal de A contenant
l'heure d'émission t0 et un signal de B
contenant lui aussi l'heure à laquelle B a envoyé son signal t0
+ Dt
avec Dt
= 10 min. Les deux balises sont supposées parfaitement synchronisées.
Que vaut la distance PA ?
100 km ; 200 km ; 50 km ; 150 km ; 250 km.
On note x la
distance PA ( en km) et t( en minute) la date de réception
des deux signaux par P.
x = vt = 10 t ; 300-x = v(t-Dt)
=10 (t-10).
t = 0,1 x ; 300-x = 10(0,1x-10) =x-100 ; x = 200 km.
30. Suite de la
question précédente. Lorsque le promeneur reçoit les deux
signaux, sa montre indique tp = 10 h 24 min.
L'heure d'émission des signaux étant connue ( t0
= 10 h05 min, on peut déterminer l'avance oule retard de la montre de P
par rapport aux horloges des balises.
Calculer l'heure théorique que devrait indiquer la montre du promeneur
lorsqu'il reçoit les signaux.
10 h 15 min ; 10 h 26 min ; 10h 24 min ; 10 h 25 min, vrai ; 10 h 23 min.
t = 20 min ; ajouter à t0.
31. Les deux
questions précédentes sous-entendaient que les horloges A et B étaient
synchronysées. Intéressons-nous dans un second temps à la
synchronistion de deux horloges immobiles éloignées d'une distance
inconnue. A l'instant tA 1 ( selon l'horloge
A),l'horloge A émet un signal lumineux vers l'horloge B. Dés réception,
l'horloge B lui envoie un signal contenant son heure de réception tB
2 ( selon l'horloge B) ; l'horloge A reçoit ce second
signal à la date tA 3 ( selon A).
Si tA1 = 10h 00 min, tA 2 = 10 h 07 min et t A 3 = 10 h 10 min, déterminer le retard ( en min ) de l'horloge A sur celle de B. ( 1 ; 2 ; 3 ; 4 ; 5 ).
Durée de l'aller-retour : t A 3 -tA1 =10 min selon A. La durée du trajet est de 5 min.
Arrivée du signal émis par A en B : 10 h 05 min selon A et 10 h07 min selon B.
A retarde de 2 min sur B.
|
|
|
|
32. Dans un cristal,
les tomes sont disposs de manière trs ordonnée selon un réseau
tridimensionnel. Dans ce réseau, il existe des plans privilégiés dits
réticulaires. La distance d entre deux plans réticulaires peut être
déterminée par diffraction des rayons X, dont les longueurs d'onde sont
comprises entre 0,1 nm et 10 nm. La différence de marche entre les
rayons 1 et 2 est :
d sinq
; 2d sin q , vrai ; d / sin q ; d
tan q
; 2d cos q.
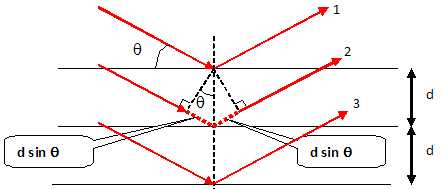
33. Suite
de la question précédente. La
différence de marche entre les rayons 2 et 32 est :
2d cos q
; 4d sin q ; d sin q ; d
tan q
; 2d sin q, vrai
34.
Suite
de la question précédente. La loi de Bragg, qui exprime la
condition d'interférence entre les rayons 1, 2, 3... est :
2d cosq = kl, k
entier. d / sin q
= ½k l
; 2d sinq = kl, vrai ; d sin q =
(2k+1)l
; d tan q
= k l.
35.
Suite. Pour l
= 0,10 nm, le plus petit angle pour lequel on trouve une tache
correspondant à des interférences constructives est 30°. En déduire la
distance d.
k = 1 ; 2 d sin q
= l
; d = 0,10 / (2 sin 30) = 0,10
nm.
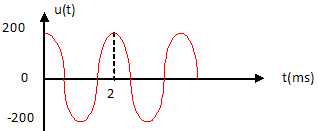
36.
Quelle courbe correspond à l'équation suivante u(t) = 200 cos (1000 p t).
Amplitude : 200 ; période T : 1000 p = 2 p / T
; T = 1/500 = 2 10-3 s = 2 ms.
A t = 0, u(0) = 200. Courbe
C.
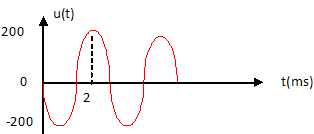
37. Quelle courbe
correspond à l'équation suivante u(t) = 200 cos (1000 p t +½p).
Amplitude : 200 ; période T : 1000 p = 2 p / T
; T = 1/500 = 2 10-3 s = 2 ms.
A t = 0, u(0) = 0. Courbe
D.
38. Un cor des
Alpes, de longueur 3,4 m, émet un son de fréquennce telle que la
longueur d'onde de l'onde émise est égale au double de la longueur de
l'instrument. On rappelle que l'intensité sonore décroît en 1/r2
( où r désigne la distance par rapport à la source. Si le niveau sonore
à 1 m est 100 dB, donnez le niveau sonore à une distance de
8,7 km correspondant au village voisin et indiquez si le cor peut être
entendu dans ce village.
A un mètre : I = k /12 =I0 10L/10 =10-2 W m-2, avec k une constante.
A 8700 m, I' = k / 87002 = 1,32 10-8 k = 1,32 10-10 W m-2.
L = 10 log [1,32 10-10 / 10-12]=21 dB.
Fréquence f = c / l = 340 / 6,8 = 50 Hz.
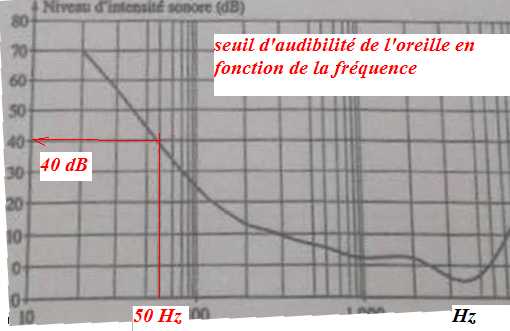
Le cor n'est pas audible.
39. Lors d'une expérience au
LHC du CERN, une des particules émises lors des collisions entre les
protons est le méson B. Sa durée de vie propre est Dt0
= 1,5 ps. Un détecteur repère les mésons B produits dans le référentiel
du laboratoire supposé galiléen et mesure une distance moyenne de
parcours du méson B de 10 mm avant sa disparition. En supposant que la
vitesse du méson B est proche de c, calculer le coefficient de Lorentz
et déduisez-en la vitesse exacte du méson B.
Dt = 0,010 / (3 108)=3,33 10-11 s = 33,3 ps.
g = Dt / Dt0 =33,3 /1,5 =22,22 ~ 22.
22,22 = [1-(v/c)2]-1 ; 1-(v/c)2 = 0,002 ; (v/c)2 =0,998 ; v = 0,999 c. Réponse D.
40.
L'orbite de Hohmann est la trajectoire optimale en termes d'économie
d'énergie pour se rendre d'une planète à une autre. Cette orbite
entre la Terre et Mars est une demi-éllipse de centre O de
demi-grand axe a. Determiner la valeur de a (en km ).
1,89 108 ; 2,19 108 ; 1,79 108 ; 1,98 108 ; 1,19 108.
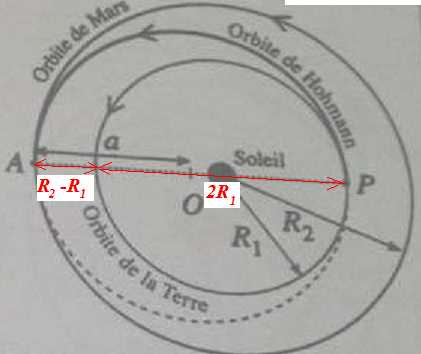
R1 =1,5 108 km ; R2 = 2,3 108 km ; 2 a = R1+R2 ; a = ½(R1+R2) = 0,5 (1,5+2,3) 108 = 1,9 108 km.
|
.41. Par analyse dimensionnelle, retrouvez la troisième loi de Kepler parmi les propositions suivantes.
T2/(GMs) =4p2 /a3 ; T2/ a3 = 4p2 / (GMs) ; T2/ a3 =GMs/ (4p2) ; T2/ a3 = 4p2 / (GM2s).
[T2/ a3 ]= T2 L-3 ; (4p2) st sans dimension ; [G]= L3T -2 M-1 ; [GMs]=L3T -2 ; [1/(GMs)]= T2 L-3 .
42.
En vous aidant de la troisième loi de Kepler, calculer la durée du
voyage ( en jours) du robot Curiosity ( lancé en 2011 ) entre la Terre
et Mars.
518 ; 426 ; 259 ; 213 ; 352.
La
sonde parcourt la moitié de l'ellipse entre A et P. La durée du
parcours est la moitié de la période de révolution T sur l'ellipse. La
troisiéme loi de Kepler donne la période T en fonction de a.
T2 = 4p2 / (GMS) a3.
T = 2*3,14 / [6,7 10-11*2 1030] ½ *(1.9 1011)1,5 =4,5 107 s ; ½T = 2,2 107 s ~260 jours.
43. En vous aidant de la troisième loi de Kepler, déterminer la durée ( en jours ) d'une orbite complète de Mars autour du Soleil.
513 ; 687 ; 312 ; 624 ; 344.
T = 2*3,14 / [6,7 10-11*1,9 1030] ½ *(2,3 1011)1,5 =5,97 107 s ~690 jours.
44. Déduisez-en l'angle a qui repère la position de Mars au sépart afin que Curiosity se rencontrent bien au point d'arrivée.
49° ; 44° ; 51° ; 53° ; 41°.
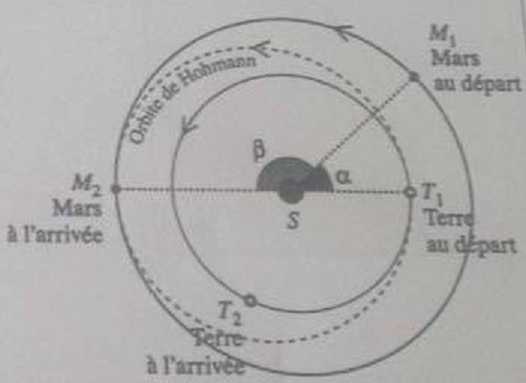
Durée du parcours de Mars : 260 jours ; 690 jours correspondent à 360°.
360*260 / 690 = 136° ; puis 180-136 = 44°.
45.Le son d'une clarinette, enregistré par un microphone est reproduit.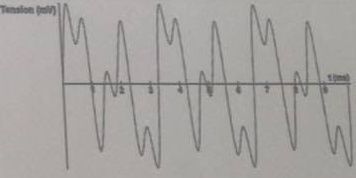
Cette tension est numérisée par un convertisseur analogique numérique
16 bits. La fréquence d'échantillonnage est réglée à 48 kHz. Le débit
binaire en kilobits par seconde (kbps ) du flux aydio associé à cet
enregistrement est : 262 ; 768 ; 12300 ; 49200 ; 48.
48 000 échantillons par seconde avec16 bits chacun : 48*16 = 768 kbps.
46.
On considère une chandelle de rugby dont la trajectoire est représentée
ci-dessous. ( on négligera les effets de l'air ). A t=0 le vecteur
vitesse fait un angle a = 60° avec l'axe Ox et sa valeur est v0 = 10 m/s. Cette trajectoire est caractérisée par les expressions suivantes de x(t) et y(t).
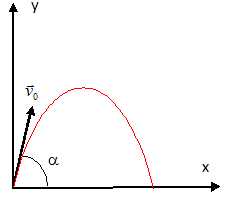
ax = 0 ; ay = -g.
vx = v0 cos a ; vy = -gt +v0 sin a .
x(t) = v0 cos a t ; y(t) = -½gt2 + v0 sin a t. Réponse D.
47. L'équation de la trajectoire de la chandelle est :
t = x /( v0 cos a) ; repport dans y :
y = -½gx2 / ( v0 cos a) 2 + tan a x.Réponse A.
48. Retrouvez, parmi les courbes suivantes, celles qui correspondent à x(t), y(t), vx(t) et vy(t).
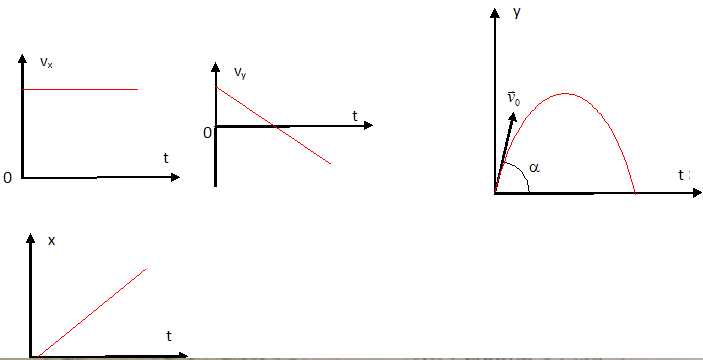
Réponse E. |
|