Effet Doppler et
galaxies, pesée du monde. Concours
audioprothèsiste Paris 2016.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Effet Doppler et galaxies.
Une onde périodique émise par une source avec la fréquence fE
est reçue par un récepteur à la fréquence fR qui n'est pas
nécessairement la même. C'est l'effet Doppler.
On calcule fR par la formule fR = fE[1+
V / c], V étant la vitesse de l'onde dans la direction de l'observateur
( comptée négativement si la source s'éloigne ) et c la célérité
de l'onde ( ici la lumière, c = 3,0 108 m/s ).
La galaxie
NGC 891 est une galaxie spirale, vue sur la tranche, et située à 30
millions d'années de lumière. Ele s'éloigne de nous à la vitesse V =
528 km/s.
Les angles sous lesquels on l'observe dans le ciel sont 3,9 10-3
rad et 0,73 10-3 rad.
1.
La galaxie est photographiée à l'aide d'une lunette astronomique qui la
suit dans son mouvement durant toute la pose, qui dure 76 min.
l'enregistrement s'effectue grâce à un capteur CCD.
La monture de la lunette astronomique, de diamètre 102 mm, se comporte
comme un trou qui limite le passage de l'onde lumineuse.
a) Pourquoi l'image
d'une étoile ponctuelle n'est-elle pas ponctuelle sur le capteur ?
Au
lieu de voir des étoiles ponctuelles à travers un télescope ou une lunette, on voit
des taches. La diffraction brouille les images astronomiques.
b) Quelle est alors l'intérêt de se
procurer une lunette astronomique de diamètre plus important ?
Le rayon de la tache centrale de diffraction est inversement
proportionnel au diamètre de la lunette.
Plus le diamètre de la lunette est grand, plus on peut séparer des
objets proches en distance angulaire.
2.
L'étude du spectre de la lumière de cette galaxie montre des raies
d'absorption de l'hydrogène présent dans les étoiles, dont la raie
Balmer a. Cette
raie a pour longueur d'onde dans le vide lE = 656,3 nm
lorsqu'on étudie le spectre d'une lampe à hydrogène au laboratoire.
a) Pourquoi la position de cette raie n'est-elle pas la même dans le
spectre de la galaxie ?
La fréquence de la lumière reçue est différente de la fréquence émise.
La célérité de la lumière dans le vide étant constante, la longueur
d'onde de la lumière reçue est différente de celle émise.
b) Calculer la fréquence fR, correspondant à cette
raie, dans le spectre de NGC891 visualisé sur terre.
fE = c / lE =3,0 108 / (656,3 10-9) =4,57 1014 Hz.
fR = fE[1+
V / c] = 4,57 1014 [1-528 /(3,0 105] =4,563 1014 Hz.
c) En déduire la longueur d'onde dans le vide lR correspondante.
lR=c / fR = 3,0 108 / (4,563 1014) ~6,57457 10-9 m = 657,5 nm.
d) Comment est modifiée la couleur des objets stellaires de la galaxie ?
On observe un décalage vers le rouge lorsque la galaxie s'éloigne.
e) Dans le catalogue Messier répertoriant les objets célestes connus,
le décalage spectral, défini comme z = (lR-lE) / lE vaut pour cette galaxie 0,00176 ±0,000 01. Est-ce cohérent, sachant que les longueur d'onde sont connues à 0,1 nm près ?
z = (657,457 -656,3) / 656,3 = 1,763 10-3. Le décalage spectral est cohérent.
|
| .
. |
|
|
Pesée du monde.
On admet que la terre et la lune ont chacune une répartition de masse à
symétrie sphérique et que la lune se déplace sur une orbite circulaire
autour de la terre. On appelle r la distance entre les centres des deux
astres.
1.
Faire le schéma de l'orbite de la lune dans le référentiel géocentrique
et représenter la force gravitationnelle exercée par la terre sur la
lune.
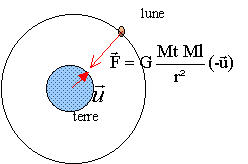
2. L'expression de la valeur F de cette force se met sous la forme F = ML g, ML désignant la masse de la lune.
a. Montrer que g peut s'écrire g = GMT / r2.
F = G MT ML / r2 = ML g, avec g =GMT / d2.
b. Préciser ce que représente chaque lettre figurant dans cette expression.
G : constante de gravitation universelle ; MT : masse de la terre et r distance entre les centres de la terre et de la lune.
c. Etablir l'expression de g en fonction de R ( rayon terrestre ) r et g0, valeur de g au niveau du sol terrestre.
Au niveau du sol terrestre g0 = GMT / R2 soit GMT =g0R2 .
Par suite g = g0R2 / r2.
|
|
|
|
3. Mouvement de la lune.
a. Appliquer la
seconde loi de Newton à la lune dans le référentiel géocentrique
supposé galiléen. Exprimer le vecteur accélération du centre d'inertie
de la lune.
La lune est soumise uniquement à la
force de gravitation de la terre.
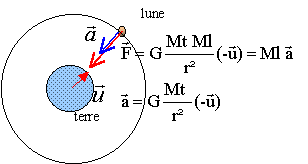
b. Soit V la vitesse de la lune sur son orbite. Donner les
caractéristiques du vecteur accélération du centre de la lune en
mouvement circulaire uniforme.
Le vecteur accélération est dirigé vers
le centre de la terre : a = aN = v2/ r.
c. Montrer que l'expression de g0 est donnée par : g0
= V2 r /R2.
a = g = g0R2/ r2 soit g0=
a r2 / R2 = v2 r / R2.
4. Depuis l'antiquité on sait que r=60 R et que la période de
révolution de la lune est T=27 jours 7 heures 43 minutes. En 1670 Jean
Picard par une méthode de triangulation trouve une valeur de R de 6370
km. En 1686 Isac Newton utilise ces données pour déterminer la valeur
de g0.
Exprimer V en fonction de T et de r ; retrouver la
valeur de g0 déterminée par Newton.
durée mise par la lune pour parcourir
une circonférence de rayon r à vitesse constante v.
2p r = vT ou encore 4p2 r2 = v2
T2
avec v2 = g0 R2/r ; 4p2 r2= g0 R2 T2/r.
g0 = 4p2 r3
/ (R2 T2).
sachant que r=60R : g0 = 4p2(60R)3
/ (R2 T2)=4p2R(60)3 / T2
g0= 8,518 10 6 R
/T 2
R = 6,37 10 6 m ; T = 27*24*3600 + 7*3600 + 43*60 = 2,36 106
s.
g0 =8,518 10 6
*6,37 10 6 / (2,36 106)2= 8,518 * 6,37 / 2,362 =
9,74 m/s².
5. En 1796 Henry Cavendish mesure G à l'aide d'une balance de
torsion. Il obtient G=6,670 10-11 N m² kg-2; g0
étant connu, on peut alors déterminer la masse de la terre.
Déterminer la masse de la terre avec les données suivantes : g0
=9,81 ms-2 et R= 6370 km.
g0 = G Mt /R2 soit Mt = g0 R2 / G.
Mt = 9,8 *(6,37 106)2 /( 6,67 10-11
)= 9,8*6,372 *1023 / 6,67 =5,96 1024
kg .
6. En l'an 2000 deux physiciens de l'université de Washington
améliorent le dispositif de Cavendish et obtiennent une valeur de G
comprise entre 6,674 1 10-11 et 6,674 4 10-11N m²
kg-2;
- pour les physiciens d'aujourd'hui la terre est-elle plus légère ou
plus lourde que pour Cavendish ? Pour répondre on donnera un encadrement de la valeur de la masse de la terre.
Mt = 9,8 *(6,37 106)2 /( 6,6741 10-11
) =5,958 1024
kg.
Mt = 9,8 *(6,37 106)2 /( 6,6744 10-11
) =5,9579 1024
kg .
La valeur de G ( valeur 2000) est un peu supérieure à la
valeur prise par Cavendish.
Dans le calcul précédent G intervient au dénominateur.
Toutes les autres valeurs sont inchangées.
donc Mt , valeur 2000, sera un peu plus petite que la valeur
de Cavendish.
|
|