Mouvements dans
des champs uniformes.
Concours audioprothèsiste Nancy 2015.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Une
balle de golf frappée au sol à l’instant t=0 s est soumise à son poids
seulement. Le mouvement de la balle est suivi dans le référentiel
galiléen terrestre, l’origine O correspond à la position de la balle au
départ de son vol, l’axe (O,z) est vertical vers le haut. On frappe en
utilisant un club incliné d’un angle a, ce qui permet de communiquer à
la balle une vitesse initiale
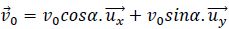
On mesure la portée
du tir, c’est-à-dire la distance D entre O et le point de chute C de la
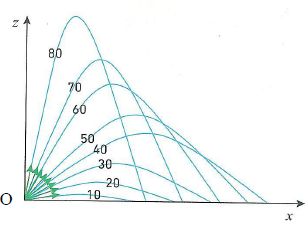
balle sur le sol. On réalise pour cela une série de tirs en faisant
varier a entre 10° et 80°, tous les autres paramètres égaux par
ailleurs. Les résultats sont rassemblés sur la figure.
1)
Rappeler les expressions des équations horaires x(t) et z(t) de la
balle assimilée à un point matériel m soumis à son seul poids : on
notera g la norme de l’accélération de la pesanteur.
x(t) = v0 cos a t.
z(t) = -½gt2 + v0 sin a t.
2) En éliminant t entre les deux équations horaires x(t) et z(t), donner l’expression cartésienne de la trajectoire.
t = x /( v0 cos a ). Repport dans z(t) :
z(t) = -½g x2 / ( v0 cos a )2 +x tan a.
3) Quelle est l’équation vérifiée par la portée D ?
Au sol z = 0 : -½g x2 / ( v0 cos a )2 +x sin a / cos a.
-½g x / ( v02 cos a ) + sin a.
4) La résolution de l’équation de la question 3) donne la solution suivante :
D = v02sin ( 2a) /g.
Pour quelle valeur de a la portée est-elle maximale ? Est-ce cohérent avec le graphique ?
sin ( 2a) = 1 soit a = 45°, cela est cohérent avec la figure ci-dessus.
|
| .
. |
|
|
Services au tennis.
Dans les compétitions de tennis, le service a toujours posé des
problèmes d’arbitrage, en raison de la vitesse à laquelle se trouve
propulsée la balle lors de cette mise en jeu. Depuis les années 1970,
de nombreux inventeurs se sont donc démenés pour fournir aux arbitres
un juge de ligne « électronique », plus fiable que l’être humain. Le
système Cyclops, permettant de détecter si un service est trop long, a
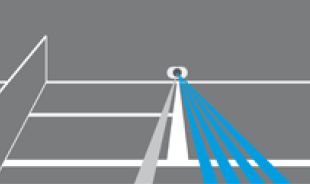
été utilisé sur la plupart des tournois internationaux de 1980 à 2007 :
il est composé de 5 faisceaux lasers et de 5 récepteurs de lumière
situés en face de ces faisceaux, de l’autre côté du court de tennis.
1) La longueur d’onde des faisceaux laser est l = 850 nm. À quel domaine appartiennent les ondes électromagnétiques utilisées par le système Cyclops ?
Domaine infrarouge.
2) Calculer la fréquence de ces rayonnements.
f = c / l = 3,00 108 / (850 10-9)=3,53 1014 Hz.
3) À quelle condition un objet placé sur le trajet de l’un de ces faisceaux risque-t-il d’engendrer un phénomène de diffraction ?
L'objet doit avoir des dimensions du même ordre de grandeur que la longueur d'onde du laser.
4) Sachant que la
diffraction de l’un des faisceaux rendrait le système inopérant,
expliquer pourquoi on a fixé la valeur de la longueur d’onde de façon à
ce qu’elle soit la plus basse possible.
La lumière ne doit pas être visible ; de plus il est peu probable qu'un
objet ( situé 1 cm au dessus du sol) de dimensions de l'ordre du
micromètre se trouve sur le faisceau. Avec une longueur d'onde
plus élevée, de petits insectes pouraient provoquer la diffraction et
perturber le faisceau.
|
|
|
|
Lorsqu’un
service est trop long, il passe devant l’un des faisceaux situés après
la ligne, ce qui déclenche un bip sonore reproduit par un haut-parleur
sur le court afin de prévenir l’arbitre qu’une faute a été détectée.
Voici sur la figure suivante l’enregistrement de ce son ainsi que son
analyse spectrale.
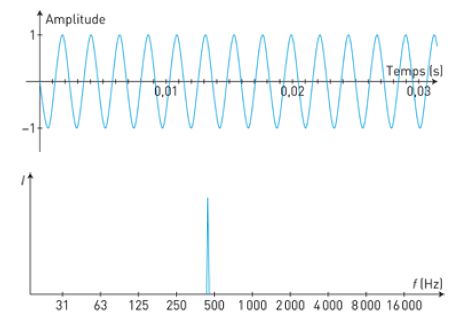
5) a. Déterminer aussi précisément que possible la fréquence de ce son.
11 périodes sont égales à 0,025 s ; T =0,025 /11 ; f = 1 / T = 11/0,025 =440 Hz.
b. La note appelée do1,
jouée sur un piano par exemple, a une fréquence de 261,6 Hz. Le son
produit lors d’une faute de service est-il plus grave ou plus aigu ?
Plus la fréquence est élevée, plus la son est aigu. Le son produit par une faute de service est plus aigu que celle du do1.
c. Est-ce un son pur ? Justifier.
Le spectre compte une seule harmonique ; le signal est sinusoïdal : il s'agit d'un son pur.
Afin de satisfaire un public toujours plus en recherche de statistiques
et de records, des « radars de service », fonctionnant grâce à l’effet
Doppler, sont installés sur de nombreux court de tennis, à 10 mètres
derrière le joueur qui effectue son service. L’onde radio émise par ces
radars a une fréquence f = 34,705 GHz.
6) a. À partir du
moment où le radar détecte la balle en mouvement au-dessus de la tête
du serveur, combien de temps faut-il avant que l’onde envoyée lui
revienne après réflexion sur la balle ? (On considérera que la balle
reste au-dessus du serveur pendant cette phase.)
Le faisceau parcourt 20 m à la célérité c = 3,00 108 ms : 20 / (3,00 108) ~ 6,7 10-8 s.
b. La vitesse de la balle est-elle dirigée dans le même sens que la vitesse de l’onde écho reçue par le radar ?
La vitesse de la balle est dirigée en sens contraire de la vitesse de l'onde réfléchie.
c. On note v la vitesse de la balle et f ’ la fréquence de l’onde écho émise par la balle par réflexion de l’onde radar. f ' = f -D.
Montrer que D = f [1 -(c-v) / c]
f ' = f c /(c+v) = f -D ; D = f -f c /(c+v) = f [1-c /(c+v)] = f v / ( c+v) ~f v / c.
d. Ivo Karlovic détient le record du monde de vitesse au service depuis mars 2011 : 251 km.h-1. Avec quelle variation de fréquence D la balle a-t-elle réfléchi l’onde radar lors de ce service ? Célérité de la lumière : c=2,9979 x 108 m.s-1.
251 /3,6 = 69,7 m /s.
D = f [1 -(c-v) / c] = 34,705 109 |1-(2,9979 x 108-69,7) / (2,9979 x 108)]=8,07 103 Hz.
e. Ivo Karlovic
détient également le record du monde de vitesse lors d’un second
service : l’onde radar a alors été réfléchie avec une variation de
fréquence D = 7428,3 Hz . À quelle vitesse avait-il servi ?
v = Dc / f = 7428,3 *2,9979 x 108/ (34,705 109) =64,17 m/s ou 64,17*3,6 =231,0 km/h.
|
|