Mathématiques
Concours audioprothésiste Bordeaux 2015.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Exercice 1.
1. L'équation
z3-1=0 admet dans R :
A. trois solutions distinctes dans C, vrai ; B. trois solutions distinctes dans R ; C. aucune solution dans R ; D. aucune solution dans C.
E. aucune des propositions
précédentes..
z3=1 ; solution évidente z = 1.
(z-1)(az2+bz+c)=0.
On développe et on identifie les termes : az3-az2+bz2-bz+cz-c=z3-1 ; a =b=c=1 ;
Solutions dans C de : z2+z+1=0 ; D = 1-4 = -3 = 3i2.
z = (-1± i 3½) / 2.
Exercice 2. L'écriture exponentielle du nombre complexe suivant est ::
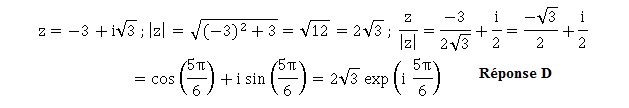
3. L'écriture algébrique du nombre complexe suivant est :
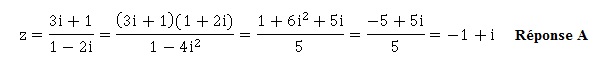
Exercice 3. On considère les nombres complexes z1 = 3 exp(ip/10) et z2 = -3 exp(-ip/10).
4. z15 est :
A. un réel strictement positif, vrai ; B. un réel strictement négatif;
C. un
imaginaire pur
de partie imaginaire strictement positive
;
D. un
imaginaire pur
de partie imaginaire strictement négative ;
E.aucune des propositions
précédentes.
35 exp(ip/10 x5) =35 exp(2 i p) = 35.
5. z25 est :
A. un réel strictement positif ; B. un réel strictement négatif, vrai ;
C. un
imaginaire pur
de partie imaginaire strictement positive
;
D. un
imaginaire pur
de partie imaginaire strictement négative ;
E.aucune des propositions
précédentes.
(-3)5 exp(-ip/10 x5) = -35 exp(-2 i p) = - 35.
6. z250 est :
A. un réel strictement positif ; B. un réel strictement négatif, vrai ;
C. un
imaginaire pur
de partie imaginaire strictement positive
;
D. un
imaginaire pur
de partie imaginaire strictement négative ;
E.aucune des propositions
précédentes.
(-3)50 exp(-ip/10 x50) = 350 exp(-5 i p) = 350 exp(- i p)= - 350.
7. L'argument de z2 est :
A. p/10 ; B. -p/10. C. -9p/10 ; D. 9p/10, vrai. E. 11p/10.
3i2 exp(-ip/10) =3exp(ip) exp(-ip/10) =3exp(-ip/10+ip)=3 exp(i9p/10).
8.L'argument de (z1/z2) est :
A. 1 ; B.0. C. p/10 ; D. p/5, vrai. E. -4p/5. Vrai.
p/10-9p/10= -8p/10= -4p/5.
Exercice 4.
9. 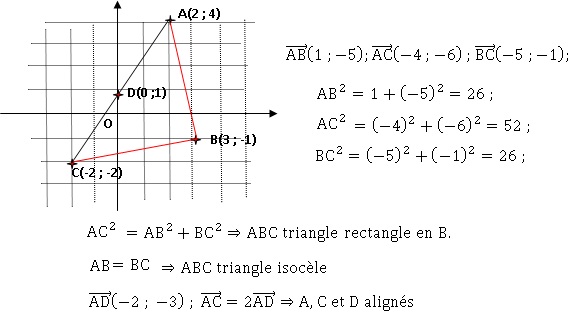
Réponse B.
|
| .
. |
|
|
10. Le Point D apparteint au segment :
A. [AB] ; B. [AC], vrai. C. [BC] ; D. [AO]. E. aucune des propositions
précédentes.
11. Le triangle BCD
est :
A.rectangle en C. B. rectangle en B.
C. isocèle en B.
D. isocèle en D,
vrai ; E. équilatéral.
DC2 =(-2)2+(-3)2 = 13 ; DB2 =32+(-2)2 = 13.
Exercice 5.
12. La valeur de l'intégrale suivante est :
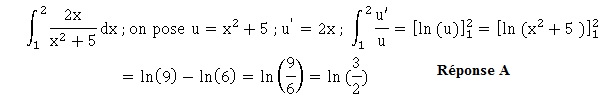
Exercice 6. On donne ln(2) ~0,7 ; e2~7,4.
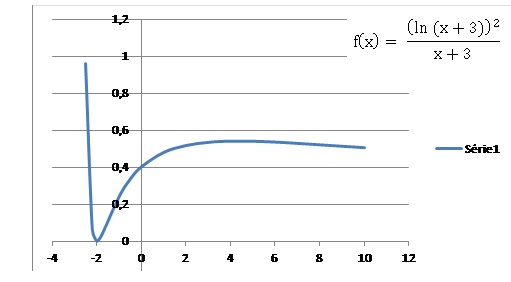
13. L'ensemble de définition de f
est
A. ]-oo ; -3[ union ]3 ; +oo[; B. R-{-3 ; 3} ;
C. [-3 ; +oo[; D. ]- 2; +oo[ ; E. ]-3 ; +oo[, vrai.
14. La limite en +oo de f est :
A. +oo ; B. -oo ;C. 0 Vrai; D. 1 ;
E. aucune des propositions
précédentes.
Par croissance comparée, la fonction puissance croît plus vite que le logarithme au voisinage de l'infiin.
15. La limite en -oo de f est :
A. +oo ; B. -oo ;C. 0 ; D. 1 ;
E. aucune des propositions
précédentes. Vrai.
La fonction n'est pas définie en -oo.
16. Sur son ensemble de définition f est :
A. strictement
croissante ; B. strictement décroissante ;
C. constante.
D. non
monotone, vrai ;E aucune des propositions
précédentes.
17. Sur [-2 ; 1] f
est :
A. strictement
croissante, vrai ; B. strictement décroissante ;
C. constante.
D. non
monotone ; E aucune des propositions
précédentes.
|
|
|
|
18. 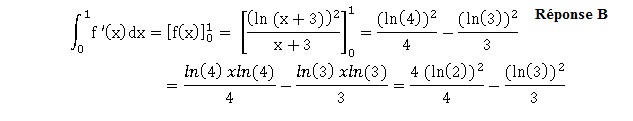
19.
Sur l'ensemble de définition de f, une des primitives F de f a pour expression ::
A. (ln(x+3))3
;
on dérive en posant u = ln(x+3) ; u' = 1/(x+3) ; F = u3 ; F' = 3u2u'=3 (ln(x+3))2 /(x+3)=3 f(x)
B. (ln(x+3))3
; C. 1/3 (ln(x+3))3 *ln(x+3) ;
D. 1/3(ln(x+3))3 vrai ; E. 2ln(x+3).
Exercice 7.
g(x) = sin (4x +p/4)
20. La fonction g est :
A. impaire
; B. paire ;
C.parfois paire, parfois impaire ;
D. ni paire, ni impaire, vrai ; E. à la fois paire et impaire.
21. La fonction g est :
A. non périodique
; B. périodique de période 2p
; C. périodique de période 8p
D. périodique de période 0.25p ; E. périodique de période 0,5p ; vrai.
22. La limite en +oo de g(x) :
A. n'existe pas vrai ; B. vaut zéro; C. vaut 2-½ ;
D. vaut +oo ; E. vaut -oo.
23.
La
limite en +oo de g(1/x) :
A. n'existe pas
; B. vaut 0;
C. vaut 2-½ , vrai ;
D.vaut +oo ; E. vaut -oo.
La
limite en +oo de g(1/x) est égale à la limite en 0 de g(x) soit sin 45 =2½ / 2.
24. Pour tout réel x, la dérivée de g(x) est définie par :
A. cos(4x)
; B. -4 cos(4x);
C. 4 cos (4x +p/4), vrai ;
D.0,25 cos (4x +p/4)
; E. -4cos (4x +p/4).
25. Pour tout réel x, la primitive G de la fonction g, vérifiant G(0)=0 est :
A. -0,25 cos (4x +p/4)
.
B. 0,25 cos (4x +p/4)-2½/8 ; C. -4cos (4x +p/4).
D. -4cos (4x +p/4)+ 2 racine carrée (2). E. aucune
des propositions précédentes.
Vrai.
G(x) = -0,25 cos (4x +p/4)+ Cste ; G(0 ) = -0,25 cos 45 +Cste = 0 ; Cste = cos 45 / 4 =+2½/8.
Exercice 8. h(x) = -5x -6 cos (x/3).
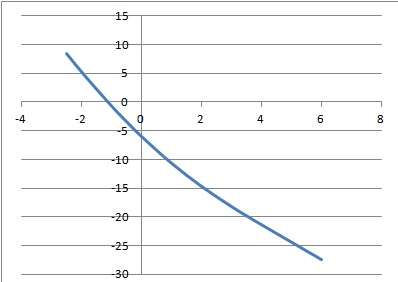
26. La limite en +oo de h(x) est égale
à :
A. +oo.
B.
-oo.Vrai C. 0. D. 1. E. aucune
des propositions précédentes.
Le terme en cosinus est compris entre -1 et 1, négligeable devant -5x au voisinage de l'infini.
27. Pour tout x réel, on a h'(x) =
A. -5-6 sin (x/3)
B. -5+6 sin (x/3). C. -5-2 sin (x/3). D. -5+2 sin (x/3), vrai. E. aucune
des propositions précédentes.
28. Le nombre de solution(s) sur R de h(x)=0 est :
A. 0.
B. 1, Vrai. C. 2. D. infini. E. aucune
des propositions précédentes.
29. La plus grande des solutions de h(x)=0 :
A. est nulle.
B. est strictement positive. C. est strictement négative, vrai. D. n'existe pas.
E. aucune
des propositions précédentes.
Exercice 9.
Soit X une variable aléatoire suivant une loi normale de moyenne -2 et d'écart type s telle que P(X>0)=a.
30. Alors :
A.a=0 ; B. a=0,5 ;
C. a <0,5, vrai ;.D. a >0,5 ; E aucune
des propositions précédentes..
31. P(X<-1) -PX(>1) :
A. n'existe pas ; B. est strictement négative
; C. est strictement positive Vrai..
D. est nulle ;E aucune
des propositions précédentes.
32. P(X< -3)-P(X >-1) :
A. n'existe pas ; B. est strictement négative
; C. est strictement positive .
D. est nulle Vrai ;E aucune
des propositions précédentes.
-1 et -3 sont symétriques par rapport à la moyenne m = -2.
33. P(X= -1) :
A. =0,5 ; B. =0, vrai
; C. =a .D. -0,5 ; E aucune
des propositions précédentes
34.P(X> -2) :
A. =0,5, vrai ; B. =0 ;
C. =a. D. =-0,5 ; E aucune
des propositions précédentes.
|
|
|
|