Puissance sonore,
oscillateur, ondes sonores.
Concours audioprothèsiste Nancy 2015.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
I –
Puissance sonore.
L’onde sonore peut être produite par les vibrations d’une membrane.
Celle-ci provoque des variations de la pression P de l’air qui se
propage. Au repos, la pression de l’air vaut P0 = 1,013×105
Pascal (Pa). On note p1=P-P0 la surpression de
l’air. On a donc P=P0+p1.
Lorsque l’onde affecte le tympan, celui-ci se déforme sous l’action des
forces de surpression et vibre à son tour. L’oreille interne transforme
ces vibrations en un influx nerveux que le cerveau interprète.
Dans le cas particulier des sons purs, à la température de 27°C et sous
des conditions que nous ne préciserons pas ici, la puissance surfacique
moyenne PS (appelée aussi intensité acoustique) du son
exprimée en W/m2 est liée à la
surpression maximale de l’air p1m par la relation :
PS = p21m / (2r0c)
où r0=1,178
kg/m3 représente la densié volumique de l’air et c=347 m/s
la vitesse du son (célérité du son). On rappelle que la définition du
niveau d’intensité acoustique :
LI =10 log[PS / 10-12].
1. On note T la température absolue
de l’air exprimée en Kelvins (K). On démontre que la célérité du son c est
proportionnelle à T½ et que la masse volumique moyenne r0 est proportionnelle à 1/T.
Montrer que PS est
proportionnel à T½ et à p21m.
En
déduire que pour être bien entendu, un son pur doit être émis avec des
surpressions plus importantes quand il fait froid.
c = A T½ et r0 = B / T , r0
c=
AB T -½ avec A et B des
constantes.
PS = p21m
/ (2ABT
-½) =
p21m T ½/
(2AB).
Quand il fait froid, T et en conséquence PS diminuent. Afin
que le niveau sonore reste identique, il faut que PS
augmente.
2.
Le minimum d’audibilité pour l’oreille humaine correspond à un niveau
d’intensité acoustique nul. Calculer la puissance surfacique PS0
et la surpression maximale p10 associées.
LI =0 soit PS0 =1,0
10-12 W m-2.
p210 = PS0(2r0c) = 1,0 10-12
*2*1,178 *347=8,175 10-10 ;
p10 =2,86 10-5 ~2,9
10-5 Pa.
3. La
force maximale exercée sur le tympan de surface S=1 cm2 vaut
fm = S p1m. Calculer la force f0
associée au minimum d’audibilité.
f0 = Sp10 = 10-4
*2,86 10-5
= 2,86 10-9 ~ 3 10-9 N.
4. Le seuil de la douleur est L'1=130
dB. Calculer la force maximale associée f 'm.
LI =10 log[PS / 10-12].
P'S = 10-12
*100,1L'1 =10-12 *1013 = 10 W m-2.
p'21
= P'S(2r0c) = 10
*2*1,178 *347=8,175 103 ;
p'1 =90,4 ~91 Pa
f
' m = 10-2 *90,4 = 0,904 ~0,9 N.
5.
Dans un son pur de fréquence F et de surpression maximale p1m,
la pression varie F fois par seconde entre P0-p1m
et P0+p1m. Justifier que p1m
ne peut en aucun cas dépasser P0. Dans le cas extrême où P0 = p1m,
la puissance surfacique moyenne PS est remplacée par une
puissance surfacique pic PSpic =p21m /(r0c).
Vérifier que le niveau d’intensité sonore pic vaut 194 dB. Que se
passerait-il dans une voiture si ce niveau sonore était atteint ?
Si p1 m dépassait P0 alors P0-p1m
serait négatif ; une pression ne peut pas être négative.
PSpic
=(1,013 105)2 / (1,178*347)=2,51 107
Pa.
L =10 log[2,51 107 / 10-12] =194 dB.
Il en résulterait des dégats irréversibles pour l'audition.
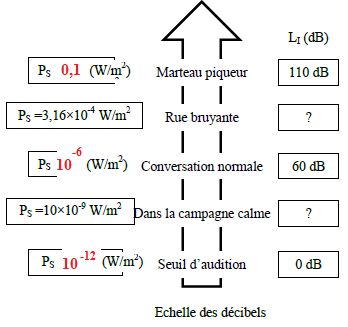
6. Recopier et
compléter sur votre copie l’échelle des décibels de la figure.
|
| .
. |
|
|
II – Amortissement d’un oscillateur.
Première partie.
Lorsqu’un oscillateur élastique est faiblement amorti par une force de
frottement proportionnelle à la vitesse, les oscillations sont
pseudopériodiques et on démontre que :
- La pseudopériode est très proche de la période propre T0 =
2p (m/k)½.
- L’amplitude des oscillations décroit à chaque oscillation selon une
loi géométrique de raison q<1.
Pour
vérifier ces deux lois, on réalise un oscillateur élastique avec un
ressort de raideur k=100 N/m et un mobile M de masse m=2,5 kg
coulissant sur une tige horizontale. On note x = 0 l’abscisse de M
lorsque que le ressort est à sa longueur à vide. On mesure l’évolution
de x en fonction du temps par un dispositif informatique d’acquisition
et on reproduit sur la figure la courbe représentative de la
fonction x(t).
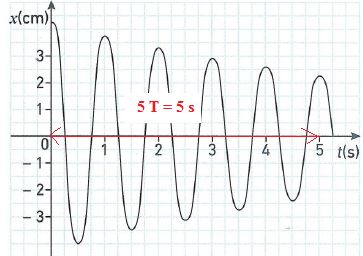
1) Mesurer la
pseudopériode T le plus précisément possible.
T = 1 s.
2) Comparer la
pseudopériode T mesurée et la période propre T0 calculée.
L’écart est-il nul ? inférieur à 0,1% ?, inférieur à 1%, inférieur à 5
% ?
T0 = 6,28 (2,5 /100)½ =0,993 ~0,99 s. L'écart relatif est de 1 %.
3) Justifier que la
vitesse initiale du mobile est nulle à l’instant t=0 s.
L'amplitude initiale est maximale à la date t=0, l'énergie mécanique
est donc sous forme potentielle élastique. L'énergie cinétique initiale
et donc la vitesse initiale sont nulles.
4) Mesurer les
élongations maximales (exprimées en cm) xn du mobile aux
dates t=nT : x0=x(0), x1=x(T), x2=x(2T),…
x5=x(5T). Calculer ensuite le logarithme népérien de chacune
de ces valeurs. Reporter ces valeurs dans un tableau.
x(
cm)
|
4,05
|
3,53
|
3,18
|
2,73
|
2,47
|
2,21
|
ln(x)
|
1,40
|
1,26
|
1,16
|
1,02
|
0,90
|
0,79
|
| ln
q = [ln(xn)
- ln(x0)] / n |
XXXX
|
-0,14
|
-0,12
|
-0,126
|
0,125
|
0,122
|
q
|
XXXX
|
0,87
|
0,89
|
0,88
|
0,88
|
0,88
|
5) Si la suite xn
est une suite géométrique de premier terme x0 et de raison
q, montrer que ln(xn) = ln(x0)+n
ln(q). La loi de décroissance de l’amplitude des oscillations donnée
dans l’énoncé est-elle vérifiée ? Préciser la valeur numérique de q.
xn = x0 qn ; ln(xn) = ln(x0)+n
ln(q).
L'hypothèse d'une suite géométrique de raison inférieure à 1 est
vérifiée.
6)
Le logiciel de repérage du mouvement du mobile ne peut détecter une
élongation inférieure à a=0,2 cm. Estimer le nombre total n
d’oscillations jusqu’à ce que xn = a et la date T à laquelle
les oscillations ne seront plus détectables par le logiciel.
n = [ ln(xn) - ln(x0) ] /
ln q = (ln0,2-1,40) / (-0,125) =24.
T = 24 s.
7)
Cet oscillateur forme-t-il une horloge ?
Cet oscillateur, non entretenu, ne peut pas constituer une horloge.
|
|
|
|
Deuxième partie.
On étudie les oscillations du même dispositif plongé dans de l’eau. On
admet que la valeur de la force de frottement fluide est alors
proportionnelle à la norme du vecteur vitesse f = av où a
est un coefficient constant indépendant de la vitesse et de l’amplitude
du mouvement, ne dépendant que de la forme du mobile M. On effectue des
essais d’oscillations en faisant varier la masse m de M et en
conservant le ressort de raideur k. On réalise 4 expériences avec
m1=2 kg, m2=1,5 kg, m3=1 kg, m4=0,5
kg
Des considérations théoriques conduisent à affirmer qu’on observe :
- un régime d’oscillations amorties quand le facteur de qualité Q = (km)½ / a est supérieur à 0,5.
- un régime sans oscillations quand Q<0,5.
8) Déterminer
l’unité de a et
vérifier que Q est sans dimension.
a est
une force ( N ou kg m s-2 ) divisé par une vitesse ( m s-1).
a
s'exprime en kg s-1 ( M T -1).
k est une force divisée par une distance ; k s'exprime en N m-1
ou en kg s-2.
(k m )½ s'exprime en kg s-1 ; Q est donc sans
dimension.
9) En supposant que
le régime d’oscillations amorties n’apparait
uniquement que dans les cas des masses m1 et m2,
estimer la valeur de a.
Oscillations amorties : (km)½ / a > 0,5 ; a < 2(km)½ ; a < 2(100*1,5)½
; a < 24 kg s-1.
Pas d'oscillation : (km)½
/ a < 0,5 ; a
> 2(km)½ ; a > 2(100*1)½
; a > 20 kg s-1.
III - Ondes sonores
1. Préliminaires.
a) Définir de
manière complète une onde mécanique progressive.
Une onde mécanique est la propagation d'une perturbation dans un milieu
matériel, sans transport de matière, mais avec transport d'énergie.
b) Recopier le
tableau n°1 sur votre copie et complétez les cases vides avec les
expressions suivantes :
Onde sonore, onde le long d’une corde, onde lors de la
compression-dilatation d’un ressort, onde à la surface de l’eau.
|
Onde
à une dimension
|
Onde
à deux dimensions
|
Onde
à trois dimensions
|
Onde
longitudinale
|
Onde
lors de la compression-dilatation
d’un ressort |
|
Onde
sonore
|
Onde
transversale
|
Onde
le long d'une corde
|
Onde
à la surface de l’eau. |
|
2. Mesure de la célérité d’une onde.
On dispose de deux microphones M1 et M2 à la même
distance d d’un diapason. On obtient les courbes représentées sur la
figure n°3. On remarque que les signaux sont en phase.
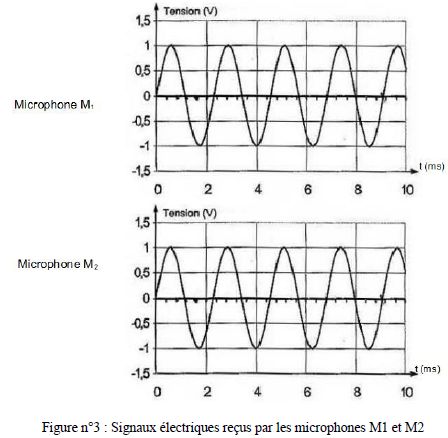
a) Déterminer la
période puis la fréquence du son émis par le diapason.
3 périodes correspondent à 10,1 cm et 6 millisecondes correspondent à
8,8 cm.
T = 2,30 ms et f = 1 / (2,30 10-3)
=434 Hz.
On éloigne le microphone M2 peu à peu jusqu’à ce que les
courbes soient de nouveau en phase. On réitère l’opération jusqu’à
compter cinq positions pour lesquelles les courbes sont à nouveau en
phase. La distance D entre les deux microphones est alors égale à 3,86
m.
b) Pourquoi
compte-t-on plusieurs retours de phase plutôt qu’un seul ?
En comptant un grand nombre de retour de phase, on améliore la
précision sur la longueur d'onde.
c) Définir la
longueur d’onde. Déduire sa valeur numérique de l’expérience précédente.
La longueur d'onde est la distance parcourue par le front d'onde en une
période.
4 l = 3,86 ; l = 0,965 m.
d) Calculer alors
la célérité de l’onde.
c = l f =0,965
*434 = 419 m /s.
e) D’après les
résultats expérimentaux obtenus à la question 2.d), le milieu de
propagation des ondes sonores est-il dispersif ?
L'air n'est pas dispersif pour les ondes sonores.
3. Autre propriété des
ondes sonores.
Lors d’un concert donné par des musiciens dans une salle, des
spectateurs arrivés un peu retard s’étonnent d’entendre de la musique
alors qu’ils sont encore dans le hall et donc séparés de la scène par
un mur très bien isolé phoniquement. Ils remarquent cependant que la
porte, d’une largeur de 1 m, est ouverte. La situation est représentée
sur la figure n°4.

a) Quel phénomène
physique permet d’expliquer l’observation faite par les spectateurs ?
La diffraction des ondes par
la porte, dont les dimensions sont du même ordre de grandeur que la
longueur d'onde.
b) Les spectateurs
ont-ils entendu préférentiellement dans le hall des sons graves (f =
100 Hz) ou des sons très aigus (f = 10000 Hz) ? Justifier la réponse en
calculant les longueurs d’onde correspondantes.
f = 100 Hz : l =
c / f = 419 /100 ~ 4,2 m.
f = 10000 Hz : l
= c / f = 419 /10000 ~ 4,2 cm.
La diffraction est plus marquée pour les sons graves.
|
|
|
VI – Stockage numérique du signal sonore
Partie 1. Conversion
Analogique-Numérique.
Quand on frappe un diapason, il émet un « La » : ses deux branches
vibrent pendant quelques secondes à la fréquence f = 440 Hz, entraînant
la vibration de l’air qui les entoure. Si on place devant le diapason
un micro, la membrane de ce dernier vibre également et ce mouvement est
converti en une tension électrique de même fréquence que le son.
1) Le signal
électrique à la sortie du micro est un signal analogique. Justifier
brièvement cette affirmation.
Le signal électrique est analogique à la sortie du micro, toutes les
valeurs de la tension sont possibles.
2) Un ordinateur ne peut traiter que
des signaux numériques. Définir ce qu’est un signal numérique.
Signal
numérique : la courbe est un ensemble de fonctions constantes par
intervalle, seules quelques valeurs sont possibles.
Pour
traiter un son à l’aide d’un ordinateur (graver un CD par exemple), il
faut convertir le signal analogique obtenu à la sortie du micro en
signal numérique : c’est le rôle d’un convertisseur
analogique-numérique (CAN). On peut décomposer la conversion en deux
étapes : l’échantillonnage et la numérisation. Dans la pratique, ces
deux étapes se font simultanément.
3) Que signifie «
échantillonner » un signal analogique ?
Echantillooer un signal analogique consiste à capturer des valeurs à
intervalle régulier puis à transmettre celles-ci.
4) Combien de valeurs peut prendre
un échantillon numérisé sur 8 bits ?
28 = 256 valeurs.
5) Dans le cas d’un
CD audio, la numérisation se fait sur 2 × 16 bits (stéréo) avec une
fréquence d’échantillonnage de 44,1 kHz. Quelle est, en Mo, la place
théorique occupée sur un CD par une minute de musique non compressée ?
Rappels : 1 octet = 8 bits ; 1 Mio = 220 octets.
Période de
l'échantillonnage : 1 / (44,1 103) = 2,268 10-5 s.
Nombre de valeurs obtenues en une minute : 60 / (2,268 10-5) =2,646 106.
Chaque valeur est codée sur 2*16 bits soit 4 octets.
Nombre d'octets : 4*2,646 106 =1,058
107 soit 1,058 107 / 220 ~
10 Mio.
Lecture d'informations.
Le
CD est en polycarbonate ( matière plastique transparente ) recouvert
d'une couche métallique réfléchissante ( aluminium en général ) elle
même protégée par un vernis. La face supérieure peut être imprimée ou
recouverte d'une étiquette. Les
informations sont stockées sous forme de plats ou de cuvettes sur
une spirale qui commence sur le bord intérieur d'un CD et finit sur le
bord extéroeir. Les creux ont une profondeur de 0,126 µm et une largeur
de 0,67 µm.
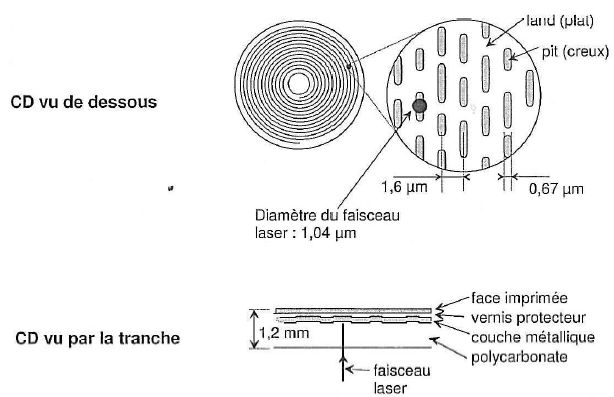
La tête de lecture est constituée d'une
diode laser émettant une radiation de longueur d'onde dans le vide l0
= 780 nm et d'une photodiode détectant la lumière réfléchie par la
surface métallisée du CD. La
lumière émise par la diode traverse une lame semi-réfléchissante avant
de se réfléchir sur un miroir. La lentille assure la mise au point du
faisceau sur le disque. L'ensemble miroir lentille est monté sur un
chariot mobile qui permet au faisceau laser de balayer un rayon du
disque. La surface du disque défile devant le faisceau laser à une
vitesse de 1,2 m/s quelle que soit la position du faisceau.
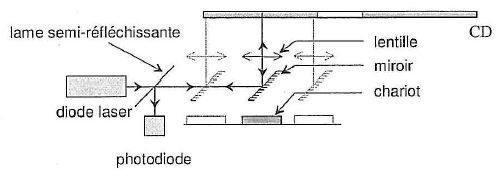
Le codage de
l'information est réalisé par les transitions plat-creux ou l'absence
de transition. On donne c = 3,00 108
m/s ; l'indice d'un milieu transparent est défini par la relation n = c
/ v, v étant la célérité de la lumière dans le milieu transparent.
1) Citer une propriété du laser
iutilisée dans la lecture d'un CD.
La lumière laser est très directive.
2) Calculer la fréquence de la
radiation monochromatique.
f = c / l0 = 3,00 108 / (780 10-9)=3,85 1014 Hz.
3) L'indice du polycarbonate est n =
1,55. Calculer la célérité de l'onde lumineuse dans le CD.
v = c / n =
3,00 108 /1,55 =1,94 108 m/s.
4) En déduire la longueur d'onde l de la lumière dans le
polycarbonate sachant que la fréquence ne dépend pas du milieu traversé.
l
= v / f = l0
/ n = 780/1,55 = 503 nm.
Quand le faisceau laser
frappe une cuvette, une partie du faisceau est
réfléchie par le fond de la cuvette et le reste par le bord car le
diamètre du faisceau est plus grand que la largeur de la cuvette. Ces
ondes réfléchies peuvent interférer.
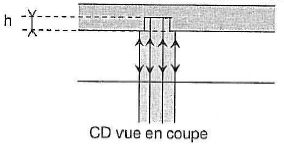
5 a Expliquer pourquoi les
interférences sont destructives si h = 0,25 l.
La différence de marche
entre les ondes réfléchies par le fond de la cuvette et par le bord est
égale à 2 h soit 0,5 l.
les interférences sont
destructives si cette différence de marche est un multiple impair de la
demi-longueur d'onde.
5 b Vérifier que la profondeur d'une
cuvette est bien choisie pour produire des interférences destructives.
0,25 l = 0,25 *503 ~126 nm
= 0,126 µm. Les creux ont une
profondeur h = 0,126 µm.
5 c Comparer sans calcul
l'éclairement de la photodiode quand le faisceau laser éclaire un plat
ou une cuvette.
Lors de la détection
d'un 1, le faisceau laser passe d'un plat à un creux ou inversement.
Une partie du faisceau est alors réfléchie par un plat et l'autre par
un creux. Tous les rayons composant le faisceau n'ont pas parcouru le
même trajet.
Lors de la détection d'un
zéro, le faisceau est entièrement réfléchi par un plat ou par un creux.
Touts les rayons composant le faisceau ont donc parcouru le même
trajet. Les interférences sont constructives et l'éclairement de la
photodiode est maximal.
Lecteur Blu-ray.
On trouve depuis quelques années dans le commerce des lecteurs "
Blu-ray" qui utilisent une diode laser bleue dont la longueur d'onde ( l0
= 405 nm ) est pratiquement égale à la moitié de celle des lecteurs
classiques. Les disques Blu-ray peuvent stocker une quantité de données
beaucoup plus importante : jusqu'à 25 Go.
1)
Quel est le phénomène physique propre aux ondes qui empêche d'obtenir
un faisceau de diamètre plus petit sur le CD ?
La diffraction par un obstacle dont les dimensions sont de l'ordre de
grandeur de la longueur d'onde du faisceau.
2)
Expliquer
pourquoi l'utilisation d'une diode laser bleue peut permettre de
stocker plus d'informations sur un disque Blu-ray dont la surface est
identique à celle d'un CD ?
La finesse de la gravure est de l'ordre de grandeur de la longueur
d'onde et la distance entre deux "rayons" de la spirale est voisine
de deux longueur d'onde. En diminuant celle-ci, on augmente la quantité
de
données gravées.
3) Doit-on conserver sur un disque
Blu-ray, la même profondeur de cuvette que sur un CD classique ?
Justifier.
La profondeur de la gravure doit être égale à 0,25 l : en modifiant la
longueur d'onde de la lumière, on doit changer la profondeur des
cuvettes.
4)
Peut-on lire un CD sur un lecteur Blu-ray ? Une seule justification est
demandée.
Non : la largeur du
faisceau laser et la profondeur des cuvettes sont différentes.
|
|