L'iode radioactif,
phénomènes ondulatoires.
Concours kiné Assas 2016.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
La période radioactive de l'iode 131
est de 8 jours. Il est utilisé comme traceur radioactif ß-.
Son activité spécifique est de 4,6 1015 Bq /g. L'iode
est injecté par voie sanguine ; il se fixe sélectivement sur la
thyroïde. En se désintégrant, il émet des rayons gamma qui peuvent être
détectés par une gamma-caméra.
1. Expliciter la
notion d'isotopes.
Des isotopes ne diffèrent que par leur nombre de neutrons. Ils
possèdent le même numéro atomique Z.
2. La radioactivité de l'iode 131
est-elle naturelle ou artificielle ?
Cet isotope est instable naturellement.
3. Donner la
définition de la période radioactive d'un élément.
La période radioactive est la durée au bout de laquelle l'activité
initiale est divisée par deux.
4. On désire
connaître l'évolution de l'activité A d'un échantillon de 10 mg d'iode
131. Quelle est sa valeur à t = 0. A quoi correspond-t-elle ?
10
mg = 0,010 g ; A0=4,6 1015 *0,010 =4,6 1013
Bq.
L'activité en Bq correspond au nombre de désintégrations par seconde.
5. Quelles sont les activités A1
et A2 de cet échantillon aux dates t1 = 8 jours
et t2 = 32 jours ?
Au bout d'une période ( 8 jours), l'activité initiale a diminué de
moitié : A1 =2,3
1013 Bq.
Au bout de 4 périodes, l'activité initiale a été divisée par 24
= 16 :
A2 =4,6
1013 /16 =2,875 1012 ~2,9 1012 Bq.
6. Ecrire l'équation de désintégration
de l'iode 131. Indiquer les lois utilisées.
13153I
---> 13154Xe
+0-1e + neutrino.
Conservation du nombre de nucléons ( 131 = 131 +0 ) et conservation de
la charge 53 = 54 -1).
7. Calculer
l'énergie libérée E par la désintégration d'un noyau d'iode en joule et
en MeV.
m(13153I ) =130,8770 u ; m( 13154Xe) = 130,8754 u ; m(0-1e) = 0,00055 u.
Dm = m(
13154Xe) +m(0-1e) -m(13153I
) =
130,8754+0,00055-130,8770 =-1,05 10-3 u.
soit -1,05 10-3
*1,66 10-27 =-1,743 10-30 kg
E = Dm
c2 =-1,743
10-30 *9,0 1016 =-1,57 10-13 J.
-1,57 10-13
/ (1,6 10-13) = -0,98 MeV.
Le signe moins traduit le fait que l'énergie est libérée dans le milieu
extérieur.
8. La
désintégration d'un noyau d'iode 131 s'accompagne d'émission g. Quel est la nature de ce
rayonnement ?
Les rayons g sont
des ondes électromagnétiques de même nature que la lumière mais
beaucoup plus énergétiques.
9. Comment peut-on
interpréter l'émission de ce rayonnement ?
Le noyau fils 13154Xe est souvent dans un état excité ; il
revient à un niveau de moindre énergie en émettant des photons gamma.
10. On donne le
diagramme énergétique du noyau fils émis. Calculer la longueur d'onde l
du rayonnement émis correspondant à la transition représentée.
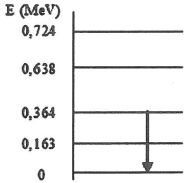
DE
=0,364 MeV = 0,364 *1,6 10-13 =5,824 10-14 J.
l = hc
/ DE= 6,63 10-34 *3,0 108
/ (5,824
10-14)=3,42
10-12 m = 3,42 pm.
|
|
|
Phénomènes ondulatoires.
On réalise une expérience en disposant une source monochromatique de longueur d'onde l devant une fente de largeur a = 0,10 mm. Sur un écran situé à une distance D = 2,00 m, on recueille une figure.
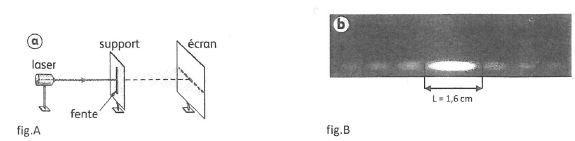
1. Indiquer la propriété des ondes mise en évidence en l'explicitant.
La diffraction met en évidence le caractère ondulatoire de la lumière.
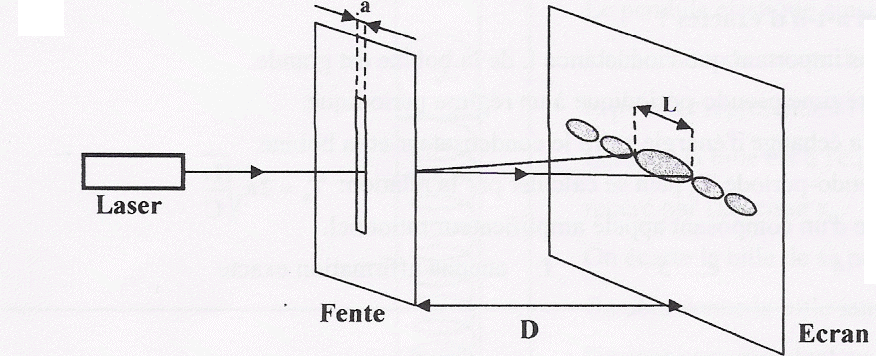
2.
Présenter un schéma de l'expérience en faisant apparaître la largeur de
la fente, la distance fente/écran, la largeur L de la tache centrale et
l'écart angulaire q.
3. Définir l'écart angulaire et donner son expression.
4. Exprimer q en fonction de L et D.
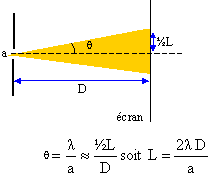
5. En déduire l'expression de la longueur d'onde en fonction de L, D et a.
l = a L / (2D).
6. Calculer cette longueur d'onde. A quelle couleur correspond-t-elle ?
l = 1,0 10-4 *1,6 10-2 / 4,00 =4,0 10-7 m = 400 nm ( limite entre l'UV et le violet ).
|
|
|
|
L'expérience
décrite précédemment est réalisée afin d'estimer le diamètre e d'un
fil. On utilise une nouvelle source monochromatique de longueur d'onde l.
Plusieurs mesures sont effectuées avec des fils d'épaisseur connue. Les
mesures de la largeur L de la tache centrale permettent de tracer les
courbes suivantes.
7. Indiquer en justifiant l'expression correcte de L parmi les propositions suivantes où k est une constante sans dimension.
L est proportionnelle à 1 /a.
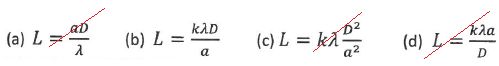
8. Les mesures sont réalisées avec un laser l = 633 nm. Déterminer la valeur de k.
Pente de la droite : 0,104 / (40 103) =2,6 10-6 m2 d'après le graphique.
Pente de la droite d'après l'expression : klD =2,6 10-6 ; k = 2,6 10-6 /(633 10-9 *2,00)=2,0.
9. On place
maintenant le fil d'épaisseur inconnue e entre la source et l'écran. On
suppose la longueur d'onde du laser connue avec exactitude.
La distance vaut D = (2,00 ±0,01 ) m et L =(18 ±1 ) mm.
Donner le résultat du mesurage de l'épaisseur e par cette méthode.
e = 2 lD / L =2*633 10-9 *2,00 / 0,018 = 1,4 10-4 m = 0,14 mm.
[U(e) / e]2 =[U(D) / D]2+ [U(L) / L]2 = [0,01 /2]2+[1/18]2=3,1 10-3.
U(e) / e =5,6 10-2 ; U(e) =5,6 10-2 *0,14 =7,8 10-3 ~1,010-2 mm.
e = (0,14 ± 0,01) mm.
10. Qu'observerait-on en éclairant le fil en lumière blanche ? Expliquer.
L = 2lD/a ; lrouge > l bleue.
La tache centrale est blanche irrisée de rouge.
On remplace la fente par deux fentes de largeur a et distantes de d. La
source utilisée est un laser de longueur d'onde 633 nm. D = 2,00 m. On
observe sur l'écran la figure suivante :

11. Que peut-on dire quant-aux deux ondes en un point lumineux de l'écran ?
12. Interpréter la figure.
Les ondes interfèrent. Dans chaque tache de diffraction, on observe une alternance de zones sombres et brillantes.
13. Donner l'expression de l'interfrange i sachant qu'en un point de l'écran d'abscisse x, la différence de marche est donnée par d = xd / D.
L'interfrange est la distance séparant deux franges consécutives de même nature. Dans le cas des franges brillantes :
xd / D = k l avec k entier.
k = 0, x0 = 0 ; k = 1, x1 = lD / d ; i = x1 - x0 = lD / d.
14. On mesure une distance de 9,5 cm entre 11 franges sombres. Déterminer d.
10 i = 9,5 ; i = 9,5 /10 =0,95 cm = 9,5 10-3 m.
d = lD / i =633 10-9 *2,00 / (9,5 10-3) =1,33 10-4 ~1,3 10-4 m.
15. Comment modifier les fentes si on veut observer sur l'écran un plus grand nombre de franges ?
En diminuant la largeur des fentes, on augmente la largeur de la tache centrale de diffraction.
En augmentant d, on diminue la valeur de l'interfrange.
|
|