oxt
Oxydation des instruments à vent.
Concours interne ingénieurs de l'Industries et des Mines 2016.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Certains
instruments à vent en laiton sont recouverts d'une fine couche d'argent
en surface qui se ternit avec le temps. Ce ternissement est dû à la
présence de H2S dans l'atmosphère qui oxyde l'argent en sulfure d'argent.
A. Produit de solubilité du sulfure d'argent Ag2S.
On fait barboter du sulfure d'hydrogène gazeux dans une solution aqueuse de nitrate d'argennt AgNO3 de concentration 10-2 mol/L de façon à obtenir une concentration constante en H2S dissous de 10-2 mol/L. Il se forme un solide Ag2S selon : 2Ag+ +S2- = Ag2S(s).
A.1. On relève pAg = - log [Ag+]=15,8. Comment peut-on réaliser cette mesure ?
On
immerge un fil d’argent et une électrode au sulfate mercureux (
électrode de référence ) dans la solution de nitrate d'argent.
A.2. On mesure aussi un pH de 2,3. Calculer le produit de solubilité Ks du sulfure d'argent.
Ks = [Ag+]2 [S2-] avec [Ag+] ~1,6 10-16 mol/L.
domaines
de prédominance :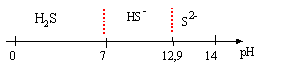
Expression de log[S2-]
en fonction [H3O+]
noté "h" et cs, concentration totale en espèces
soufrées :
H2S+H2O=HS-+H3O+
; ka1 = [HS-][H3O+]/[H2S]
(1)
HS- +H2O=S2-+H3O+
; ka2 = [S2-][H3O+]/[HS-]
(2)
conservation de l'élément soufre : cs
= [H2S]+[HS-]+[S2-]
(3)
solution électriquement neutre : [HS-]+2[S2-]
+[HO-]= [H3O+]
(4)
(1)
s'écrit : [HS-]= ka1[H2S]/[H3O+]
repport dans (2)
: ka2 = [S2-][H3O+]²/(
ka1[H2S]) ; [H2S]=
[S2-][H3O+]²/(
ka1ka2 )
(2)
s'écrit : [HS-] = [S2-][H3O+]/
ka2
repport dans (3)
: cs = [S2-][H3O+]²/(
ka1ka2 ) + [S2-][H3O+]/
ka2 + [S2-]
cs = [S2-]
( 1 + [H3O+]/ ka2
+[H3O+]²/(
ka1ka2 ) )
cs = [S2-]
( 1 + h/ ka2 +h²/( ka1ka2
) )
[S2-]
=cs /(1 + h/ ka2 +h²/( ka1ka2
)).
log [S2-]
= log cs - log (1 + h/ ka2 +h²/(
ka1ka2 )).
cs
= 0,01 mol/L ; log [S2-] = log 0,01 - log (
1+ 1013h + 1020 h²)
si
pH <7 : 1+ 1013h
négligeable devant 1020
h² d'où :
log [S2-]
= log 0,01 - log ( 1020 h²)= -2 -20
-2log h = -22 + 2pH = -22 +2 x2,3 = -17,4 ;
[S2-] ~4 10-18 mol/L.
Ks = [Ag+]2 [S2-]=(1,6 10-16)2 x 4 10-18 = 1,0 10-49.
B. Diagramme potentiel-pH de l'argent dans une solution de sulfures.
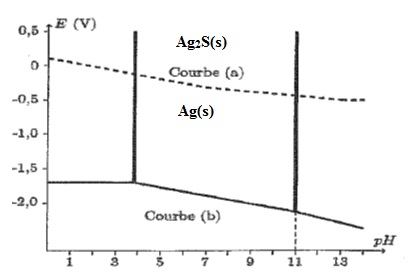 Le
diagramme E=f(pH) de l'argent dans une solution de sulfures est donné
ci-dessus ( courbe a). Il a été tracé pour une concentration en
soufre dissous égale à 10-6 mol/L. Les espèces de l'argent prises en compte sont Ag(s) et Ag2S (s).
Le
diagramme E=f(pH) de l'argent dans une solution de sulfures est donné
ci-dessus ( courbe a). Il a été tracé pour une concentration en
soufre dissous égale à 10-6 mol/L. Les espèces de l'argent prises en compte sont Ag(s) et Ag2S (s).
B.1. Préciser les espèces de prédominance de ces deux espèces.
B.2. Comment expliquer les changement de pente ? Retrouver par le calcul les valeurs numériques des différentes pentes.
Ag(s) =Ag+aq + e-. E = E°(Ag+ /Ag(s) +0,06 log [Ag+].
Ks = [Ag+]2 [S2-] ; [Ag+] = (Ks / [S2-] )½.
E = E°(Ag+ /Ag(s) +0,03 logKs -0,03 log [S2-].
E = 0,8+0,03 x(-49) -0,03 log [S2-].
E = -0,67 -0,03 log [S2-].
A pH <7 : log [S2-]
= log 10-6 - log ( 1020 h²)= -6 -20
-2log h = -26 + 2pH
E = -0,67 -0,03 x(-26)-0,06 pH.
E = 0,11 -0,06 pH.
A pH compris entre 7 et 13 : 1+1020 h² négligeable devant 1013h
d'où :
log [S2-]
= log 10-6- log ( 1013 h)= -6 -13
-log h = -19+pH.
E = -0,67 -0,03 x(-19)-0,03 pH.
E = - 0,10 -0,03 pH.
B.3. Retrouver par le calccul la valeur du potentiel de la zone frontière du couple Ag2S / Ag pour un pH > 13.
.si pH>13 :
1013h + 1020 h²
négligeable devant 1 :
log [S2-]
= log 10-6- log 1 = -6.
E = -0,67 -0,03 x(-6)= - 0,49.
B.4.
En utilisant le diagramme, interpréter l'oxydation de l'argent par le
dioxygène de l'atmosphère sous forme de sulfure
d'argent et écrire la réaction d'oxydoréduction correspondante pour un
pH de l'ordre de 8.
E( Ag2S / Ag ) = -0,10 -0,03 x 8 = -0,34 V.
E(O2 /H2O) = 1,23 V.
Réaction spontanée entre l'oxydant le plus fort ( O2) et le réducteur le plus fort Ag.
Oxydation : 2Ag(s) +S2- = Ag2S + 2e-.
Réduction : ½ O2(g) + 2e- + H2O= 2HO-.
2Ag(s) +S2- +½ O2(g) + H2O= Ag2S + 2HO-.
|
|
|
Traitement des métaux argentés.
D'aucun
l'affirme que l'on peut faire disparaître le sulfure d'argent noir en
faisant chauffer une solution aqueuse de carbonate de sodium Na2CO3
avec l'intrument à traiter dans un récipient en aluminium. Npous allons
vérifier la pertinence de cette affirmation. La réaction est :
3Ag2S(s) +2Al(s) +5HO- +3H2O = 6Ag +3HS- +2Al(OH)4-aq. (R1)
C.1. Calculer l'enthalpie standard DrH° et l'enthalpie libre standard DrG° de cette réaction à 298 K.
DrH°= 2DfH°(Al(OH)4-aq) +3DfH°(HS-)-5 DfH°(HO-)-3DfH°(Ag2S(s))-3DfH°(H2O).
DrH°=2(-1490,3) +3(-17,6) -5(-230)-3(-33)-3(285,2).
DrH°= -2980,6 -52,8 +1150+99+855,6 = -928,8 kJ /mol.
DrS°= 2S°(Al(OH)4-aq) +3S°(HS-)+6S°(Ag)-5 S°(HO-)-3S°(Ag2S(s))-3S°(H2O)-2S°(Al).
DrS°=2x117,2 +3x62,8 +6x42,5-5x10,8-3x144-3x69,9-2x28,3.
DrS°= 234,4 +188,4 +255- 54-432- 209,7 -56,6 = -74,5 J mol-1 K-1.
DrG° =DrH°-TDrS° = -9,288 105 +74,5 T.
C.2.
Donner la valeur numérique de K°, constante d'équilibre de la réaction
à 298 K. Thermodynamiquement, la réaction est-elle favorisée par
une augmentation de la température ?
DrG° =-9,288 105 +74,5 *298 = -9,06 105 J / mol.
DrG° = -RT ln K° ; ln K°= 9,06 105 /(8,314 x298)~365,9. K° ~8,3 10158.
DrH°étant négatif ( réaction exothermique) , la réaction est favorisée par une diminution de la température.
|
|
|
|
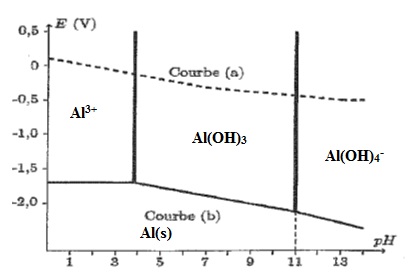
C.3.
Sur le diagramme ci-dessus, figure le diagramme de l'aluminium ( courbe
b). Il est tracé pour une concentration en ion aluminium de 10-2 mol/L. en absence de phase solide. Préciser le domaine de prépondérance de chaque espèce.
C.4. On utilise une solution de carbonate de sodium Na2CO3 de concentration c=0,1 mol/L. Quel est le pH de la solution ?
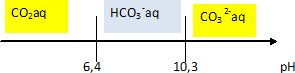
Ka1
= [H3O+][HCO3- ]
/ [CO2aq]
; Ka2
= [H3O+][CO32-]
/[HCO3- ]. Ka1 Ka2
= [H3O+]2 [CO32-] /[CO2aq]
c = [CO2aq] +[HCO3- ] +[CO32-]= 0,1.
Hypothèse [CO2 aq] négligeable devant [HCO3- ] et [CO32-].
|
Avancement volumique
|
CO32-aq
|
+H2O(l)
|
HCO3-aq
|
+HO-aq
|
initial
|
0
|
0,1
|
Solvant
|
0
|
0
|
final
|
x
|
0,1-x
|
x
|
x
|
Ke / Ka2
=[HO- ] [HCO3- ]/ [CO32-] =10-14 /10-10,3= 2 10-4 =x2 / (0,1-x) ;
x2+2 10-4 x - 2 10-5 =0.
Discriminant D =4 10-8+8 10-5 ; D½ = 8,946 10-3 ; x = (-2 10-4 +8,946 10-3) / 2 =4,37 10-3.
[H3O+] = 10-14 / (4,37 10-3)=2,29 10-12 mol / L ;
pH = 11,6.
[CO2aq] = [H3O+][HCO3- ]
/ Ka1 =2,29 10-12 x 4,37 10-3 / 10-6,4 ~2,5 10-8 mol/L. L'hypothèse est bien vérifiée.
C.5. La réacttion R1 est-elle réaliste ? Justifier en utilisant le diagramme E = f(pH).
R1 est réaliste : à pH = 11,6, Al(OH)4-aq et HS-aq prédominent.
C.6. Le potentiel redox standard apparent en présence d'ion HS- en concentration de 1 mol/L pour la demi équation redox :
Ag2S (s) + H3O+ +2e- = 2Ag(s) +HS-aq +H2O vaut E°2 = -0,28 V.
En déduire la valeur de la constante d'équilibre de la réaction K°.
E2 = E°2 + 0,03 log ([H3O+] / [HS- ]).
Al(s) +4HO- aq =Al(OH)4-aq + 3e-.
E1 = E°(Al(OH)4-aq / Al(s)) +0,02 log ([ Al(OH)4-aq ] /[HO-aq]4 ).
A l'équilibre E1 = E2 ; E°2 + 0,03 log ([H3O+] / [HS- ]) = E°(Al(OH)4-aq / Al(s)) +0,02 log ([ Al(OH)4-aq ] /[HO-aq]4 ).
E°2 - E°(Al(OH)4-aq / Al(s)) = 0,01 log ([ Al(OH)4-aq ]2 /[HO-aq]8 )- 0,01 log([H3O+]3 / [HS- ]3).
(-0,28 -(-1,2)) / 0,01 = log ([ Al(OH)4-aq ]2 [HS- ]3/ ([HO-aq]8 [H3O+]3).
92= log ([ Al(OH)4-aq ]2 [HS- ]3/ ([HO-aq]5 (10-14)3) = log (K° / 10-42) = log K° +42
log K° = 50. K° = 1050.
|
|