Influence des
bulles sur les arômes.
Concours général 2016.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
On
souhaite étudier l’influence des bulles sur les arômes perçus par le
dégustateur. On peut supposer que les molécules odorantes, dont
beaucoup ont des propriétés tensio-actives, vont s’accrocher aux bulles
lors de leur ascension, puis être dispersées dans l’air lorsque les
bulles éclateront. L’idée est donc d’analyser la composition chimique
du Champagne au coeur de la flûte et celle des gouttelettes au-dessus
de la surface du liquide, par le biais d’un spectromètre de masse dont
on va d’abord étudier le principe.
a) Principe de la spectrométrie de masse par transformée de Fourier.
Tout spectromètre de masse est composé de plusieurs blocs :
• un système d’introduction de l’échantillon : il peut être introduit
sous forme gazeuse, liquide, solide, ou encore associé à une méthode
séparative telle que la chromatographie ;
• une source d’ionisation : elle consiste à vaporiser les molécules et les ioniser, soit positivement, soit négativement ;
• un analyseur : il sépare les ions en fonction de leur rapport
masse/charge (souvent représenté directement sous la forme m / z avec z
tel que la charge portée par la molécule soit Q = ze avec e la charge
élémentaire) ;
• un détecteur : il permet de retranscrire la séparation des ions et leur proportion.
On
va étudier un système d’analyse basé sur un piège de Penning, encore
appelé cellule ICR (cellule à résonance cyclotronique ionique), qui
consiste à confiner des ions dans une zone restreinte de l’espace grâce
à des champs électriques, puis à appliquer un champ magnétique
Un champ magnétique entraîne sur une particule chargée une force appelée force magnétique de Lorentz dont l’expression est :


70. Quelles sources de champ magnétique connaissez-vous ? Le champ utilisé ici est très intense et vaut B0 = 12,0 ± 0,1 T. Connaissez-vous un dispositif à même de réaliser un tel champ ?
Les aimants artificiels ou naturels, les électroaimants sont des sources de champ magnétique.
Des électroaimants à bobinage ( solénoïde ) mettant en oeuvre des
matériaux supraconducteurs ou utilisant un dispositif de
refroidissement du bobinage, utilisant des renforts mécaniques
extérieurs( lutte contre la pression magnétique) permettent d'atteindre
30 T.
71. En appliquant
la deuxième loi de Newton à l’ion, montrer que la norme de la vitesse
est constante et exprimer la vitesse angulaire wB associée au mouvement circulaire en fonction de B0, e et m / z.
Dans le repère de Frenet écrire la seconde loi de Newton sur l'axe n.
La particule chargée n'est soumise qu'à la force de Lorentz, centripète.
d'où |q|vB0= m v 2/ r avec wB = v /r et |q| = ze.
v = z eB0 r / m = constante pour un ion donné.
wB = z eB0 / m.
72. Que peut-on en déduire pour le mouvement des différents ions issus d’un même prélèvement ?
Le mouvement d'un ion est circulaire uniforme de rayon r = mv / (z eB0).
Le rayon de la trajectoire dépend de la masse et de la charge de l'ion.
Afin de détecter ces ions, on utilise le fait que des particules
chargées, en se déplaçant, induisent un courant électrique, lui-même à
l’origine d’un champ magnétique. Par un dispositif non décrit ici, on
peut récupérer un signal électrique image de l’intensité du champ
magnétique produit : il s’agit pour un ion d’un signal sinusoïdal
amorti faiblement au cours du temps dont la pulsation n’est autre que wB.
|
|
|
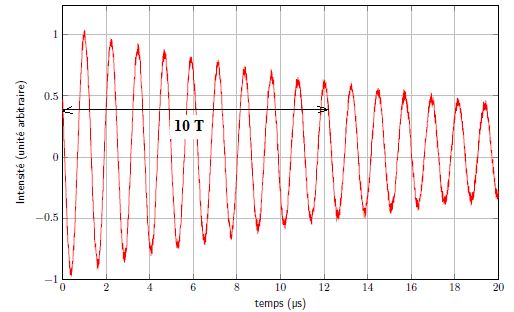
73. Mesurer la période du signal en évaluant l’incertitude.
T = 1,2 ±0,02 µs
74. Après avoir rappelé le lien entre pulsation et période, en déduire la valeur de m /z. On l’exprimera en unité de masse atomique.
wB = 2 p/T ; wB = z eB0 / m ; m / z = e B0 T / (2p).
m / z = 1,6 10-19*12,0 *1,2 10-6 / 6,28 = 3,66 10-25 kg.
3,66 10-25 / (1,661 10-27 )~220,8 u.
75.
Calculer alors l’incertitude-type sur m / z.. Discuter de la valeur
obtenue,à la lueur de la figure 11 représentant un spectre réalisé par
ce type de technique.
[u(m/z) / (m/z)]2 =[u(B0) / B0]2 + [u(T) / T]2 = [0,1 / 12]2 +|0,02/1,2]2 =3,47 10-4 ;
u(m/z) / (m/z) ~2 10-2.
m / z =221 ± 0,02 u.
Cette valeur est peu précise au regard de la précision apportée par la transformée de Fourier.
|
|
|
|
b) Mesures réalisées sur du champagne.
En réalité un grand nombre de ces signaux se superposent au cours du
temps, lorsque l’échantillon à analyser est composé de plusieurs
espèces chimiques. On ne peut plus étudier temporellement le signal
électrique, on a alors recours à la transformée de Fourier, qui permet
à partir d’un signal temporel de remonter à l’ensemble des fréquences
composant un signal et leur importance respective. Après conversion
entre fréquence et m /z, on peut donc représenter une proportion
relative des différents rapports m / z.. Sont représentés ci-dessous
différents résultats selon que l’analyse par spectrométrie de masse a
été effectuée au coeur de la flûte ou au-dessus du liquide.
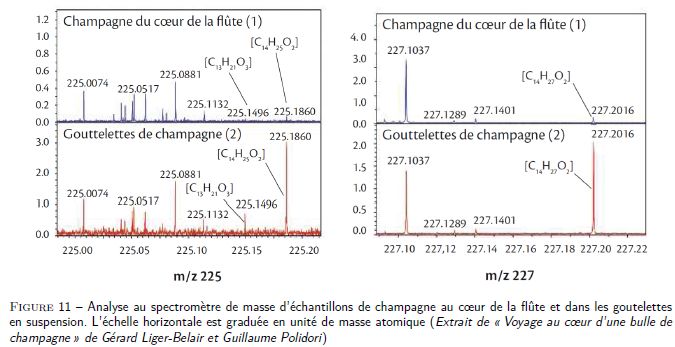
76. Analyser les différents spectres et indiquer les valeurs de m/z dont l’amplitude est particulièrement différente.
m/z = 225 : les pics à 225,1496 et 225,1860 ont des amplitudes très différentes.
m/z = 227 : le pic à 227,2016 a une amplitude très différente.
Ces derniers prédominent dans les gouttelettes de champagne et sont pratiquement absents au coeur de la flûte.
77. A partir des
données suivantes, conclure quant à l’influence des bulles sur les
arômes que l’on est susceptible de capter par l’odorat.
C14H26O2 Acide myristoléique (arôme herbacé)
C13H22O3 Blumenol B (arôme fruité)
C14H28O2 Acide tétradécanoïque (acide gras)
Ces trois arômes sont présents seulement dans les gouttelettes et sont susceptibles d'être capter par l'odorat.
78. Que pourra-t-on
constater qualitativement d’un point de vue olfactif pour un champagne
versé dans une flûte depuis une vingtaine de minutes ?
Un
champagne versé dans une flûte depuis une vingtaine de minutes ne
contient pratiquement plus de bulles de dioxyde de carbone et encore
moins de gouttelettes au dessus du liquide.
|
|
|
|