Ouverture de la
bouteille de champagne.
Concours général SPCL 2016.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Le "Bop !" du champagne.
L'ouverture provoque un son caractéristique, dû notamment à l'évacuation de l'excès de CO2.
27. Donner la définition d'une
onde sonore. La vitesse de propagation d'une onde sonore dans l'air est
de l'ordre de 340 m/s. Qu'en est-il dans les liquides ? Dans les
solides ? Dans le vide ?
Une onde sonore est une onde mécanique longitudinale ( propagation
d'une perturbation dans un milieu matériel ). Il y a transport
d'énergie ; il n'y a pas transport de matière.
Vitesse du son dans un liquide : ~1500 m/s ; dans un solide 4000 à 5000 m/s. Le son ne se propage pas dans le vide.
28.
Le niveau d'intensité sonore de ce "Bop" est de 110 dB lorsqu'il est
perçu à 33 cm de la bouteille, sa fréquence est de 315 Hz. Ce "Bop"
pourra t-il être entendu dans l'appartement au dessus de clelui dans
lequel la bouteille est ouverte sachant que le plafond est assimilable
à une cloison d'indice d'affaiblissement acoustique Rw = 33 dB ? Justifier.
Intensité sonore d'une source isotrope : I = P / (4pd2) avec P : puissance acoustique et d distance du point considéré à la source.
I = I0 1011 =10-12 *1011 = 0,1 W m-2 ; P = 4pd2I=4*3,14*0,332 *0,1 =0,137 W.
Intensité acoustique au niveau du plafond situé à 2 m de la source :
I = 0,137 /(4*3,14*22) ~2,7 10-3 W m-2.
Niveau sonore correspondant : L = 10 log(2,7 10-3) / 10-12)~94 dB.
Affaiblissement dû au plafond : 33 dB ; niveau sonore perçu à l'étage : 94-33 ~61 dB.
Valeur minimale du niveau sonore à 315 Hz : ~15 dB.
Ce "Bop" peut donc être entendu à l'étage supérieur.
29. Ce "Bop" sera t-il audible deux étages au dessus ?
Intensité acoustique au niveau du plafond situé à 5 m de la source :
I = 0,137 /(4*3,14*52) ~4,4 10-4 W m-2.
Niveau sonore correspondant : L = 10 log(4,4 10-4) / 10-12)~86 dB.
Affaiblissement dû aux 2 plafonds : 66 dB ; niveau sonore perçu à l'étage : 86-66 ~20 dB.
Ce "Bop" sera pratiquement inaudible deux étages au-dessus.
Le départ du bouchon.

30.
A l'aide de la séquence d'images et sachant que la longueur d'un
bouchon de champagne est égale à 5,0 cm, estimer la vitesse du bouchon
lors de son éjection. Estimer l'erreur relative à cette méthode de
mesure.
Le bouchon parcourt environ 10 cm en 0,01 s au moment de l'éjection.
Vitesse moyenne de départ :0,10 /0,01 ~10 m /s.
L'erreur est due essentiellement sur la mesure de la distance parcourue 10 ±0,5 cm.
Erreur relative : 0,5 / 10 *100 ~5 %.
31. Proposer une stratégie expérimentale pour diminuer cette incertitude.
Utiliser une caméra qui enregistre un plus grand nombre d'image par seconde.
32. Si la bouteille
est orientée en direction d'un convive, ce dernier entendrat-il le
"Bop" avant ou après être percuté par le bouchon ?
Si le convive se trouve à 1 m, il est percuté 0,1 s après le départ du bouchon.
Le son parcourt 1 m en 1/340 ~0,003 s. Il entend le son avant d'être percuté par le bouchon.
33.
Il est dangereux de se placer à proximité d'un golfeur qui effectue un
swing pour frapper la balle, mais qu'en est-il à proximité d'une
personne qui ouvre une bouteille de champagne ?. On se propose, pour
répondre à cette question, de comparer l'énergie cinétique du bouchon
de champagne lors de son éjection à celle d'une balle de golf de 46 g
frappée lors d'un swing. La chronographie du club de golf, à 100 images
par seconde, est donnée ci-dessous, la longueur visible du club est de
120 cm. Pourquoi s'intéresse t-on à l'énergie cinétique pour répondre au problème posé ?
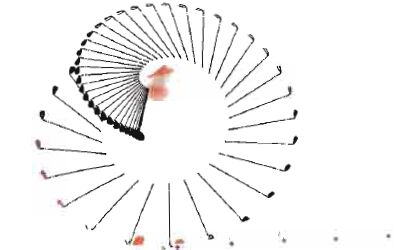
La balle de golf parcourt environ 1,20 m en 0,01 s ; sa vitesse est :1,2 /0,01 = 120 m/s.
Energie cinétique du bouchon : ½mv2 = 0,5 *0,010*102 =0,5 J.
Energie cinétique de la balle : 0,5*0,046*1202 ~300 J. C'est 600 fois plus dangereux que l'éjection du bouchon.
Lors de l'impact, l'énergie cinétique est convertie en chaleur et en déformation de la cible.
34. En négligeant les frottement subis par le bouchon au cours de son
mouvement dans l'air, déterminer la hauteur maximale atteinte.
La conservation de l'énergie mécanique du bouchon donne : h = v2 / (2g) ~ 102 / 20 ~ 5 m.
|
|
|
Le rafraîchissement du champagne.
Le seau à champagne ou le réfrigérateur.
Une bouteille de champagne, initialement à 12°C, est plongée dans le
seau à champagne contenant 4 L d'eau à 2°C. En première approximation
on peut considéré le seau comme une enceinte adiabatique ( pas de
transfert thermique entre le seau et l'extérieur).
Capacité thermique massique : Cvin = 4185 J K-1 kg-1 ; Cverre = 720 J K-1 kg-1 ; masse d'une bouteille de champagne vide m = 1,1 kg.
35. Vérifier par le calcul que la température du champagne est d'environ 4 °C à l'équilibre thermique.
Energie gagnée par le vin et la bouteille en verre : Q = (Cvin mvin +mverre Cverre ) ( qfin-qini).
Q =(4185*0,75 +1,1*720) ( qfin-12) = 3,93 103qfin -4,7 104 J.
Energie cédée par l'eau du seau : Q' = Ceau meau ( qfin-q0).
Q' = 4185*4( qfin-2) = 1,67 104qfin -3,35 104 J.
Le système {seau +eau + bouteill + vin} est adiabatique : Q+Q'=0.
1,67 104qfin -3,35 104 +3,93 103qfin -4,7 104 =0.
2,07 104qfin =8,05 104 ; qfin =3,9°C ~4°C.
36.
La même bouteille de champagne, initialement à 12°C est placée dans un
réfrigérateur de puissance 300 W et dont l'efficacité énergétique est
de 20 %. Déterminer le temps nécessaire pour que la bouteille atteigne
4°C.
|Q| = -3,93 103*4 +4,7 104 =3,1 104 J.
t = 3,1 104 / (300*0,2) ~510 s ~ 8,6 min.
|
|
|
|
Détente du gaz à l'ouverture de la bouteille.
A
l'ouverture de la bouteille, les 2,5 cL de gaz comprimé entre le
liquide et le bouchon à une pression de 6 bar subissent une détente
adiabatique, c'est à dire que le gaz voit sa pression diminuer jusqu'à
une pression égale à la pression atmosphérique, sans échan,ger
d'énergie sous forme de chaleur avec l'extérieur. Le gaz constitué de
différentes espèces chimiques dont le dioxyde de carbone, sera
considéré comme parfait. Au cours de la transformation que l'on
considère comme réversible, on a la relation PVg = constante avec P pression du gaz, V volume du gaz et g = 1,3 pour le gaz étudié.
37. Déterminer le volume du gaz après détente.
Pf Vfg = Pi Vig ; Vf =Vi (Pi /Pf)1/g = 2,5 *61/1,3 =9,9 cL.
38. On considère le gaz initialement à 4°C. Déterminer la vaeur de la température du gaz libéré après cette détente.
n = Pi Vi / (RTi) =Pf Vf / (RTf).
Tf = Pf Vf Ti / (PiVi)=9,9 *277 /(6*2,5)=183 K ( 183-273 = -90°C).
Au moment de l'ouverture de la bouteille, la détente du gaz comprimé dans la bouteille accentue la sensation de froid.
|
|
|
|