Etude
de fonction.
Concours Geipi Polytech 2016.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Partie A.
On
considère la fonction g définie par pour tout réel x, g(x) = ex-x.
A.1.
g' désigne la dérivée de g. Donner, pour tout réel x, g'(x).
g'(x)
= ex-1.
A.2. Donner
l'ensemble des solutions réelles de l'inéquation g'(x) supérieur ou
égal à zéro. Justifier.
ex >= 1 ; ln(ex)
>= ln 1 ; x >= ln 1 ; x >=0.
A.3. Dresser le
tableau des variations de g.
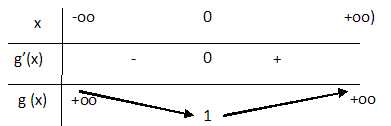
A.43.
Justifier que, pour tout réel x, g(x) >0.
Pour
tout réel x, g(x) > g(0) ; or g(0) = 1 ; donc g(x) >0.
Partie B.
On considère la fonction f définie par :
pour tout réel x, f(x) = ex / (ex-x).
On note C la courbe représentative de f dans le plan rapporté à un
repère orthonormé.
B.1.a.
Déterminer la limite de f(x) quand x tend vers moins l'infini.
Quand x tend vers moins l'infini, ex tend vers
zéro, donc f(x) tend vers zéro.
x
/ ex tend vers zéro lorsque x tend vers l'infini.
f(x) tend vers 1 lorsque x tend vers l'infini.
B.1.b Déterminer la limite de f(x) quand x
tend vers l'infini.
f(x) = 1 / [1 -x /
ex].
x
/ ex tend vers zéro lorsque x tend vers l'infini.
f(x) tend vers 1 lorsque x tend vers l'infini.
B.1.c.
On en déduit que C admet deux asymptotes D1
et D2.
Donner une équation de chacune d'ellles.
Quand x tend vers l'infini, la droite d'équation y = 1 est asymptote.
Quand
x tend vers moins l'infini, la droite d'équation y = 0 est asymptote.
B.2.
f' désigne la dérivée de f. Justifier que, pour tout réel x, f '(x)= ex(1-x)
/ (ex-x)2.
On pose u = ex ; u' = ex.
v = (ex-x) ; v' = ex-1.
Dérivée d'un quotient : f ' = (u'v-v'u) / v2.
f ' =[ ( ex
(ex-x)) - (
ex-1)ex
] / (ex-x)2=
ex(1-x) / (ex-x)2.
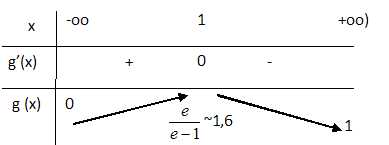
B.3.
Dresser le tableau de variation de f. Donner les valeurs exactes du
maximum yM atteint pour xM.
On note M le pont de coordonnées (xM, yM).
|
|
|
B.4. Soit A le point
de la courbe C d'abscisse 0. Donner une équation de la tangente à C en
A.
A( 0 ; 1) ; f '0) = 1 ; équation de la tangente à la courbe C en A :
y = f '(0) x+ b = x+b ; yA = xA+b
d'où b = 1 soit y = x+1.
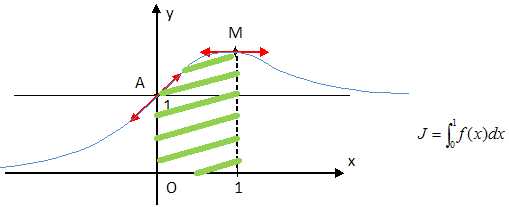
B.5.
Placer les points A et M.Tracer les tangentes à la courbe C au points A
et M et les asymptotes. Puis tracer C.
B.6.
f admet sur l'intervalle [0 ; 1] un minimum a et un maximum b. Donner
les valeurs exactes de a et b.
a = f(0) = 1 ; b = f(1) = e / (1-e).
2,86 106 / (890 103) =3,2
mol.
Le monoxyde de carbone produit par le reformage est un poison pour le
catalyseur. Il faut donc l’oxyder intégralement en dioxyde de carbone
au fur et à mesure de sa formation.
B.7.
On considère l'intégrale J. Hachurer sur la figure le domaine dont
l'aire, en unités d'aire, vaut J. Justifier que 1<= J<= e
/ (e-1).
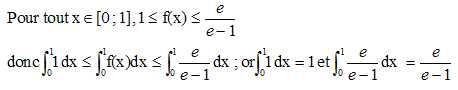
|
|
|
|
On considère la fonction f définie par : pour tout xappartenant à ]0 ; +oo[, f(x) =(2 ln x-1) / x.
On note Cf la courbe représentative de f dans le plan rapporté à un repère orthogonal.
II-1-a- Donner la limite de f(x) quand x tend vers zéro.
f(x) tend vers moins l'infini quand x tend vers zéro.
II-1-b- Que vaut la limite de ln x / x quand x tend vers l'infini ? En déduire la limite de f(x) quand x tend vers l'infini. Justifier.
Ln x / x tend vers zéro quand x tend vers l'infini.
f(x) = 2 ln x / x -1 / x.
1 / x tend vers zéro quand x tend vers l'infini. Donc f(x) tend vers zéro quand x tend vers l'infini.
II-1-c- On en déduit que Cf admet deux asymptotes. Donner une équation de chacune d’elles.
x = 0, asymptote verticale ; y=0 asymptote horizontale.
II-2- f ' désigne la dérivée de f. Justifier que : pour tout x appartenant à ]0; +oo1[, f '(x) =(3-2lnx) / x2.
On pose u = 2lnx -1 et v = x.
u' = 2 /x et v' = 1 ; dérivée d'un quotient :
(u'v-v'u) / v2 = .(2 -(2lnx -1)) / x2 = (3-2lnx) / x2.
II-3-a- Dresser le tableau des variations de f.
II-3-b- La fonction f présente un maximum yM atteint en xM.
Donner les valeurs exactes puis des valeurs approchées à 10−1 près de xM et yM.
Dans la suite, on note M le point de coordonnées (xM, yM).
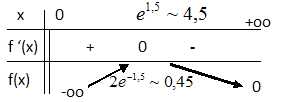
II-4-a- Donner les valeurs de f(1) et f '(1).
f(1) = -1 ; f '(1) = 3.
II-4-b- Soit A le point de la courbe Cf d’abscisse 1 et T la tangente à Cf au point A. Donner une équation de T.
y = a x +b avec a = f '(1)= 3 et b = f(1)- a = -1 -3 = -4 ; y = 3x-4.
II-5- Soit B le point d’intersection de la courbe Cf et de l’axe des abscisses. On note (xB, yB) ses coordonnées.
Donner les valeurs exactes de xB et de yB, puis une valeur approchée de xB à 10−1 près.
yB = 0 ; 2 ln xB = 1 ; xB = e0,5~1,6.
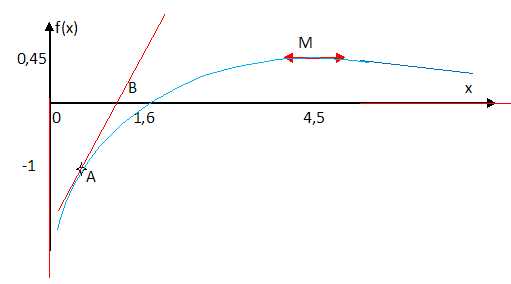
II-6- Placer les points A, B et M.
Tracer les tangentes à la courbe Cf aux points A et M et les asymptotes. Puis tracer C.
|
|