Thermique,
éolienne, fourche optique, iode 131. Concours Geipi 2016.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Thermique.
L'industrie agroalimentaire utilise souvent la vapeur d'eau pour
dégraisser, nettoyer ou désinfecter. On souhaite produire de la vapeur
d'eau à 180 °C sous une pression de 5 bar. Pour cela, on amène de l'eau
liquide à 20 °C dans une cuve à 180 °C où règne une pression constante
de 5 bar. La source d'énergie utilisée est le méthane CH4.
Données
:
Masse volumique de l’eau liquide r =
1,00 kg. L-1 ;
capacité thermique massique de l’eau liquide Ceau(l)
= 4,18 kJ.kg-1.K-1 ;
capacité thermique massique de la vapeur d'eau à la pression de 5 bar Ceau(v)
= 2,01 kJ.kg-1.K-1 ;
capacité thermique massique de l’eau solide Ceau(s)
= 2,06 kJ.kg-1.K-1.
Chaleur latente de vaporisation de l’eau à la température q eb
Lvap = 2100 kJ.kg-1.
Les calculs suivants seront effectués pour un système constitué d'une
masse m = 1 kg d'eau.
I-1-
Calculer le nombre de moles présentes dans le système.
n = 1000 /18 = 55,6 mol.
I-2-
Donner l'unité de la constante R des gaz parfait. (On rappelle que la
relation des gaz
parfait s'écrit p V=n R T avec R = 8,314 SI).
J K-1 mol-1.
I-3-
En faisant l'hypothèse que la vapeur d'eau se comporte comme un gaz
parfait, quel volume occupe 1 kg de vapeur d'eau dans les conditions
(p=5 bar, q2
=180 °C) ?
V = nRT /p = 55,6 *8,314*(273+180) / (5 105) =
0,418 ~0,42 m3.
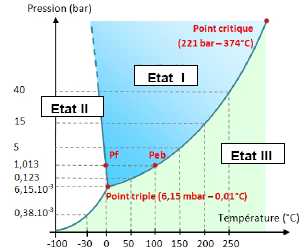
I-4- Sur le
diagramme (p, q)
de l'eau ci-dessus, à quoi correspondent les 3 états de la matière I,
II et III.
Etat I : liquide ; état II : solide ; état III : gaz.
Dans la cuve, le système évolue d'un état A (p = 5 bar, q1
= 20 °C) jusqu'à un état B (p = 5 bar,
q2
= 180 °C).
I-5-
A quelle température qeb
aura lieu l'ébullition de l'eau dans la cuve ?
D'après le graphe, qeb = 150°C.
I-6- Donner
l'expression de l’énergie Q1 nécessaire au
chauffage du système de q1
jusqu’à qeb.
Calculer Q1.
Q1 = mCeau(l)
(qeb
-q1 )=1*4,18(150-20)=543,4 ~5,4 102 kJ.
I-7- Calculer
l’énergie Q2 nécessaire à l'évaporation du
système.
Q2 = Lvap
= 2100 kJ.
I-8- Calculer
l’énergie Q3 nécessaire au chauffage du système
de qeb
jusqu'à q2.
Q3
= mCeau(v)
(q2
-qEb )=1*2,01(180-150)=60,3 kJ.
I-9- Calculer
l’énergie thermique nécessaire pour passer le système de l'état A à
l'état B.
543,4 + 2100 + 60,3 = 2703,7 ~2,7
103 kJ.
I-10-
Compléter la chaîne énergétique du document réponse.
Energie chimique ---> Combustion du méthane --- nergie thermique.
I-11-
En pratique, on mesure une consommation de 4030 kJ. En déduire le
rendement thermique de ce processus de chauffage.
2703,7 / 4030 = 0,67 ( 67
%).
I-12- La combustion
d’une mole de méthane libère une énergie de 803 kJ dans les conditions
de l'expérience. Quelle masse de méthane faudrait-il utiliser pour
produire 1 kg de vapeur ?
n(méthane) = 4030 / 803 =5,02 mol ;
m = n(méthane) * M(méthane) = 5,02 *16,0 =80,3 g.
I-13-
Donner les noms des produits de la combustion complète du méthane dans
le dioxygène de l'air. En déduire l'équation bilan équilibrée de cette
réaction.
CH4 + 2O2 --> CO2
+ 2H2O.
I-14-
Quelle est la masse de dioxygène nécessaire à cette combustion ?
n(O2) = 2 n(méthane) =~10,0 mol ; n(O2)M(O2
= 10,0 *32 = 320
g.
|
|
|
Aérogénérateur.
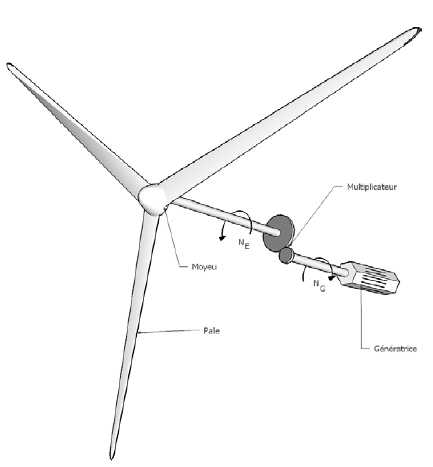
On envisage l’étude d’un aérogénérateur composé :
- d’une éolienne comportant trois pâles de longueur L = 38 m
(fixées sur un moyeu (de diamètre
négligeable par rapport à L),
- d’un multiplicateur planétaire permet d’accroître la vitesse
de rotation de l’arbre de l’éolienne NE
pour l’adapter à celle de la génératrice NG,
- d’une génératrice électrique asynchrone.
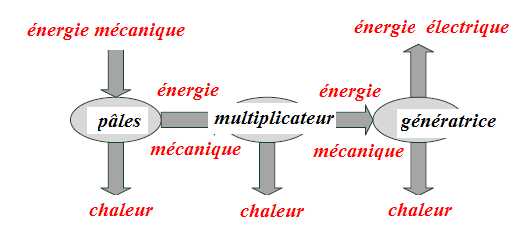
II-1- Compléter la
chaîne énergétique illustrant la conversion d’énergie en portant sur
les flèches le type d’énergie impliqué (mécanique, électrique, chaleur).
II-2-
Déterminer l’expression littérale et la valeur numérique de la surface
S balayée par les pâles en rotation.
S=pL2
= 3,14 *382 = 4536 ~4,5 103 m2.
II-3-
On assimile l’air à un fluide incompressible de densité r =
1,22 kg.m-3 se déplaçant à une vitesse V = 10 m.s-1
sous l’effet du vent. La masse d’air mA
traversant la surface S pendant un intervalle de temps Dt est
égale à mA= S. r.V.Dt.
Contrôler la validité de cette expression grâce à l'analyse
dimensionnelle.
[S]=L2 ; [r]=ML-3]
; [V]=L
T -1 ; [Dt]= T ; [mA]= M.
II-4- Donner
l'expression de l’énergie cinétique EA portée
par la masse d’air mA lors de la traversée des
pâles.
EA = ½mA V2.
II-5-
Déduire de la question précédente l'expression de la puissance associée
en fonction de
V,S et r.
Calculer PA.
PA = EA / Dt = ½ S. r. V3.
PA = 0,5 *4536 1,22 *103
= 2,78 106 W.
II-6- La puissance
mécanique exploitable par l’éolienne est mesurée à PM
=1328 kW. Elle est
inférieure à la puissance PA . Expliquer
l’origine physique de cette perte d’énergie et déterminer
le rendement de la conversion d’énergie mécanique par l’éolienne noté hE.
L'éolienne freine l'écoulement d'air, sans l'arrêter. L'air possède
encore de l'énergie cinétique après avoir traversé l'éolienne.
hE
= 1328 /(2,78 103 )=0,477 ~0,48.
II-7- Le rendement
énergétique du multiplicateur étant hM
= 80%, et celui de la génératrice de
hG=95%.
Déterminer la puissance PG récupérée en sortie
de génératrice.
PG = PM hMhG= 1328*0,80*0,95 ~1,0 103 kW.
II-8-
Le coefficient de vitesse spécifique l
d’une l’éolienne est défini comme le rapport entre la vitesse de
l’extrémité d’une pale et la vitesse du vent. En déduire la relation
entre la vitesse de rotation de l’éolienne NE
(en tr/min) et celle du vent V (en m.s-1).
l
= 2pNE
L / (60V) ; NE
= 60V l / (2pL).
II-9-
L’éolienne étudiée possède un l=7,46.
En déduire NE (en tr/min). Quel doit être alors
le rapport de multiplication k = NG/NE
pour obtenir une vitesse NG=1500 tr/min ?
NE = 60*10*7,46 /(2*3,14*38)=18,76 ~ 19 tr/min ;
k = 1500 /18,76 ~80.
II-10-
Enumérer les deux principaux avantages et inconvénients de la
production éolienne d’électricité.
Avantages : énergie renouvelable,pas d'émission de dioxyde de carbone.
Inconvénients : production intermittente, contrainte environnementale (
visuel, bruit )
|
|
|
|
Fourche optique.
Une fourche optique est un capteur constituée
d’un dispositif d’émission de lumière infrarouge (LED) et de réception
(phototransistor) placés en vis à vis. Une roue dentée (N = 30 dents)
solidaire de l’arbre moteur est partiellement insérée dans la fourche
optique.
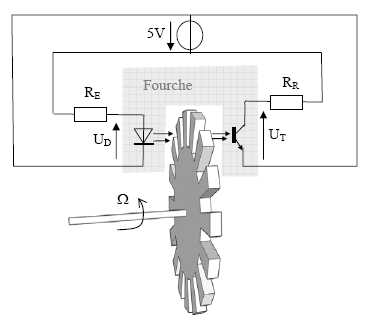
III-1-
Quelles sont les grandeurs d’entrée et de sortie de la fourche optique ?
Entrée : position de la fourche ; sortie : tension.
III-2-
Comment qualifier ce capteur ?
Capteur actif, tout ou rien ( TOR).
III-3-
La tension aux bornes de la LED est UD = 1,2 V.
Déterminer la valeur de RE permettant
l’établissement un courant d’intensité 10 mA dans le circuit d’émission
de lumière.
RE = (5-1,2) / 0,010 = 3,8 102 ohms.
On considère que le phototransistor fonctionne comme un interrupteur :
- fermé quand il reçoit de la lumière
- ouvert quand il ne reçoit pas de lumière
III-4-
Donner la valeur de la tension UT lorsque le
phototransistor reçoit et ne reçoit pas le faisceau de lumière
infrarouge.
Lumière reçue : UT = 0 ; pas de lumière : UT
= 5 V.
III-5-
Expliquer quelle est la fonction de la résistance RR
dans le circuit de réception ?
Protection du phototransistor contre les surintensités.
III-6-
En considérant la vitesse de rotation de la roue constante pendant un
tour, justifier le caractère périodique de UT.
Le faisceau de la LED est occulté de manière périodique lors de la
rotation de la roue.
III-7-
Exprimer la période T(en s) de UT en fonction de
W,
vitesse de rotation du moteur (exprimée en tr/mn) et de N.
T = 60 / (NW).
On souhaite utiliser le système précédant pour effectuer la mesure de
la vitesse de rotation W.
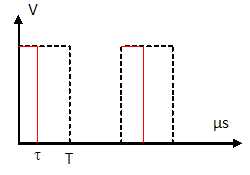
Le signal UT est envoyé sur un dispositif
électronique (non représentée sur la figure) qui génère une tension Um
sous la forme d’une impulsion positive d’amplitude 5V et de durée t≤T
sur chaque front montant de UT.
III-8-
Sur le document réponse où est déjà représenté le signal UT,
tracer l’évolution de la tension de sortie du monostable Um
au cours du temps.
III-9-
Soit Wmax=6000
tr/min la vitesse maximale du moteur, déterminer la contrainte sur t pour
pouvoir effectuer la mesure.
t
doit être inférieur ou égal à : 60 /(NW) =
60 /(30*6000) =3,3 10-4 s.
III-10-
Etablir l’expression de la valeur moyenne de la tension Um
sous la forme <Um> = KW.
<Um>
=5 t
/ T = 5t N / 60 W.
Déterminer
l’expression littérale puis la valeur numérique de K assortie d’une
unité avec t
=100 µs
K = = 5t N /
60 =5 * 100 10-6 *30 /60 =2,5 10-4 V min tr-1.
|
Iode 131.
Après usage dans les hôpitaux, les produits radioactifs doivent être
collectés. Selon la réglementation, leur traitement est effectué au
sein de l’hôpital si la valeur de leur période radioactive, ou temps de
demi-vie, t½ est inférieure à 71 jours. Au-delà,
ils doivent être confiés à un organisme spécialisé dans le traitement
des déchets.
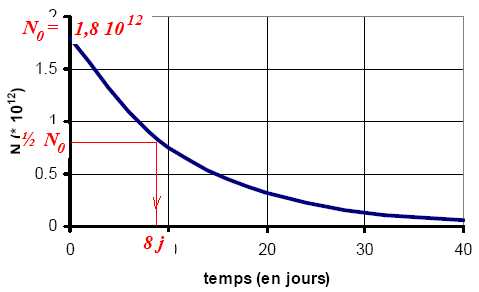
La figure1 ci-dessous représente l'évolution temporelle d'une dose
d'iode 131 utilisée en médecine pour l'examen par scintigraphie de la
thyroïde.
Le nombre de noyaux évolue en suivant une loi de décroissance
exponentielle : N(t) = N0 exp(-lt).
N0 est le nombre de noyaux à l’instant initial
et l
la constante radioactive .
VI-1-
En utilisant la figure1, déterminer la valeur du temps de demi-vie t½
de l'échantillon l'iode 131 ainsi que le nombre initial de noyaux
radioactifs N0.
VI-2-
Démontrer que t½ = ln2 / l. En
déduire la valeur de l
dans le système d'unité international.
N(t½) = 0,5 N0 = N0
exp(-lt½)
; 0,5 = exp(-lt½)
; ln 0,5 = -ln 2 = -lt½.
l
= ln2 / 8 = 8,7 10-2
j-1 ou ln2 /(8*24*3600) =1,0 10-6 s-1.
VI-3-
Donner l'unité de l'activité radioactive. Calculer l'activité moyenne
de cet échantillon entre 0 et 10 jours.
L'activité s'exprime en bequerel ( Bq).
A0 = lN0
= 1,0 10-6 *1,8 1012 =
1,8 106 Bq.
A10 =A0 exp(-10l)
= 1,8 106 exp(-0,87)=7,5 105
Bq.
Activité moyenne : (1,8 106 +7,5 105
) /2 ~1,3 106 Bq.
VI-4-
Combien restera-t-il d'atomes d'iode radioactifs au bout d'une durée de
71 jours ?
N = N0 exp(-71l )=
1,8 1012 exp(-71*0,087) =3,8 109.
VI-5-
L'échantillon d’iode peut-il être retraité dans l’hôpital ou doit-il
être retraité par un intervenant extérieur ? Justifier.
A l'hopital, lademi-vie est inférieure à 71 jours.
La réaction de désintégration majoritaire de l'iode 131 s'écrit
13153I--->
13154Xe +0-1e.
VI-6-
Préciser la composition du noyau de l'iode 131.
53 protons et 131-53 = 78 neutrons.
VI-7-
Parmi les noyaux proposés dans le document réponse, sélectionner le ou
les isotopes de l'iode 131.
12353I et 12753I.
VI-8-
La désintégration de iode 131 est-elle de type a, ß-
, ß+ ou g ?
Radioactivité de type ß- suivie d'émission g.
Le Xénon produit n'est pas stable, sa réaction de
désexcitation s'écrit Xe* --> Xe +g.
VI-9-
Quelle est la nature de la particule g ?
Photon de haute énergie.
VI-10-
Préciser le numéro atomique Z et le nombre de masse A du noyau de Xénon
obtenu après la réaction de désexcitation. 13154Xe.
|
|