Canon
à électrons.
Concours Geipi Polytech 2016.
|
|
.
.
|
|
|
|
|
|
|
|
Dans
les domaines de la science des matériaux, on a souvent recourt à un
microscope haute
résolution pour étudier leur microstructure. L’augmentation de la
résolution passant par une
diminution de la longueur d’onde, on utilise un faisceau d’électrons à
la place d’un faisceau de
photons visibles. Dans un microscope électronique à balayage, les
électrons sont accélérés grâce
à un champ électrique produit par une différence de potentiel entre la
source et une anode, puis
focalisés sur l'échantillon par des lentilles magnétiques ou
électrostatiques. Après interaction avec
l'échantillon, le faisceau d'électrons est mesuré par un détecteur
permettant de former une image
du cristal. On se propose d’étudier ici le canon à électrons qui
accélère les électrons d’une plaque
A vers une plaque B.
Le champ électrique E est uniforme et horizontal entre les plaques A et B verticales. Sa norme vaut : E = 300 000 V.m-1.
On étudie le mouvement d’un électron de masse m et de charge – e entre ces deux plaques.
Au temps t = 0, l’électron se trouve en O, origine du repère cartésien.
La vitesse de l’électron en O est nulle. L’électron atteint la plaque B
en un point M.
La distance entre les plaques vaut OM = L = 10 cm.
On précise qu’on ne fera pas de corrections relativistes dans tout l’exercice.
Données :
- charge élémentaire e = 1,60*10-19 C ; - intensité de la pesanteur : g = 9,81 m.s-2 ;
- masse de l’électron : m = 9,11*10-31 kg ; - constante de Planck : h = 6,63*10-34 J.s.
Calcul de la vitesse de l’électron par la deuxième loi de Newton.
III-1- Donner l’expression vectorielle de la force électrostatique subie par l’électron en fonction
de E et e. Calculer la norme de cette force.
III-2- Donner l’expression vectorielle du poids de l’électron. Calculer la norme de cette force.
Dans la suite de l’exercice, on décide de négliger le poids de l’électron par rapport à la force
électrostatique.
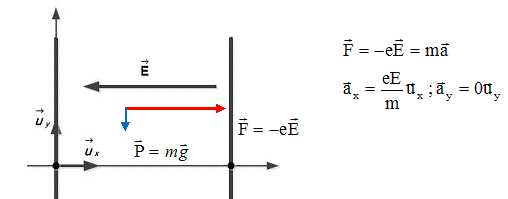
F = 1,60 10-19 *300 000 = 4,80 10-14 N.
P = m g = 9,11 10-31*9,81 = 8,94 10-30 N.
III-3- Appliquer la 2e loi de Newton à l’électron et donner les composantes de l’accélération
suivant x et y. En déduire l’expression des composantes de la vitesse de l’électron en fonction du
temps puis les expressions des composantes de la position de l’électron en fonction du temps.
vx = eE / m t ; vy=0. x = ½eE/m t2.
III-4- En déduire l’expression du temps tM au bout duquel l’électron parviendra à la plaque B.
Faire le calcul.
L = ½eE/m tM2 ; tM =[ 2mL / (eE)]½.
tM = [2*9,11 10-31*0,10 / (1,60 10-19*300 000)]½ =1,95 10-9 ~1,9 10-9 s.
III-5- Calculer la vitesse vM atteinte par l’électron au point M.
vM = eE/m tM =1,60 10-19*300 000 / (9,11 10-31) *1,95 10-9 ~1,0 108 m/s.
|
|
|
Calcul de la vitesse de l’électron par une méthode énergétique.
III-6- Donner l’expression du travail W que fournit la force électrostatique lors du déplacement
de l’électron de 0 vers M, en fonction de E.
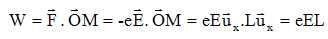
III-7- En définissant la variation d’énergie potentielle électrostatique ΔEp entre O et M par ΔEp = - W et l’énergie potentielle associée à une charge q par Ep = q V, déterminer l’expression
de la différence de potentiel VB-VA appliquée entre les plaques du canon à électron. Faire
l’application numérique.
ΔEp = Ep B-Ep AO = -e(VB-VA) = -eEL ; VB-VA =EL.
VB-VA= 300 000 *0,10 = 3,0 104 V.
On fixe le potentiel VA à zéro volt.
III-8- Donner l’expression de l’énergie mécanique de l’électron en O et calculer sa valeur.
EM = ½mv2O + Ep(A ) = 0.
III-9- Que vaut EM(M) ? Justifier.
La force électrique est une force conservative. Entre O et M, l'énergie mécanique reste constante.
Il n'y a pas dissipation d'énergie par les frottements.
EM(M) =0.
III-10 Donner l’expression de l’énergie mécanique EM(M) de l’électron en M en fonction de vM .
EM(M) = ½mv2M + Ep(B ) = ½mv2M -eVB = 0.
|
|
|
|
III-11- En déduire l’expression de la norme de la vitesse vM de l’électron en M en fonction du potentiel VB.
½mv2M =eVB ; vM = [2eVB/m]½.
Diffraction des électrons.
Après interaction avec la matière, ces électrons perdent un peu d’énergie, leur vitesse vaut désormais v = 8,47*106 m.s-1.
III-12- Enoncer la relation de De Broglie liant la longueur d’onde l associée à une particule et sa quantité de mouvement p.
l = h / p.
III-13- En déduire la valeur de la longueur d’onde des électrons.
l = h / (mv) = 6,63 10-34 /(9,11 10-31*8,47 106) =8,59 10-11 m = 85,9 pm.
III-14- Justifier alors que ces électrons puissent être diffractés par le cristal.
Les
dimensions d'un cristal sont de l'ordre d'une centaine de picomètres,
c'est à dire du même ordre de grandeur que la longueur d'onde des
électrons. Un cristal diffracte donc le faisceau d'électrons.
|
|